Файл: Федеральное агентство связи фгбоу во сибгути.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 22

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Федеральное агентство связи

ФГБОУ ВО СибГУТИ

Кафедра СМС

Расчётно-графическое задание

по дисциплине «Распространение радиоволн и антенно-фидерные устройства»

Выполнил:

студент 3 курса

факультета МРМ гр. РМ-33

Каменев В.К.

Проверил:

Трубехин Е.Р.
Новосибирск 2016

Задание №1. Панельные антенны

Исходные данные:

Номер варианта: 5

Центральная частота диапазона 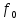= 800 МГц

Поляризация: горизонтальная

Количество полуволновых вибраторов 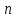= 16

Отношение радиуса вибратора к длине плеча 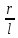= 0,05
Пункт 1.
Длина волны на центральной частоте диапазона:

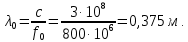
Расстояние до рефлектора:

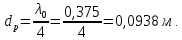
Шаг решётки:

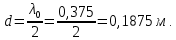
Вертикальный размер антенны:

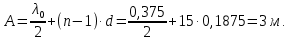
Горизонтальный размер антенны:

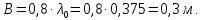
Высота диэлектрического защитного кожуха антенны:


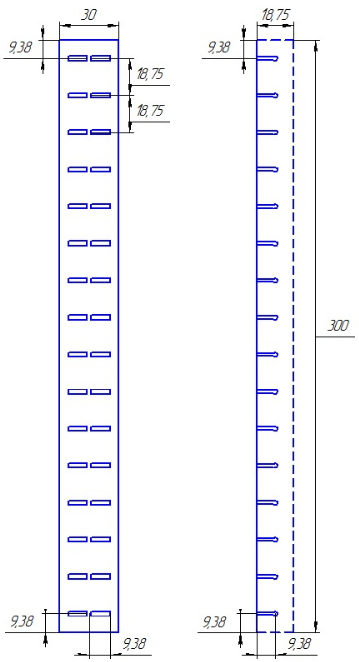
Рисунок 1 – Эскиз панельной антенны с горизонтальной поляризацией
Пункт 2.

В горизонтальной плоскости ДН определяется следующим выражением:



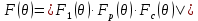
Нормированная ДН симметричного вибратора для антенны с горизонтальной поляризацией:



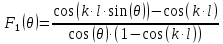
Множитель рефлектора:



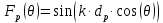
Множитель решётки:



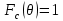
где 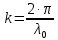– волновое число; 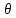– угол в горизонтальной плоскости, отсчитываемый от нормали к защитному корпусу антенны.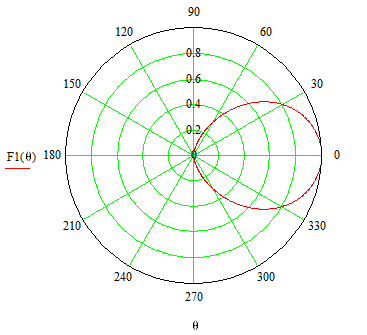



Рисунок 2 – Диаграмма направленности антенны по напряжённости электрического поля в горизонтальной плоскости

В вертикальной плоскости ДН определяется следующим выражением:



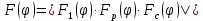
Нормированная ДН симметричного вибратора для антенны с горизонтальной поляризацией:



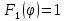
Множитель рефлектора:



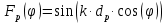
Множитель решётки:



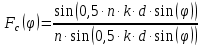
Где – волновое число; 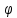– угол в вертикальной плоскости, отсчитываемый от нормали к защитному корпусу антенны.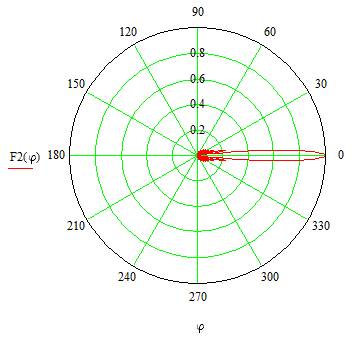



Рисунок 3 – Диаграмма направленности антенны по напряжённости электрического поля в вертикальной плоскости

Пункт 3.

Диаграмма направленности по мощности в горизонтальной плоскости:





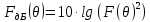
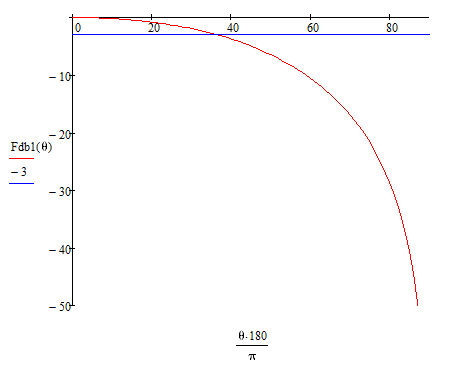
Рисунок 4 - Диаграмма направленности антенны по мощности электрического поля в горизонтальной плоскости

Диаграмма направленности по мощности в вертикальной плоскости:





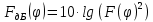
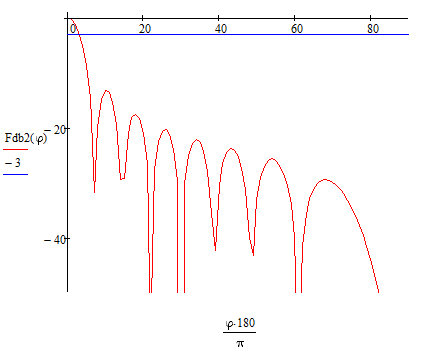
Рисунок 5 - Диаграмма направленности антенны по мощности электрического поля в вертикальной плоскости

Пункт 4.

В горизонтальной плоскости:

Половинный угол 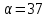градусов. Ширина главного лепестка ДН равна 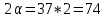градуса.

В вертикальной плоскости:

Половинный угол 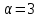градуса. Ширина главного лепестка ДН равна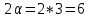
градусов.

Уровень первого бокового лепестка равен -13,52 дБ.

Задание №2. Входное сопротивление симметричного вибратора. Характеристики, определяющие степень согласования антенн.

Пункт 1.

В случае симметричного вибратора входное сопротивление 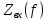определяется конструктивными параметрами и рассчитывается следующим образом: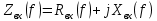



где 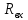и 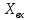– активная и реактивная составляющие комплексного входного сопротивления.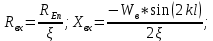



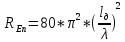– сопротивление излучения симметричного вибратора, Ом;

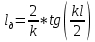– действующая длина симметричного вибратора, м;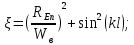



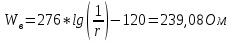– волновое сопротивление симметричного вибратора;

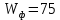Ом – волновое сопротивление фидера;

Проведём расчёт и построим графики зависимости активной и реактивной составляющих входного сопротивления.

Таблица 1 – Результаты расчёта

f, МГц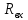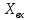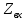






720
56.377
-35.688
56.38-35.69i

736
59.11
-28.261
59.11-28.26i

752
62.026
-20.976
62.03-20.98i

768
65.133
-13.833
65.13-13.83i

784
68.437
-6.838
68.44-6.84i

800
71.945
-0
71.94

816
75.658
6.666
75.66+6.67i

832
79.576
13.142
79.58+13.14i

848
83.694
19.403
83.69+19.4i

864
88
25.417
88+25.42i

880
92.476
31.149
92.48+31.15i



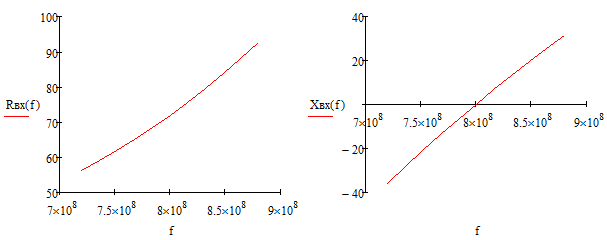
Рисунок 6 - Графики зависимости активной и реактивной составляющих входного сопротивления от частоты

Модуль комплексного коэффициента отражения от частоты рассчитывается по формуле:



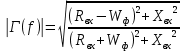
Таблица 2 – Результаты расчёта

f, МГц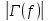


720
0.296

736
0.237

752
0.178

768
0.121

784
0.066

800
0.021

816
0.044

832
0.09

848
0.133

864
0.173

880
0.21



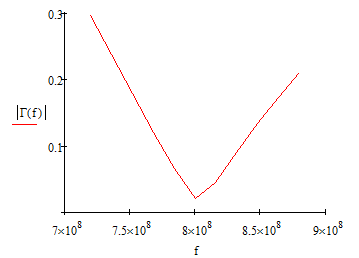
Рисунок 7 - График зависимости коэффициента отражения от частоты

Коэффициент стоячей волны по напряжению связан с модулем коэффициента отражения следующей зависимостью:



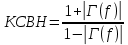
Таблица 3 – Результаты расчёта

f, МГц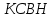


720
1.84

736
1.62

752
1.433

768
1.274

784
1.141

800
1.042

816
1.093

832
1.197

848
1.307

864
1.419

880
1.531



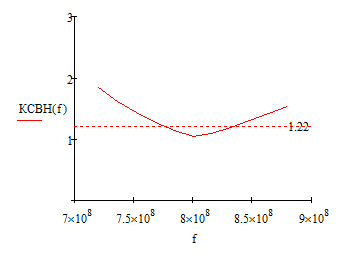
Рисунок 8 - График зависимости КСВН от частоты


Коэффициент бегущей волны определяется по формуле:



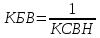
Таблица 4 – Результаты расчёта

f, МГц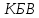


720
0.544

736
0.617

752
0.698

768
0.785

784
0.876

800
0.959

816
0.915

832
0.835

848
0.765

864
0.705

880
0.653



Рисунок 9 - График зависимости КБВ от частоты

Пункт 2.

Полоса пропускания по уровню КСВН=1,22: 775,9 – 834,2 МГц.

Ширина полосы пропускания: 834,2 – 775,9 = 58,3 МГц.

Задание №3. Формула идеальной радиопередачи.

Исходные данные:

Номер варианта: 5

Центральная частота диапазона = 5,3 ГГц

Расстояние между пунктами А и В = 25 км

Диаметр параболической антенны в пункте А = 2 м

Диаметр параболической антенны в пункте В = 1,5 м

Коэффициент использования апертуры антенны = 0,55

Мощность передатчика = 30 дБм
Пункт 1.

Волны дециметрового и сантиметрового диапазона не обладают свойством огибать сферическую поверхность Земли, поэтому необходимо обязательно рассчитать условный нулевой уровень профиля пролёта Z(x).



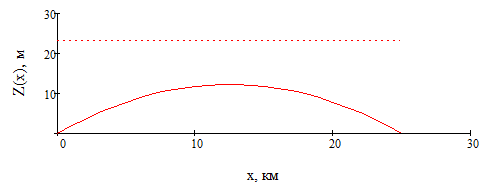
Рисунок 10 – Условный нулевой уровень профиля пролёта



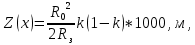
где 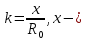текущая координата, км

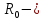протяжённость пролёта, км

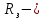радиус Земли, равный 6370 км.

Смотрите также файлы