ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 41
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа (Ряды)
k = 7
№1
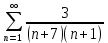
Методом неопределенных коэффициентов разложим на простейшие дроби:
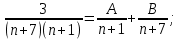
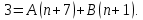
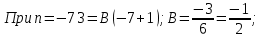
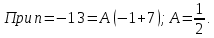
Имеем:
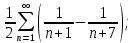
Вычислим частичную сумму:
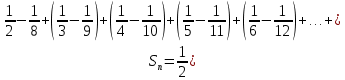
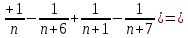
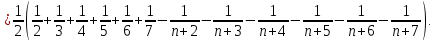
Перейдя к пределу:
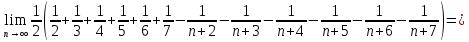
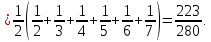
Ответ:
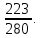
№2
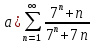
Проверим необходимое условие сходимости:
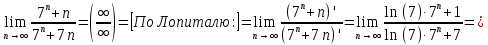
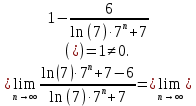
Не выполнен необходимый признак. Ряд расходится.
Ответ: расходится.
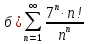
Исследуем по признаку Даламбера:
Используем признак Даламбера.
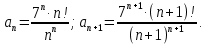
Перейдем к пределу:
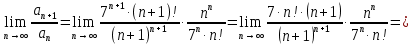
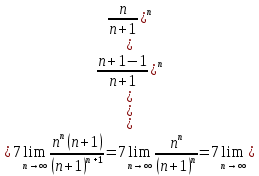
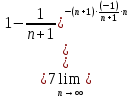
Следовательно, ряд расходится.
Ответ: расходится.
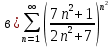
Исследуем по радикальному признаку Коши.
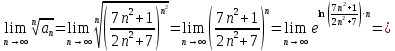
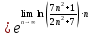
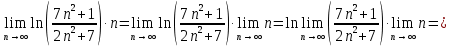
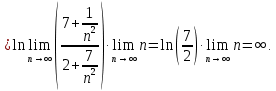
Ряд расходится.
Ответ: расходится.
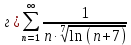
Применим признак сравнения и рассмотрим функцию:
Рассмотрим функцию:

функция на промежутке [1; +), следовательно, можно применить интегральный признак Коши.
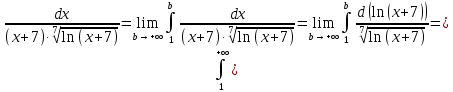
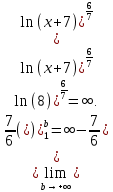
Так как несобственный интеграл второго рода расходится, то исходный ряд расходится.
По предельному признаку сравнения:
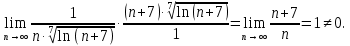
Следовательно, оба ряда расходятся.
Ответ: расходится.
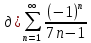
Используем признак Лейбница.
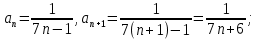
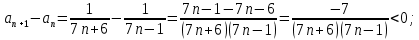
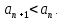
Первое условие выполняется.
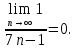
По признаку Лейбница ряд сходится.
Исследуем ряд на абсолютную сходимость.
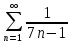
Сравним с гармоническим расходящимся рядом:
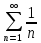
По предельному признаку сравнения:
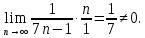
Следовательно, оба ряда расходятся.
Тогда ряд сходится условно.
Ответ: сходится условно.
№3
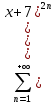
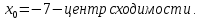
Найдем область сходимости.
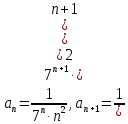
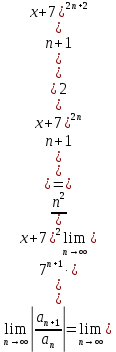
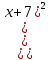
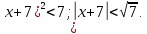
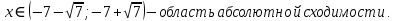
Исследуем поведение ряда на концах интервала сходимости.
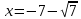
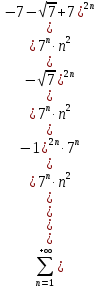
p = 2 > 1, ряд сходится.
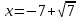

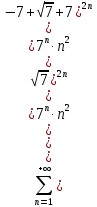
p = 2 > 1, ряд сходится.
Ответ: