Файл: Решение. Для достижения цели пауку нужно сделать 5 шагов вверх и 6 шагов вправо, т е. в общей сложности 11 шагов. Искомое число способов добраться до мухи равно числу различных способов выбрать 5 шагов вверх из возможных 11, т е..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Целеустремленный паук хочет доползти до мухи, попавшей в его паутину (см. рис.). При этом ползти он может только вверх и вправо по нитям паутины. Сколько есть различных способов у паука достигнуть свою цель?
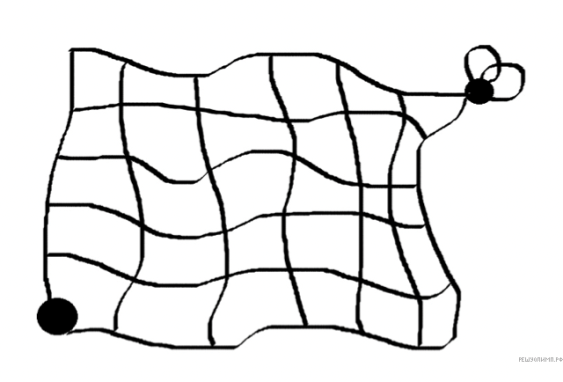
Решение. Для достижения цели пауку нужно сделать 5 шагов вверх и 6 шагов вправо, т. е. в общей сложности 11 шагов. Искомое число способов добраться до мухи равно числу различных способов выбрать 5 шагов вверх из возможных 11, т. е. всего
2) Целеустремленный паук хочет доползти до мухи, попавшей в его паутину (см. рисунок). При этом ползти он может только вверх и вправо по нитям паутины. Сколько есть различных способов у паука достигнуть свою цель?
Ответ: 126.
3) В коробке 9 синих, 4 красных и 12 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решение. Заметим, что возможны два случая, когда выбраны один синий и один красный фломастер: сначала выбрали синий, потом красный; сначала выбрали красный, потом синий. Эти события несовместны, следовательно, искомая вероятность равна P(С; К) + P(К; С):
Ответ: 0,12.
4) В клетке 6 белых и 4 серые мыши. Случайно выбирают 3-х мышей, не возвращая их обратно. Вычислить вероятность событий : а) все три мыши белые б) две белые и одна серая.
Всего — n = 6 + 4 = 10 шт.
а) Все три белые — И первая И вторая И третья — вероятность событий. «
И» равна произведению каждого из них. Вероятность события Р(3б) = 6/10 * 5/9 * 4/8 = 1/6
б) Две белых и серая — ИЛИ «ббс» ИЛИ «бсб» ИЛИ «сбб» — вероятность событий «ИЛИ» равна сумме вероятностей каждого из них. Вероятность Р(2бс) = (6/10*5/9*4/8) + (6/10*4/9*5/8) + (4/10*6/9*5/8) = 3 * (6*5*4)/(10*9*8) = 3 * 120/720 = 3 * 1/6 = 1/2
5) Технический контроль из партии в 10 изделий проверяет взятые наудачу 3 изделия. Партия не принимается, если среди трех проверяемых изделий окажется хотя бы одно бракованное. Определить вероятность приемки партии, если в ней окажется 5 бракованных изделий.
Решение. Обозначим через А событие, состоящее в том, что партия изделий будет принята. Общее число исходов, состоящее в проверке трех наудачу взятых изделий из 10, равно
6) На полке 6 книг по математике и 4 по физике. Найти вероятность того, что среди выбранных наудачу пяти книг будут три по математике и две по физике.
Решение. Три книги по математике можно выбрать
7) В квадрате АВСД случайным образом выбирается точка Х. Найдите вероятность того, что эта точка принадлежит трапеции АМСД, где точка М : а) середина стороны ВС; б) делит отрезок СB в отношении 1:2, считая от точки B.
Решение а):
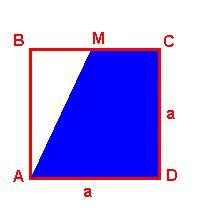
P = SAMCD / SABCD
S AMCD = (a+0,5a)*a/2 = 1,5a2 / 2 = 0,75a2
S ABCD = a2
P = 0,75 a2 / a2 = 0,75
Решение б):
Р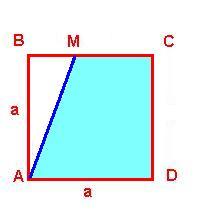 BM : MC = 1: 2; MC = 2/3 a.
BM : MC = 1: 2; MC = 2/3 a.
S AMCD = (a+ 2/3 a) * a /2 = 5/3 a2 /2 = 5/6 a2
P = (5/6)a2 / a2 = 5/6 ≈ 0,83
8) В круге случайным образом выбирается точка. Найдите вероятность того что эта точка принадлежит вписанному в круг квадрату;
Решение: Пусть сторона квадрата равна а, тогда его диагональ d=а√2 является диаметром описанной окружности, ее радиус равен R= d/2 = a√2 /2.
P = Sквадр. / Sкруга = а2 / (пR2) = a2 / (п*2a2 /4) = 2/п = 2 / 3,14 ≈ 0,64 .
9) В круге случайным образом выбирается точка. Найдите вероятность того что эта точка принадлежит вписанному в круг равностороннему треугольнику.
Решение. Пусть сторона равностороннего 3-ка равна а. Тогда его площадь равна SΔ= a2√3/4.
Радиус описанной окружности равен Rоп= а/√3. Sкруга = п*Rоп2 = па2 /3.
Вероятность попадания точки в треугольник равна
Р = SΔ / Sкруга= (а2√3/4) / (пa2/3) = 3√3 /(4п) ≈ 0,41
10) В таблице показано распределение случайной величины X. Найдите
| Значения X | −1 | 2 | 4 | 6 |
| Вероятности | 0,6 | 0,1 | 0,2 | 0,1 |
Решение. Математическое ожидание E случайной дискретной величины X, которая может принимать четыре возможных значения, равно
По условию:
Тогда
Ответ: 1.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0.5 | 0.3 | x | 0.03 | 0.02 |
Дано распределение случайной величины X. Найдите математическое ожидание E X.
х = 1 – (0,5+0,3+0,03+0,02) = 1 – 0,85 = 0,15
M[x] = 0*0.5 + 1*0.3 + 2*0.15 + 3*0.03 + 4*0.02 = 0.77
| | | | | | | |
| | | | | |