Файл: Исследование зависимости критической частоты вращения вала от величины массы насаженной детали и жесткости вала Тема Валы и оси Задание.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 91

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическое задание 3

Исследование зависимости критической частоты вращения вала от величины массы насаженной детали и жесткости валаТема 5. Валы и осиЗаданиеОпределите расчетное значение критической частоты вращения вала. Исследуйте влияние на величину критической частоты вращения жесткости вала, массы насаженной детали. По результатам расчетов сделайте и запишите выводы, ответив на следующие вопросы:

  1. Какие параметры влияют на критическую частоту вращения?

  2. Как изменится критическая частота вращения при изменении массы насаженной детали?

  3. Как изменится критическая частота вращения при увеличении (уменьшении) жесткости вала?
Номер варианта определяется согласно табл. 3.1 по первым буквам фамилии.Рис. 3.1. Вращающийся валСхема вращающегося вала (рис. 3.1) состоит из вала 1 диаметром d с насаженным на него диском 2 массой mд. Для увеличения массы диска на него могут навинчиваться два дополнительных груза 3, каждый массой mг.Вал 1 вращается в двух сферических подшипниках, которые устанавливаются в опорах 4 (передняя опора) и 5 (задняя опора). Передняя опора неподвижна. Задняя опора выполнена в виде пиноли, которая выдвигается с помощью винта с маховиком 6 и рукояткой. Таким образом, длина вала может изменяться от L до L1. Таблица 3.1 Выбор варианта задания

Первая буква фамилии
Вариант
Диаметр вала, мм
Масса диска mд, кг
Масса груза mг, кг
Длина вала L, мм
Длина вала L1, мм

А, М, Ч
1
8
1.5
0,4
500
550

Б, Н, Ш
2
9
1,7
0,4
400
450

В, О, Щ
3
10
1,8
0,5
420
470

Г, П, Э
4
11
1,9
0,6
450
500

Д, Р, Ю
5
12
2,0
0,7
600
650

Е, С, Я
6
13
2,1
0,8
650
700

Ж, Т
7
14
2,2
0,8
430
480

З, У
8
15
2,3
0,9
620
670

И, Ф
9
16
2,4
0,9
680
730

К, Х
10
17
2,5
0,9
700
750

Л, Ц
0
18
2,6
0,9
720
770
Рекомендации к выполнению задания 31. Выполнить необходимые расчеты согласно методическим указаниям.2. Оформить решение задачи с пояснениями хода решения, записать выводы.Методические указанияВалы – это детали, предназначенные для передачи крутящего момента вдоль своей оси и для поддержания вращающихся деталей машин. Основное практическое значение для валов имеют расчеты валов на колебания для предотвращения резонанса колебаний, заключающиеся в определении критической частоты вращения.Резонансом называется явление резкого нарастания амплитуд колебаний при совпадении или кратности частот вынужденных и свободных колебаний системы.Вынужденные колебания системы с одной степенью свободы описываются уравнением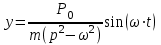, (3.1)где у – амплитуда вынужденных колебаний массы m;m – масса вращающегося вала;Р0–амплитуда возмущающей силы 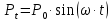; 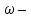частота вынужденных колебаний системы;р – частота свободных колебаний системы.Уравнение (3.1) позволяет отметить, что 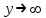при 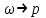, а при 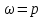наступает резонанс, при котором может произойти разрушение вала.Частоту вращения, при которой наступает резонанс, называют критической и определяют по формуле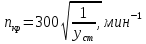, (3.2)где yст– наибольший статический прогиб вала, см.Если рассмотреть вращающийся вал массой тв, на который насажена деталь в виде диска массой mД, то максимальный статический прогиб вала под диском определяется по формуле 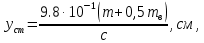(3.3)где с – жесткость вращающейся системы, Н/мм;т – масса насаженной детали, кг;
тв–масса вала, определяемая по формуле 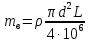, кг, (3.4)где ρ – плотность материала вала, для стали ρ = 7800 кг/м3;d – диаметр вала, см;L – расстояние между опорами, см.Если нагрузить вал с насаженной деталью усилием статического прогиба в 100 Н, то жесткость: 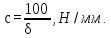(3.5)Жесткие валы работают в дорезонансной зоне, причем для уменьшения опасности резонанса повышают их жесткость и, следовательно, собственные частоты колебаний. При больших частотах вращения, например, в быстроходных турбинах и центрифугах, применяют валы повышенной податливости (гибкие), работающие в зарезонансной зоне. Проход через критические частоты вращения во избежание аварий осуществляют с возможно большей скоростью.Порядок расчета

  1. Определите массу вала по формуле 3.4, если расстояние между опорами равно L.

  2. Рассчитайте жесткость вращающей системы по формуле (3.5), величину статического прогиба по формуле (3.3) – величина δ задана в табл. 3.2 – и критическую частоту вращения по формуле (3.2).

  3. Добавьте к диску 2 дополнительные грузы 3, увеличив массу насаженной детали.

  4. Рассчитайте жесткость вращающей системы по формуле (3.5), величину статического прогиба по формуле (3.3) и критическую частоту вращения по формуле (3.2).

  5. Увеличьте длину вала до значения L1, открепите дополнительные грузы. Определите массу вала по формуле 3.4.

  6. Рассчитайте жесткость вращающей системы по формуле (3.5), величину статического прогиба по формуле (3.3) и критическую частоту вращения по формуле (3.2).

  7. Добавьте к диску 2 дополнительные грузы 3, увеличив массу насаженной детали.

  8. Рассчитайте жесткость вращающей системы по формуле (3.5), величину статического прогиба по формуле (3.3) и критическую частоту вращения по формуле (3.2).

  9. Результаты расчетов занесите в табл. 3.2.
Таблица 3.2Результаты вычислений

№

L,

см
,

кг
mД, кг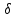
,

мм
, Н/мм
,

см
,

мин–1

1









0,6









2









0,7









3









0,65









4









0,8

































  1. Сделайте выводы.

Смотрите также файлы