x	lny	x2	lny2	x*lny
	10	1,9988	100	3,9951	19,9877
	20	2,8987	400	8,4023	57,9734
	30	3,7986	900	14,4296	113,9589
	40	4,6986	1600	22,0766	187,9428
	50	5,5986	2500	31,3448	279,9322
∑	150	18,9933	5500	80,2484	659,795

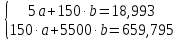Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.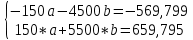
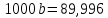Откуда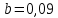
Найдём :
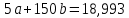
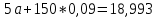
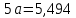
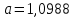Уравнение экспоненциальной зависимости: y = e^1,099e^0,09x = 3,00046e^0,09x
Степенная зависимость

Для расчёта параметров регрессии построим расчётную таблицу (табл. 1)

	lnx	lny	lnx2	lny2	lnx*lny
	2,3026	1,9988	5,3019	3,9951	4,6023
	2,9957	2,8987	8,9744	8,4023	8,6836
	3,4012	3,7986	11,5681	14,4296	12,9199
	3,6889	4,6986	13,6078	22,0766	17,3325
	3,912	5,5986	15,3039	31,3448	21,902
∑	16,3004	18,9933	54,7562	80,2484	65,4404

---

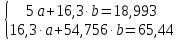Домножим 1-е уравнение системы на (-3,26), получим систему, которую решим методом алгебраического сложения,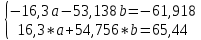
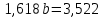Откуда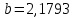
Найдём :
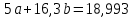
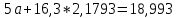
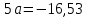
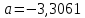Уравнение степенной зависимости: y = e^-3,3060x^2,1793 = 0,03666x^2,1793
Логарифмическая зависимость

Для расчёта параметров регрессии построим расчётную таблицу (табл, 1)

	lnx	y	lnx2	y2	ln(x)*y
	2,3026	7,38	5,3019	54,4644	16,9931
	2,9957	18,15	8,9744	329,4225	54,3725
	3,4012	44,64	11,5681	1992,7296	151,8295
	3,6889	109,79	13,6078	12053,8441	405,0021
	3,912	270,06	15,3039	72932,4036	1056,4809
∑	16,3004	450,02	54,7562	87362,8642	1684,6781

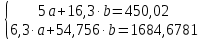Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.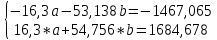


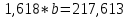Откуда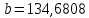

---

Найдем :
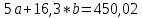
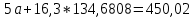
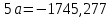
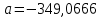Уравнение логарифмической зависимости: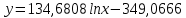
Показательная зависимость

	x	lny	x2	lny2	x*lny
	10	1,9988	100	3,9951	19,9877
	20	2,8987	400	8,4023	57,9734
	30	3,7986	900	14,4296	113,9589
	40	4,6986	1600	22,0766	187,9428
	50	5,5986	2500	31,3448	279,9322
∑	150	18,9933	5500	80,2484	659,795

Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.
Откуда
Найдем :
Уравнение показательной зависимости: y = e^1,0988*e^0,09x = 3,00046*1,09417^x

1. 
   Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
   

---

Таблица 4. Корреляционный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

Решение:
Для расчёта параметров регрессии построим расчётную таблицу

	x	y	x2	y2	x*y
	10	7,38	100	54,4644	73,8
	20	18,15	400	329,4225	363
	30	44,64	900	1992,7296	1339,2
	40	109,79	1600	12053,8441	4391,6
	50	270,06	2500	72932,4036	13503
∑	150	450,02	5500	87362,8642	19670,6

Выборочные средние:





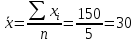
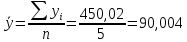
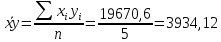Выборочные дисперсии: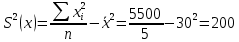

---

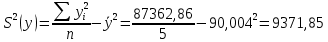
Среднеквадратическое отклонение:





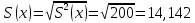
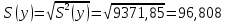
Рассчитываем количественное значение коэффициента парной линейной корреляции по формуле:



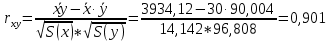
По шкале Чеддока модуль коэффициента парной линейной корреляции расположен в числовом интервале 0,9 – 1, значит, связь между х и у весьма высокая и прямая.

---

Смотрите также файлы

• Принципы расчета нормативов допустимых выбросов (ндв), структура документа и система утверждения.ppt

• Характеристика коллектива 7 класса.docx

• Конспект утренней гимнастики с обручем в средней группе.docx

• Для решения этой задачи мы используем теоретический материал, изложенный в работах разных авторов, например, Н. Н. Барановой, м в. Григорьевой, Леонида Пономареко и др.docx

• Тесты по курсу Агроэкономика с основами организации.doc