Файл: Лабораторная работа 1 Изгиб консольной балки и 2 и 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«Определение модуля Юнга при растяжении»
Абсолютная деформация: ∆L=P*L0/(E*S0)
Модуль Юнга: E=P*L0/(∆L*S0)
Относительное удлинение: ε=∆L/L , ∆L=ε *L
Напряжение: δ=P/S
δ/ ε=tgα
δ / ε=E, E= tgα – Модуль Юнга первого рода
/ ε=E, E= tgα – Модуль Юнга первого рода










 a d0 c
a d0 c



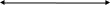
 d0 L0
d0 L0
Материалы, представленные в отчете:
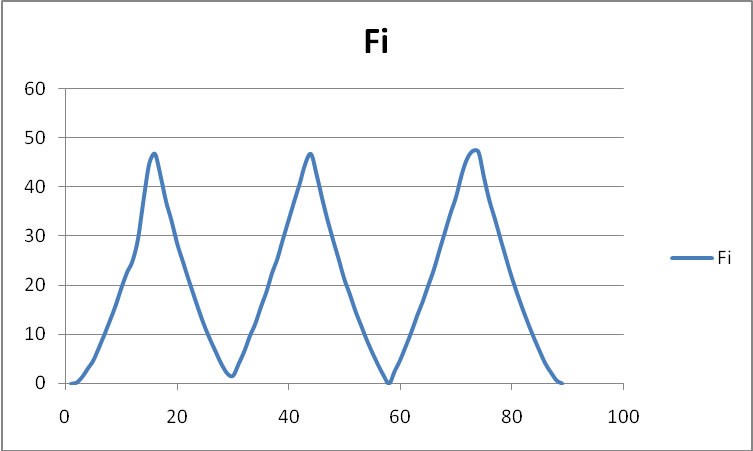
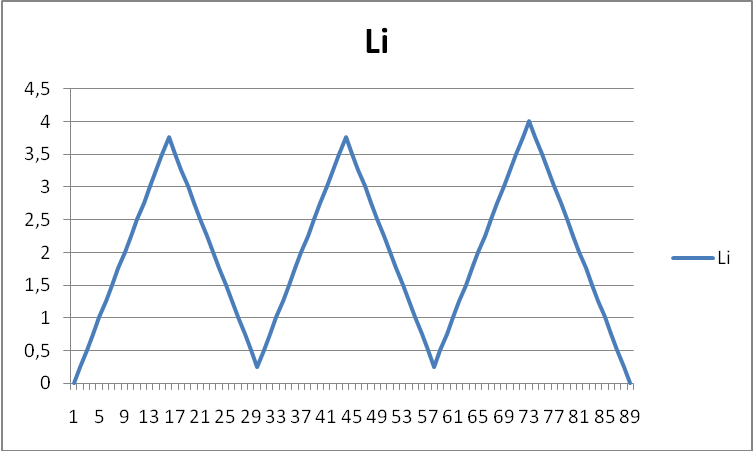
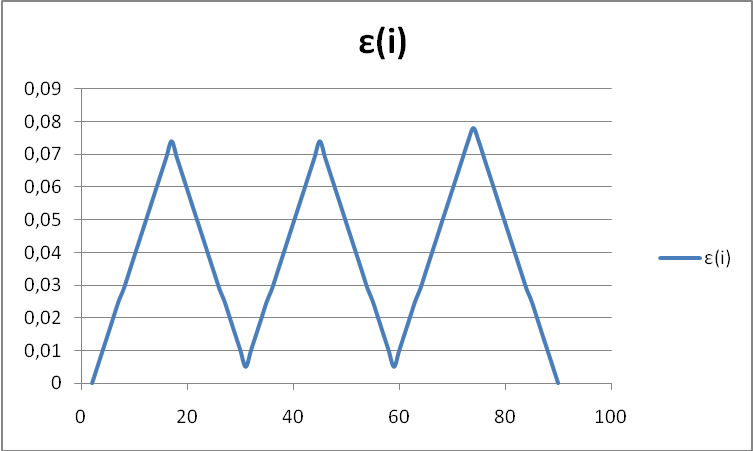
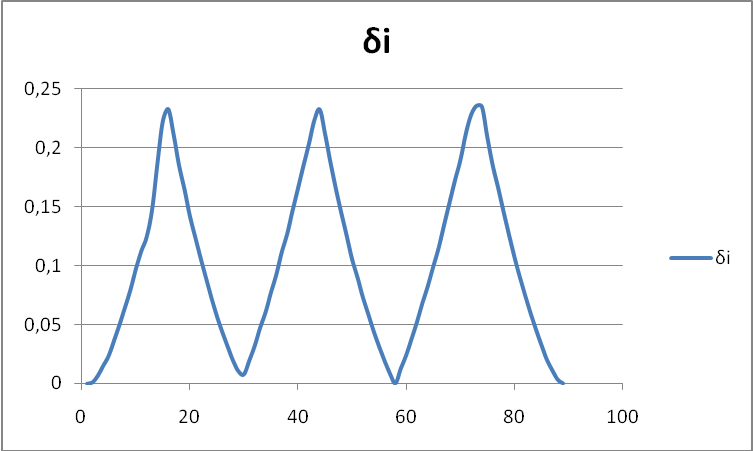
По результатам лаб. Работы представить отчет, в котором привести эскиз образца, графики измерения Pi, ∆Li, δi, εi, результаты расчетов и выводы. В выводах дать объяснение смысла модуля Юнга и указать величины, влияющие на величину модуля упругости первого рода.
Физический смысл модуля Юнга: он равен напряжению, соответствующему увеличению длины стержня вдвое, если бы при такой нагрузке тело оставалось упругим и подчинялось бы закону Гука. Действительно,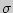 численно равно
численно равно 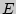 при
при 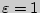 , т.е. при
, т.е. при 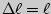 .
.
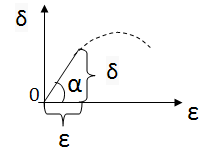
Геометрический смысл модуля Юнга: модуль нормальной упругости соответствует тангенсу угла α наклона начального участка диаграммы растяжения.
Факторы, влияющие на величину модуля Юнга 1-го рода
E= δ/ ε
1)Площадь поперечного сечения образца
2) Материал образца
3)Длина образца
Лабораторная работа № 4
«Испытание материалов на сжатие»
δпусж=Fпу/S0 δреж=Fреж/S0 δ25=F25/S0
ε%=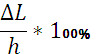 1
1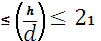
Абсолютная деформация: ∆L=P*L0/(E*S0)
Модуль Юнга: E=P*L0/(∆L*S0)
Относительное удлинение: ε=∆L/L , ∆L=ε *L
Напряжение: δ=P/S
δ/ ε=tgα
δ
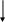 / ε=E, E= tgα – Модуль Юнга первого рода
/ ε=E, E= tgα – Модуль Юнга первого рода









 a d0 c
a d0 c


 d0 L0
d0 L0Материалы, представленные в отчете:
По результатам лаб. Работы представить отчет, в котором привести эскиз образца, графики измерения Pi, ∆Li, δi, εi, результаты расчетов и выводы. В выводах дать объяснение смысла модуля Юнга и указать величины, влияющие на величину модуля упругости первого рода.
| № п.п. | dio, мм | do, мм | Lio, мм | Lo, мм | ∆Li, мм | ε(i) | Fi (H) | МПа | ||
| δi | Ei | E | ||||||||
| 1 | 16 | 16 | 51 | 51 | 0 | 0 | 0,01 | 0 | 0 | 0 |
| 2 | 16 | 16 | 51 | 51 | 0,25 | 0,005 | 0,25 | 0,001 | 0,25 | 0,25 |
| 3 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 1,4 | 0,007 | 0,70 | 0,95 |
| 4 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 3,1 | 0,015 | 1,03 | 1,97 |
| 5 | 16 | 16 | 51 | 51 | 1 | 0,02 | 4,8 | 0,024 | 1,19 | 3,17 |
| 6 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 7,4 | 0,037 | 1,47 | 4,64 |
| 7 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 10,1 | 0,050 | 1,73 | 6,37 |
| 8 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 13 | 0,065 | 1,90 | 8,28 |
| 9 | 16 | 16 | 51 | 51 | 2 | 0,039 | 16 | 0,080 | 2,04 | 10,32 |
| 10 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 19,5 | 0,097 | 2,21 | 12,52 |
| 11 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 22,6 | 0,112 | 2,30 | 14,82 |
| 12 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 25 | 0,124 | 2,30 | 17,12 |
| 13 | 16 | 16 | 51 | 51 | 3 | 0,059 | 29,6 | 0,147 | 2,50 | 19,62 |
| 14 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 37,6 | 0,187 | 2,92 | 22,54 |
| 15 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 44,8 | 0,223 | 3,23 | 25,77 |
| 16 | 16 | 16 | 51 | 51 | 3,75 | 0,074 | 46,85 | 0,233 | 3,15 | 28,92 |
| 17 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 42,5 | 0,211 | 3,06 | 31,99 |
| 18 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 37,2 | 0,185 | 2,89 | 34,88 |
| 19 | 16 | 16 | 51 | 51 | 3 | 0,059 | 33,2 | 0,165 | 2,80 | 37,68 |
| 20 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 28,6 | 0,142 | 2,64 | 40,32 |
| 21 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 25 | 0,124 | 2,54 | 42,86 |
| 22 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 21,4 | 0,106 | 2,42 | 45,28 |
| 23 | 16 | 16 | 51 | 51 | 2 | 0,039 | 18 | 0,090 | 2,30 | 47,57 |
| 24 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 14,6 | 0,073 | 2,14 | 49,71 |
| 25 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 11,5 | 0,057 | 1,97 | 51,68 |
| 26 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 8,8 | 0,044 | 1,75 | 53,43 |
| 27 | 16 | 16 | 51 | 51 | 1 | 0,02 | 6,3 | 0,031 | 1,57 | 55,00 |
| 28 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 3,9 | 0,019 | 1,29 | 56,30 |
| 29 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 2,1 | 0,010 | 1,04 | 57,34 |
| 30 | 16 | 16 | 51 | 51 | 0,25 | 0,005 | 1,61 | 0,008 | 1,60 | 58,94 |
| 31 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 4 | 0,020 | 1,99 | 60,93 |
| 32 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 6,5 | 0,032 | 2,16 | 63,09 |
| 33 | 16 | 16 | 51 | 51 | 1 | 0,02 | 9,6 | 0,048 | 2,39 | 65,48 |
| 34 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 12,2 | 0,061 | 2,43 | 67,91 |
| 35 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 15,6 | 0,078 | 2,68 | 70,58 |
| 36 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 18,7 | 0,093 | 2,74 | 73,32 |
| 37 | 16 | 16 | 51 | 51 | 2 | 0,039 | 22,5 | 0,112 | 2,87 | 76,19 |
| 38 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 25,6 | 0,127 | 2,90 | 79,09 |
| 39 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 29,6 | 0,147 | 3,01 | 82,09 |
| 40 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 33,4 | 0,166 | 3,08 | 85,17 |
| 41 | 16 | 16 | 51 | 51 | 3 | 0,059 | 37,2 | 0,185 | 3,14 | 88,31 |
| 42 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 40,9 | 0,204 | 3,18 | 91,49 |
| 43 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 44,9 | 0,223 | 3,24 | 94,73 |
| 44 | 16 | 16 | 51 | 51 | 3,75 | 0,074 | 46,78 | 0,233 | 3,15 | 97,87 |
| 45 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 42,6 | 0,212 | 3,07 | 100,94 |
| 46 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 37,7 | 0,188 | 2,93 | 103,87 |
| 47 | 16 | 16 | 51 | 51 | 3 | 0,059 | 33,2 | 0,165 | 2,80 | 106,67 |
| 48 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 29,1 | 0,145 | 2,68 | 109,36 |
| 49 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 25,2 | 0,125 | 2,56 | 111,92 |
| 50 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 21,2 | 0,105 | 2,40 | 114,31 |
| 51 | 16 | 16 | 51 | 51 | 2 | 0,039 | 18,1 | 0,090 | 2,31 | 116,62 |
| 52 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 14,7 | 0,073 | 2,15 | 118,77 |
| 53 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 11,8 | 0,059 | 2,02 | 120,80 |
| 54 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 8,9 | 0,044 | 1,77 | 122,57 |
| 55 | 16 | 16 | 51 | 51 | 1 | 0,02 | 6,3 | 0,031 | 1,57 | 124,14 |
| 56 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 3,9 | 0,019 | 1,29 | 125,43 |
| 57 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 1,7 | 0,008 | 0,85 | 126,28 |
| 58 | 16 | 16 | 51 | 51 | 0,25 | 0,005 | 0,081 | 0,000 | 0,08 | 126,36 |
| 59 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 2,6 | 0,013 | 1,29 | 127,65 |
| 60 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 4,9 | 0,024 | 1,63 | 129,28 |
| 61 | 16 | 16 | 51 | 51 | 1 | 0,02 | 7,7 | 0,038 | 1,92 | 131,19 |
| 62 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 10,6 | 0,053 | 2,11 | 133,30 |
| 63 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 13,8 | 0,069 | 2,37 | 135,67 |
| 64 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 16,7 | 0,083 | 2,44 | 138,11 |
| 65 | 16 | 16 | 51 | 51 | 2 | 0,039 | 20 | 0,100 | 2,55 | 140,67 |
| 66 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 23,2 | 0,115 | 2,62 | 143,29 |
| 67 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 27,1 | 0,135 | 2,75 | 146,04 |
| 68 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 30,9 | 0,154 | 2,85 | 148,89 |
| 69 | 16 | 16 | 51 | 51 | 3 | 0,059 | 34,7 | 0,173 | 2,93 | 151,82 |
| 70 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 38,1 | 0,190 | 2,96 | 154,78 |
| 71 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 42,6 | 0,212 | 3,07 | 157,85 |
| 72 | 16 | 16 | 51 | 51 | 3,75 | 0,074 | 45,9 | 0,228 | 3,09 | 160,94 |
| 73 | 16 | 16 | 51 | 51 | 4 | 0,078 | 47,42 | 0,236 | 3,03 | 163,96 |
| 74 | 16 | 16 | 51 | 51 | 3,75 | 0,074 | 47,26 | 0,235 | 3,18 | 167,14 |
| 75 | 16 | 16 | 51 | 51 | 3,5 | 0,069 | 42 | 0,209 | 3,03 | 170,17 |
| 76 | 16 | 16 | 51 | 51 | 3,25 | 0,064 | 37,2 | 0,185 | 2,89 | 173,06 |
| 77 | 16 | 16 | 51 | 51 | 3 | 0,059 | 33,4 | 0,166 | 2,82 | 175,88 |
| 78 | 16 | 16 | 51 | 51 | 2,75 | 0,054 | 29,34 | 0,146 | 2,70 | 178,58 |
| 79 | 16 | 16 | 51 | 51 | 2,5 | 0,049 | 25,4 | 0,126 | 2,58 | 181,16 |
| 80 | 16 | 16 | 51 | 51 | 2,25 | 0,044 | 21,6 | 0,107 | 2,44 | 183,61 |
| 81 | 16 | 16 | 51 | 51 | 2 | 0,039 | 18,2 | 0,091 | 2,32 | 185,93 |
| 82 | 16 | 16 | 51 | 51 | 1,75 | 0,034 | 15 | 0,075 | 2,20 | 188,12 |
| 83 | 16 | 16 | 51 | 51 | 1,5 | 0,029 | 12 | 0,060 | 2,06 | 190,18 |
| 84 | 16 | 16 | 51 | 51 | 1,25 | 0,025 | 9,2 | 0,046 | 1,83 | 192,01 |
| 85 | 16 | 16 | 51 | 51 | 1 | 0,02 | 6,6 | 0,033 | 1,64 | 193,66 |
| 86 | 16 | 16 | 51 | 51 | 0,75 | 0,015 | 4,1 | 0,020 | 1,36 | 195,02 |
| 87 | 16 | 16 | 51 | 51 | 0,5 | 0,01 | 2,3 | 0,011 | 1,14 | 196,16 |
| 88 | 16 | 16 | 51 | 51 | 0,25 | 0,005 | 0,7 | 0,003 | 0,70 | 196,86 |
| 89 | 16 | 16 | 51 | 51 | 0 | 0 | 0,06 | 0,000 | 0,00 | 196,86 |
Физический смысл модуля Юнга: он равен напряжению, соответствующему увеличению длины стержня вдвое, если бы при такой нагрузке тело оставалось упругим и подчинялось бы закону Гука. Действительно,
Геометрический смысл модуля Юнга: модуль нормальной упругости соответствует тангенсу угла α наклона начального участка диаграммы растяжения.

Факторы, влияющие на величину модуля Юнга 1-го рода
E= δ/ ε
1)Площадь поперечного сечения образца
2) Материал образца
3)Длина образца




Лабораторная работа № 4
«Испытание материалов на сжатие»
δпусж=Fпу/S0 δреж=Fреж/S0 δ25=F25/S0
ε%=
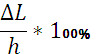 1
1| Геометрические параметры исследуемых образцов | |||||
| № образца | № Измерения | Линейные размеры образцов (мм) | |||
| ai (di) | hi | a0 | h0 | ||
| 1(латунь) | 1 | 8 | 13 | 8 | 13 |
| 2(алюминий) | 1 | 8 | 13 | 8 | 13 |
| 3(медь) | 1 | 8 | 12,26 | 8 | 12,63 |
| 3(медь) | 2 | 8 | 13 | 8 | 12,63 |
| 4(нерж.) | 1 | 8 | 10 | 8 | 10 |
| Геометрические параметры исследуемых образцов после испытаний | ||||
| № образца | № Измерения | Линейные размеры образцов (мм) | ||
| a1(d11/d12) | A2(d21/d22) | h1/h2 | ||
| 1(латунь) | 1 | 9 | 9 | 9,5 |
| 2(алюминий) | 1 | 19 | 15,5 | 3 |
| 3(медь) | 1 | 14 | 11,5 | 5 |
| 4(нерж.) | 1 | 9 | 9 | 7 |
| Результаты испытаний материалов на сжатие | ||||||||
| № п.п. | № измерения | Fi (H) | δi (H) | ε(i) | ||||
| 1 | 1 | 0,08 | 0,0016 | 0,0000 | ||||
| 1 | 2 | 0,08 | 0,0016 | 0,3846 | ||||
| 1 | 3 | 2,1 | 0,0418 | 1,9231 | ||||
| 1 | 4 | 3,6 | 0,0717 | 3,8462 | ||||
| 1 | 5 | 5,7 | 0,1135 | 5,7692 | ||||
| 1 | 6 | 7,8 | 0,1553 | 7,6923 | ||||
| 1 | 7 | 10,3 | 0,2050 | 9,6154 | ||||
| 1 | 8 | 12,2 | 0,2428 | 11,5385 | ||||
| 1 | 9 | 13,8 | 0,2747 | 13,4615 | ||||
| 1 | 10 | 14,8 | 0,2946 | 15,3846 | ||||
| 1 | 11 | 15,9 | 0,3165 | 17,3077 | ||||
| 1 | 12 | 17,1 | 0,3404 | 19,2308 | ||||
| 1 | 13 | 18,2 | 0,3623 | 21,1538 | ||||
| 1 | 14 | 19,1 | 0,3802 | 23,0769 | ||||
| 1 | 15 | 20 | 0,3981 | 25,0000 | ||||
| 1 | 16 | 21 | 0,4180 | 26,9231 | ||||
| 1 | 17 | 22,1 | 0,4399 | 28,8462 | ||||
| 1 | 18 | 23,2 | 0,4618 | 30,7692 | ||||
| 1 | 19 | 25,2 | 0,5016 | 32,6923 | ||||
| 1 | 20 | 26,4 | 0,5255 | 34,6154 | ||||
| 1 | 21 | 27,5 | 0,5474 | 36,5385 | ||||
| 1 | 22 | 28,6 | 0,5693 | 38,4615 | ||||
| 1 | 23 | 29,7 | 0,5912 | 40,3846 | ||||
| 1 | 24 | 30,8 | 0,6131 | 42,3077 | ||||
| 1 | 25 | 31,8 | 0,6330 | 44,2308 | ||||
| 1 | 26 | 32,8 | 0,6529 | 46,1538 | ||||
| 1 | 27 | 33,5 | 0,6668 | 48,0769 | ||||
| 1 | 28 | 33,6 | 0,6688 | 50,0000 | ||||
| 1 | 29 | 33,81 | 0,6730 | 51,9231 | ||||
| 2 | 30 | 0,4 | 0,0080 | 0 | ||||
| 2 | 31 | 1,5 | 0,0299 | 1,923077 | ||||
| 2 | 32 | 2,8 | 0,0557 | 3,846154 | ||||
| 2 | 33 | 4,3 | 0,0856 | 5,769231 | ||||
| 2 | 34 | 5,4 | 0,1075 | 7,692308 | ||||
| 2 | 35 | 5,9 | 0,1174 | 9,615385 | ||||
| 2 | 36 | 6 | 0,1194 | 11,53846 | ||||
| 2 | 37 | 6,1 | 0,1214 | 13,46154 | ||||
| 2 | 38 | 6,2 | 0,1234 | 15,38462 | ||||
| 2 | 39 | 6,3 | 0,1254 | 17,30769 | ||||
| 2 | 40 | 6,4 | 0,1274 | 19,23077 | ||||
| 2 | 41 | 6,5 | 0,1294 | 21,15385 | ||||
| 2 | 42 | 6,6 | 0,1314 | 23,07692 | ||||
| 2 | 43 | 6,7 | 0,1334 | 25 | ||||
| 2 | 44 | 6,8 | 0,1354 | 26,92308 | ||||
| 2 | 45 | 7 | 0,1393 | 28,84615 | ||||
| 2 | 46 | 7,2 | 0,1433 | 30,76923 | ||||
| 2 | 47 | 7,3 | 0,1453 | 32,69231 | ||||
| 2 | 48 | 7,4 | 0,1473 | 34,61538 | ||||
| 2 | 49 | 7,6 | 0,1513 | 36,53846 | ||||
| 2 | 50 | 7,7 | 0,1533 | 38,46154 | ||||
| 2 | 51 | 7,8 | 0,1553 | 40,38462 | ||||
| 2 | 52 | 8 | 0,1592 | 42,30769 | ||||
| 2 | 53 | 8,2 | 0,1632 | 44,23077 | ||||
| 2 | 54 | 8,5 | 0,1692 | 46,15385 | ||||
| 2 | 55 | 8,8 | 0,1752 | 48,07692 | ||||
| 2 | 56 | 9,1 | 0,1811 | 50 | ||||
| 2 | 57 | 9,4 | 0,1871 | 51,92308 | ||||
| 2 | 58 | 9,8 | 0,1951 | 53,84615 | ||||
| 2 | 59 | 10,2 | 0,2030 | 55,76923 | ||||
| 2 | 60 | 10,7 | 0,2130 | 57,69231 | ||||
| 2 | 61 | 11,3 | 0,2249 | 59,61538 | ||||
| 2 | 62 | 11,9 | 0,2369 | 61,53846 | ||||
| 2 | 63 | 12,6 | 0,2508 | 63,46154 | ||||
| 2 | 64 | 14,6 | 0,2906 | 65,38462 | ||||
| 2 | 65 | 14,8 | 0,2946 | 67,30769 | ||||
| 2 | 66 | 15,6 | 0,3105 | 69,23077 | ||||
| 2 | 67 | 16,4 | 0,3264 | 71,15385 | ||||
| 2 | 68 | 17,2 | 0,3424 | 73,07692 | ||||
| 2 | 69 | 18,1 | 0,3603 | 75 | ||||
| 2 | 70 | 19,1 | 0,3802 | 76,92308 | ||||
| 2 | 71 | 20 | 0,3981 | 78,84615 | ||||
| 2 | 72 | 21,3 | 0,4240 | 80,76923 | ||||
| 2 | 73 | 22,3 | 0,4439 | 82,69231 | ||||
| 2 | 74 | 23,6 | 0,4697 | 84,61538 | ||||
| 2 | 75 | 25,1 | 0,4996 | 86,53846 | ||||
| 2 | 76 | 26,6 | 0,5295 | 88,46154 | ||||
| 2 | 77 | 28,1 | 0,5593 | 90,38462 | ||||
| 2 | 78 | 29,7 | 0,5912 | 92,30769 | ||||
| 2 | 79 | 31,8 | 0,6330 | 94,23077 | ||||
| 2 | 80 | 33,3 | 0,6628 | 96,15385 | ||||
| 2 | 81 | 35,3 | 0,7026 | 98,07692 | ||||
| 2 | 82 | 37,7 | 0,7504 | 100 | ||||
| 2 | 83 | 39,9 | 0,7942 | 101,9231 | ||||
| 2 | 84 | 42,3 | 0,8420 | 103,8462 | ||||
| 2 | 85 | 44,7 | 0,8897 | 105,7692 | ||||
| 2 | 86 | 45,39 | 0,9035 | 107,6923 | ||||
| 3 | 87 | 0,22 | 0,0044 | 0 | ||||
| 3 | 88 | 1,4 | 0,0279 | 1,979414 | ||||
| 3 | 89 | 3,7 | 0,0736 | 3,958828 | ||||
| 3 | 90 | 5,5 | 0,1095 | 5,938242 | ||||
| 3 | 91 | 7,7 | 0,1533 | 7,917656 | ||||
| 3 | 92 | 10,1 | 0,2010 | 9,89707 | ||||
| 3 | 93 | 12,8 | 0,2548 | 11,87648 | ||||
| 3 | 94 | 15,7 | 0,3125 | 13,8559 | ||||
| 3 | 95 | 17,6 | 0,3503 | 15,83531 | ||||
| 3 | 96 | 18,4 | 0,3662 | 17,81473 | ||||
| 3 | 97 | 18,53 | 0,3688 | 19,79414 | ||||
| 3 | 98 | 18,48 | 0,3678 | 21,77356 | ||||
| 3 | 99 | 18,46 | 0,3674 | 23,75297 | ||||
| 3 | 100 | 18,48 | 0,3678 | 25,73238 | ||||
| 3 | 101 | 18,56 | 0,3694 | 27,7118 | ||||
| 3 | 102 | 18,68 | 0,3718 | 29,69121 | ||||
| 3 | 103 | 18,8 | 0,3742 | 31,67063 | ||||
| 3 | 104 | 19 | 0,3782 | 33,65004 | ||||
| 3 | 105 | 19,2 | 0,3822 | 35,62945 | ||||
| 3 | 106 | 19,4 | 0,3861 | 37,60887 | ||||
| 3 | 107 | 19,5 | 0,3881 | 39,58828 | ||||
| 3 | 108 | 19,7 | 0,3921 | 41,5677 | ||||
| 3 | 109 | 19,9 | 0,3961 | 43,54711 | ||||
| 3 | 110 | 20,1 | 0,4001 | 45,52652 | ||||
| 3 | 111 | 20,5 | 0,4080 | 47,50594 | ||||
| 3 | 112 | 20,9 | 0,4160 | 49,48535 | ||||
| 3 | 113 | 21,3 | 0,4240 | 51,46477 | ||||
| 3 | 114 | 21,8 | 0,4339 | 53,44418 | ||||
| 3 | 115 | 22,4 | 0,4459 | 55,42359 | ||||
| 3 | 116 | 23 | 0,4578 | 57,40301 | ||||
| 3 | 117 | 23,8 | 0,4737 | 59,38242 | ||||
| 3 | 118 | 24,6 | 0,4896 | 61,36184 | ||||
| 3 | 119 | 25,7 | 0,5115 | 63,34125 | ||||
| 3 | 120 | 26,8 | 0,5334 | 65,32067 | ||||
| 3 | 121 | 27,8 | 0,5533 | 67,30008 | ||||
| 3 | 122 | 28,9 | 0,5752 | 69,27949 | ||||
| 3 | 123 | 30,2 | 0,6011 | 71,25891 | ||||
| 3 | 124 | 31,6 | 0,6290 | 73,23832 | ||||
| 3 | 125 | 32,9 | 0,6549 | 75,21774 | ||||
| 3 | 126 | 34,5 | 0,6867 | 77,19715 | ||||
| 3 | 127 | 35,9 | 0,7146 | 79,17656 | ||||
| 3 | 128 | 35,5 | 0,7066 | 81,15598 | ||||
| 3 | 129 | 39,5 | 0,7862 | 83,13539 | ||||
| 3 | 130 | 40,7 | 0,8101 | 85,11481 | ||||
| 3 | 131 | 42,5 | 0,8459 | 87,09422 | ||||
| 3 | 132 | 44,2 | 0,8798 | 89,07363 | ||||
| 3 | 133 | 45 | 0,8957 | 91,05305 | ||||
| 4 | 134 | 0,13 | 0,0026 | 0 | ||||
| 4 | 135 | 1,4 | 0,0279 | 1,923077 | ||||
| 4 | 136 | 3,4 | 0,0677 | 3,846154 | ||||
| 4 | 137 | 5,6 | 0,1115 | 5,769231 | ||||
| 4 | 138 | 7,8 | 0,1553 | 7,692308 | ||||
| 4 | 139 | 10,4 | 0,2070 | 9,615385 | ||||
| 4 | 140 | 13 | 0,2588 | 11,53846 | ||||
| 4 | 141 | 15,6 | 0,3105 | 13,46154 | ||||
| 4 | 142 | 17,9 | 0,3563 | 15,38462 | ||||
| 4 | 143 | 20,2 | 0,4021 | 17,30769 | ||||
| 4 | 144 | 22,4 | 0,4459 | 19,23077 | ||||
| 4 | 145 | 24,6 | 0,4896 | 21,15385 | ||||
| 4 | 146 | 26,6 | 0,5295 | 23,07692 | ||||
| 4 | 147 | 27,3 | 0,5434 | 25 | ||||
| 4 | 148 | 29,9 | 0,5951 | 26,92308 | ||||
| 4 | 149 | 31,5 | 0,6270 | 28,84615 | ||||
| 4 | 150 | 39 | 0,7763 | 30,76923 | ||||
| 4 | 151 | 34,6 | 0,6887 | 32,69231 | ||||
| 4 | 152 | 35,9 | 0,7146 | 34,61538 | ||||
| 4 | 153 | 37,3 | 0,7424 | 36,53846 | ||||
| 4 | 154 | 38,7 | 0,7703 | 38,46154 | ||||
| 4 | 155 | 40 | 0,7962 | 40,38462 | ||||
| 4 | 156 | 41,4 | 0,8240 | 42,30769 | ||||
| 4 | 157 | 42,7 | 0,8499 | 44,23077 | ||||
| 4 | 158 | 44,1 | 0,8778 | 46,15385 | ||||
| 4 | 159 | 45,5 | 0,9057 | 48,07692 | ||||
| 4 | 160 | 45,8 | 0,9116 | 50 | ||||
| 4 | 161 | 40,5 | 0,8061 | 51,92308 | ||||
| 4 | 162 | 35,3 | 0,7026 | 53,84615 | ||||
| 4 | 163 | 30,6 | 0,6091 | 55,76923 | ||||
| 4 | 164 | 26,7 | 0,5314 | 57,69231 | ||||
| 4 | 165 | 22,6 | 0,4498 | 59,61538 | ||||
| 4 | 166 | 19,3 | 0,3842 | 61,53846 | ||||
| 4 | 167 | 15,6 | 0,3105 | 63,46154 | ||||
| 4 | 168 | 15,21 | 0,3027 | 65,38462 | ||||
| 4 | 169 | 12,2 | 0,2428 | 67,30769 | ||||
| 4 | 170 | 9,3 | 0,1851 | 69,23077 | ||||
| 4 | 171 | 6,5 | 0,1294 | 71,15385 | ||||
| 4 | 172 | 4,3 | 0,0856 | 73,07692 | ||||
| 4 | 173 | 2,3 | 0,0458 | 75 | ||||
| 4 | 174 | 0,5 | 0,0100 | 76,92308 | ||||
| 4 | 175 | 0,07 | 0,0014 | 78,84615 | ||||