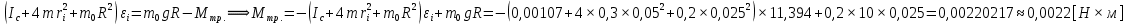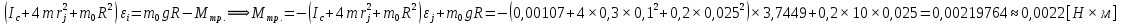МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИСанкт-Петербургский государственный электротехнический Университет «ЛЭТИ» им. В.И.Ульянова (Ленина)Кафедра ФИЗИКИотчетпо лабораторной работе №3 (№7)по дисциплине «Физика»Тема: «Маятник Обербека»
Преподаватель __________________________________________________________ Сизова Е.А.

Студент гр. 1291 _________________________________________________________ Родин В.Д.
Санкт-Петербург2021Цель работы: Экспериментальное исследование законов динамики вращательного движения твердого тела на примере маятника Обербека, определение постоянной части момента инерции маятника Обербека.Теоретические положения: 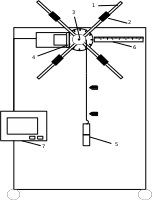Маятник Обербека представляет собой крестовину 1 с грузами 2, на вращающейся оси 3. На шкив на оси намотана нить с грузиком 5, которая, разматываясь, вызывает вращательное движение крестовины. На четырех взаимно перпендикулярных стержнях крестовины располагаются четыре подвижных груза 2 массой т каждый, положение которых относительнооси вращения маятникаопределяетсяпо измерительнойлинейке6.Вопытеположениягрузовнакрестовинеменяютспомощьюихперемещенияпо резьбовымспицамкрестовины.Фиксациягрузов в каждой серии измерений осуществляется путем законтривания двух резьбовыхполовинкаждого грузаввыбранном положении.Наосикрестовинырасполагаетсядатчик 4 угловой скорости вращения маятника,подключенныйчерезконцентраторк измерительному

---

блоку 7.

Основные формулы:

Уравнение движения твердого тела вокруг неподвижной оси имеет вид:

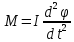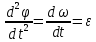, где ,где 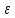-угловое ускорение тела, I-момент инерции маятника, М- момент сил, действующих на маятник. 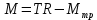, где Т- сила натяжения нити шкива, R- радиус шкива, М_тр- момент силы трения нити в оси маятника.

Момент инерции стержня является мерой его инертности при вращательном движении и зависит от расположения массы относительно его оси вращения. Определяется равенством:

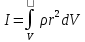, где 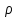- плотоность тела [кг/м³], расстояние элементарного объема dVот выбраной оси, dV-объем тела.

На маятник действуют две внешние силы: F_тр.-сила трения, и F_mg-сила тяжести грузика, массой m. Их моменты, соответственно М_тр. и М_mg, а уравнение движения имеет вид 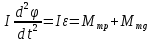. Также отметим, что непосредственно к точке крепления вращающейся оси приложена сила реакции опоры N. Её момент- M_N.

Запишем основные уравнения динамики для поступательного и вращательного движения маятника Обербека:

.

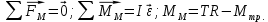для груза:

; .

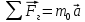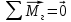Движение груза описывается: 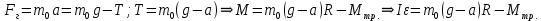, 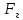- сила, действующая на грузик

Угловое ускорение вращения маятника связано с ускорением и массой груза m₀ соотношением 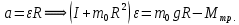т.к. правая часть неизменна, то I и 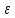связаны

Момент инерции крестовины с 4мя грузами:

---

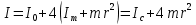
, где I₀- момент инерции крестовины без груза, 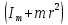- момент инерции одного груза массой m (по формуле Гюйгенса-Штейнера), I_m- собственный момент инерции груза, 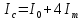- постоянная часть момента инерции для маятника Обербека

Для r_i и r_j запишем:

.
.

.

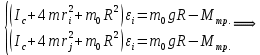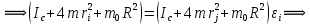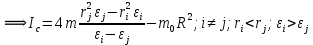При этом 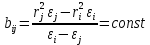при различной геометрии постановки эксперимента

Угловое ускорение вращения маятника находится по формуле 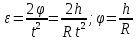– угол поворота шкива при прохождении грузом на нити расстояния h между 2мя метками за время t.

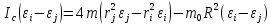-формула для расчета постоянной части момента инерции маятника Обербека

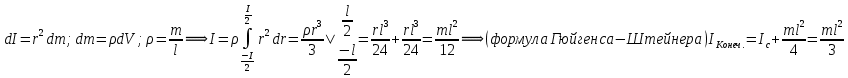, где 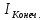-момент инерции стержня относительно его концов при оси, проходящей через его середину, 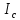- собственный момент инерции стержня

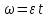-угловая скорость в момент t с учетом того, что движения равноускоренное. Тогда угол поворота 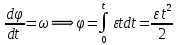. Линейная скорость связана соотношением 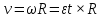, нормальное ускорение равно .

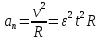Число сделанных маятником оборотов можно рассчитать по формуле

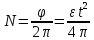
Проскальзывания нити нет (т.е. 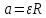), следовательно расстояние пройденное грузиком h равно: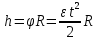

График 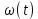и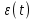 теоретически имеет приблизительный вид.

---

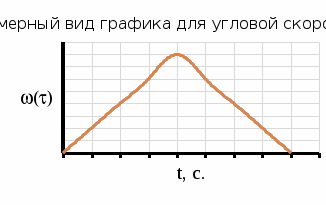
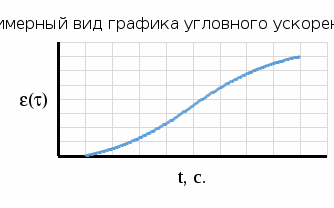
Решение:

1. 
   
   
   1. 
      Оценим значения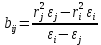
      

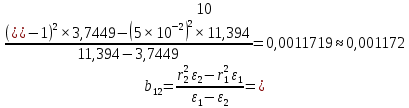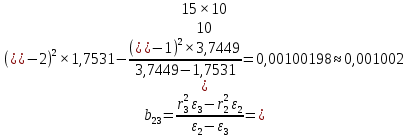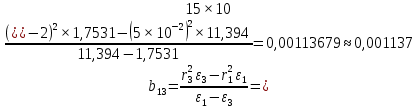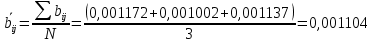. . . .Учитывая погрешность при проведении эксперимента (в т.ч. то, что электронная установка всегда выдает немного различные значения), можно считать, что значения коэффициентов имеют близкие значения.

2. 
   Измерим постоянный момент инерции. Выборочный метод. Значения приведены в единицах системы СИ
   

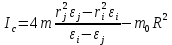-общая формула ...

3. 
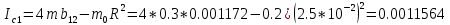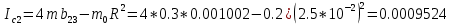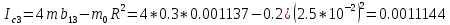   Измерение среднего (выборочный метод)
   

	1	2	3
Ic	0,0011564	0,0009524	0,0011144

Составление выборки

	1	2	3
Ic	0,0009524	0,0011144	0,0011564

Среднее значение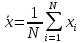; N=3, по условию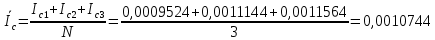.Средне-квадратическое отклонение (СКО)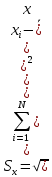; N=3 по условию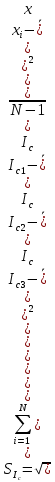.Проверка на промахи 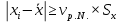, по условию v_р.N.=1,4Для 0,0009524: -

---

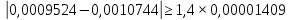0,0009524 соответствует промежутку возможных решений.Для 0,0011564: 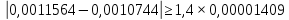- 0,0011564 соответствует промежутку возможных решений.Средне-квадратическое отклонение среднего (СКОС)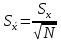; N=3 (по условию)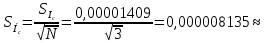0,00000814Случайная погрешность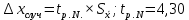(по условию)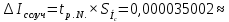0,000035Частные производные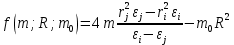..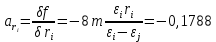..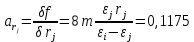.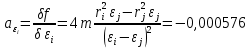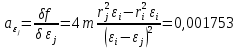Приборная погрешность 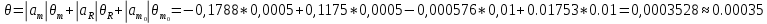.Полная доверительная погрешность 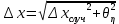..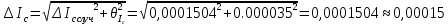Округление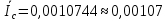.Ответ: 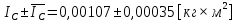, при N=3, P=95%

2. 
   
   
   1. 
      Оценим значений М_тр.
      

1. 
   
   
2. 
   
   

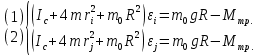
Можно сделать вывод о соответствии друг другу вычисленных значений моментов силы трения. Соответственно вычисление значения постоянной части момента инерции по формуле, использованной в п.1, возможно, значения сходны.

3. 
   
   
   1. 
      Собственный момент инерции
      

.

2. 
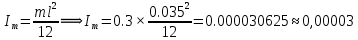   Момент инерции крестовины маятника
   

---

Смотрите также файлы

• Ход занятия.docx

• Программа курса повышения квалификации педагогов Урок математики в школе фокусы и стратегии улучшений.pdf

• Аналитическая справка Критерии и показатели эффективности региональной дорожной карты по реализации Положения о системе наставничества педагогических работников в образовательной организации.docx

• На сколько процентов следует повысить за год зарплату учителя, чтобы к концу года ее реальная величина выросла на 9 при годовой инфляции в 36% Ответ.docx

• Напоминаем, что существует официальный от фипи список дат (всеобщей истории )для второго задания егэ по истории.docx