Файл: 2. математические модели в технической диагностике Основные понятия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 95
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
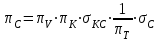.Это уравнение нелинейное и выражается через произведение сомножителей. Поэтому для его линеаризации необходимо провести сначала логарифмирование, затем дифференцирование и далее соответствующие преобразования (см. первый вариант линеаризации). Если рассматривается работа двигателя на земле, то можно считать V = const. Выполнив необходимые преобразования, получим линейное алгебраическое уравнение в относительных отклонениях:
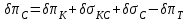.Данное уравнение устанавливает связь между относительными изменениями параметров, характеризующих техническое состояние компрессора -
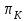, турбины - 
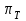, камеры сгорания - 
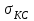, сопла - 
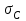. Уравнение баланса мощностей на валу двигателя устанавливает соотношение между работой турбины
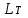, работой, потребляемой компрессором 
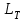, а также их коэффициентами полезного действия 
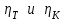. Это уравнение имеет вид 
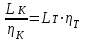.После выполнения линеаризации это уравнение в относительных изменениях параметров запишется следующим образом:
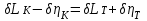.Из теории авиационных ГТД известно, что работу, создаваемую турбиной, можно выразить через газовую постоянную RГ, температуру газа ТГ, степень расширения газа на турбине Т и показатель адиабаты k следующим образом:
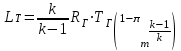.Выполнив линеаризацию этого уравнения, мы получим соотношение для относительных изменений параметров в следующем виде:
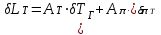.Работа, потребляемая компрессором, также может быть выражена через газовую постоянную, угловую скорость вращения U (которая прямо пропорциональна частоте вращения ротора n), степень сжатия компрессора К и показатель адиабаты:
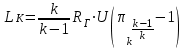.После выполнения линеаризации соотношение между относительными изменениями параметров запишется следующим образом:
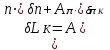.Воспользовавшись этими соотношениями, получим уравнение баланса мощностей, выраженное в относительных изменениях параметров:
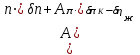
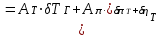.Последнее выражение устанавливает связь между параметрами, являющимися непосредственными параметрами технического состояния (степень сжатия (расширения), коэффициенты полезного действия), и измеряемыми (диагностическими) параметрами (частота вращения ротора, температура газов). Полученное уравнение является линейным алгебраическим уравнением с соответствующими коэффициентами влияния.
Подобным образом преобразуются и другие уравнения, известные из теории авиационных ГТД. В результате получаем систему алгебраических линейных уравнений, порядок которой зависит от типа двигателя и степени детализации протекающих в нем процессов [1, 10]. Уравнения включают в себя измеряемые параметры, параметры технического состояния и коэффициенты влияния. Наиболее часто в качестве параметров технического состояния (влияющих факторов) выбираются коэффициенты полезного действия и площади сечений (в первую очередь сопловых аппаратов). В качестве диагностических признаков выбираются частота вращения ротора, температура газа, расход топлива. Коэффициенты влияния определяются расчетным или экспериментальным путем. После определения коэффициентов влияния можно построить матрицу этих коэффициентов (диагностическую матрицу) или соответствующую таблицу. Полученные таблицы непосредственно используются для решения практических задач.
В качестве примера приведем фрагмент матрицы коэффициентов влияния, полученной в работе [10] для двигателя НК-8-2У (табл. 2. 12).
Таблица 2.12
| | КНД | КВД | FСА | ТВД | ТНД |
| nвд | -0,3 | 0,4 | -0,4 | 0,6 | -0,3 |
| Gт | -1,0 | -0,4 | 0,2 | -0,5 | -1,2 |
В этой таблице в качестве диагностических параметров представлены частота вращения ротора высокого давления nВД и расход топлива GT. В качестве параметров технического состояния представлены коэффициенты полезного действия компрессоров низкого и высокого давлений КНД и КВД , турбин низкого и высокого давлений ТНД и ТВД , а также площадь соплового аппарата турбины высокого давления FСА.
Одним из простейших методов анализа подобных таблиц является «метод знаков». Знак "–" у коэффициента влияния свидетельствует о том, что диагностический параметр изменяется в противоположную сторону относительно влияющего фактора, знак "+" свидетельствует о том, что они изменяются в одну сторону.
Из данной таблицы видно, что если в процессе эксплуатации обнаруживается снижение nнд, но GТ увеличивается, то можно с уверенностью сказать, что наблюдается прогар соплового аппарата. В других случаях разделить дефекты турбины и компрессора таким способом затруднительно.
Для решения этой задачи необходимы приемы, позволяющие разделить дефекты компрессора и турбины. Простейшим приемом является увеличение числа диагностических параметров. Если количество параметров будет достаточным, то можно заменить положительные значения коэффициентов влияния на 1, а отрицательные – на 0 и получим таблицу, аналогичную таблице состояний. Однако увеличение числа измеряемых параметров не всегда позволяет решить задачу разделения технических состояний.
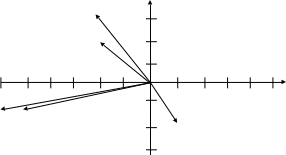
Другим возможным вариантом решения задачи диагностики является использование той информации, которая заложена в величине диагностического параметра. Например, данные табл. 2.12 можно отобразить на плоскости с координатами nВД и GТ , то есть представить в двухмерном пространстве диагностических признаков (рис.2.18).
nВД ТВД 0,6
КВД 0,4
0,2
-1,2 -1,0 -0,8 -0,6 -0,4 -0,2 0,2 0,4 0,6 0,8 GT
ТНД -0,2
КНД F
-0,4
-0,6
Рис.2.18. Отражение таблицы коэффициентов влияния на плоскости
диагностических параметров
В таком случае все технические состояния (диагнозы) представляются в виде точки в пространстве диагностических (измеряемых) параметров. Если для данного примера сформировать диагностические признаки в виде модуля вектора, соединяющего начало координат с точкой диагноза и угла наклона этого вектора к одной из осей, то эти признаки позволяют разделить указанные технические состояния. Существуют и другие методы использования числовых значений коэффициентов влияния или непосредственно диагностических параметров для решения задач распознавания технических состояний (распознавания диагнозов) [1, 2, 9, 14, 29, 31].
В данной главе мы рассмотрели наиболее распространенные виды математических (диагностических) моделей, которые применяются при решении практических задач диагностики технического состояния объектов авиационной техники. Изложенный материал позволяет сделать некоторые выводы.
Математические модели позволяют:
1.Дать формализованное описание связи технического состояния (параметров технического состояния) с выходными (диагностическими) параметрами объекта диагностики.
2.Выделить из бесконечного множества технических состояний объекта диагностики конечный набор диагнозов, которые следует диагностировать, и дать формализованное описание этих технических состояний (диагнозов).
3.Обосновать выбор диагностических (выходных) параметров объекта, для которых следует проводить измерения при выполнении процедур определения технического состояния.
4.Сформировать диагностические признаки, которые должны использоваться в процессе диагностирования.
В заключение отметим, что в ряде случаев создание диагностической модели завершается разработкой таблицы состояний или может быть сведено к подобной таблице. Тогда задача определения технического состояния решается путем непосредственного применения этой таблицы.
В большинстве случаев такой подход не удается реализовать. Как правило, результатом создания диагностической модели является выбор диагностических параметров или признаков. При этом важное значение имеет эффективность выбранных диагностических параметров или признаков. Эффективность диагностических признаков оценивается так называемой диагностической ценностью признаков.