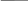
вал лопатка
Рис.2.15. Схема балки с трещиной
Будем считать, что балка совершает колебания по первой (определяющей) форме, которая на рисунке изображена пунктирной линией. При колебаниях «берега» трещины будут то сжиматься (при сжатии), то разжиматься (при растяжении). Очевидно, что при сжатии материал ведет себя как сплошной. При растяжении, поскольку «берега» трещины раскрываются, жесткость балки уменьшается, так как трещина не работает на растяжение. Таким образом, изделие с трещиной имеет различные жесткости в направлениях сжатия и растяжения. Ранее отмечалось, что жесткость определяет динамические свойства (собственную частоту) системы. Следовательно, у изделия с трещиной изменится собственная частота системы, поскольку она определяется соотношением жесткости и массы (см. формулу 2.16).

Так как мы рассматриваем колебания балки по первой (определяющей) форме колебаний, то смоделируем ее одномассовой системой с соответствующими параметрами (собственная частота системы должна быть равна собственной частоте исследуемой балки). Для упрощения рассмотрения не будем учитывать демпфирование в системе. Одномассовая система, моделирующая балку без трещины при принятых допущениях, представлена на рис.2.16. Свободные колебания этой системы описываются дифференциальным уравнением следующего вида: mx+Cx = 0, которое преобразуется в выражение

m x(t)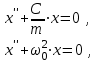

---

(2.17)

C где 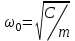- собственная частота

системы.

Рис.2.16

Определим начальные условия для момента времени t = 0. Будем считать, что для начального момента времени координата центра тяжести массы равна нулю (x=0), а его скорость имеет конечное значение V₀ ( 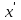= V₀). Уравнение свободных колебаний без демпфирования при наличии в начальный момент скорости определяется следующим уравнением:

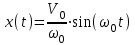. (2.18)
Из этого уравнения следует, что при отсутствии трещины свободные колебания совершаются с частотой, равной собственной частоте системы.

Изменим систему, изображенную на рис.2.16, таким образом, чтобы она отражала изменение динамических характеристик при появлении трещины. Наличие трещины учтем добавочной пружиной С_ДОБ (рис.2.17). С_ДОБ - жесткость, которая учитывается только при сжатии (при x < 0).




х(t)

m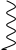

С₀ - жёсткость неповреждённого участка вала;

С₀ С_ДОБ - жесткость вала, которая добавляется

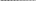
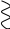x(t) = 0 при закрытии трещины.

С_ДОБ



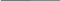
Рис. 2.17. Схема системы, имитирующей трещину

Жёсткость С₀ работает и на растяжение, и на сжатие. Она моделирует жесткость неповреждённого участка вала. В первом приближении можно считать, что отношение добавочной жесткости к основной жесткости равно отношению длины трещины 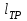к характерному размеру изделия (например, лопатки) 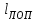в направлении трещины: 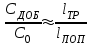. Следовательно, в реальной ситуации 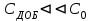. Введем следующие обозначения

---

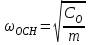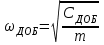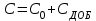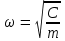; ; ; . В силу 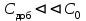имеем   _осн .

С учетом принятых обозначений и допущений свободные колебания системы, изображенной на рис.2.17, будут описываться следующими уравнениями
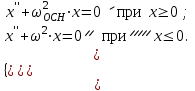(2.19)
При задании начальных условий t = 0 ; x = 0; 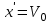можно получить решение этих уравнений. Решение будет периодической функцией с периодом Т  . Время будет изменяться в интервале от -  до _осн. Решение дифференциальных уравнений (2.23) в указанном временном интервале будет иметь следующий вид:

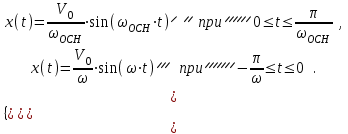(2.20)
Функция, заданная уравнениями (2.20), несимметрична относительно начала координат. Справа и слева от начала координат несколько отличаются амплитуды и частоты колебаний. Применим к функции x(t) разложение в ряд Фурье, что позволит представить ее в виде суммы отдельных гармонических составляющих:
,

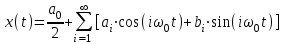где 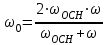, а коэффициенты ряда Фурье а_i и b_i определяются известными соотношениями

,

.

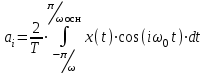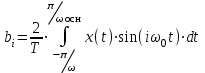Из анализа последних трех выражений следует, что свободные колебания системы, изображенной на рис. 2.17, не являются гармоническими и содержат несколько составляющих. Например, для значения i = 1 будем иметь а₁ = 0 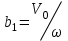. Для значения i = 2 соответственно получим следующие значения: a₂ = 0; .

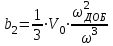Отсюда отношение амплитуд второй и первой гармонических составляющих будет выражаться следующим уравнением:

.

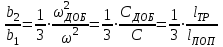Обобщая полученные результаты, можно сделать следующие выводы:

1.При появлении трещины свободные колебания системы становятся негармоническими, в

---

сигнале присутствуют высшие гармоники, в частности, вторая гармоника.

2. Отношение амплитуды второй (верхней) гармоники к амплитуде первой (основной) гармоники равно 1/3 отношения размера трещины к характерному размеру изделия.

3. Основная частота свободных колебаний изделия с трещиной меньше частоты свободных колебаний изделия без трещины, поскольку 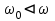_осн .

В заключение следует отметить, что аналитические модели в виде дифференциальных уравнений применяются не только в вибрационной диагностике. Они используются также, например, в методах диагностирования по температурным полям.

Кроме дифференциальных уравнений аналитические модели могут быть представлены алгебраическими уравнениями [1, 10, 27, 31, 41].

---

2.6 Аналитические модели на основе алгебраических уравнений
Если связь между входным возмущением, внутренними параметрами объекта диагностирования и выходными диагностическими параметрами представлена в виде алгебраического уравнения или системы алгебраических уравнений, то мы имеем аналитическую модель алгебраического вида. В зависимости от физического характера объекта диагностирования алгебраические уравнения могут быть линейными или нелинейными. В простейшем случае при описании объекта диагностики подобными моделями задается система линейных алгебраических уравнений, в которых количество уравнений равно числу неизвестных параметров технического состояния или числу диагнозов (то есть числу выбранных для диагноза технических состояний).

Рассмотрим случай представления моделей в виде системы линейных алгебраических уравнений. В общем виде
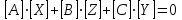. (2.21)
В этом уравнении X , Z, Y соответственно вектор входных возмущений, действующих на объект, вектор внутренних параметров объекта, вектор выходных диагностических параметров. Матрицы А , В , С являются матрицами коэффициентов уравнения.

При проведении диагностирования, как правило, располагают значениями диагностических параметров (т.е. известен вектор [Y]), по которым необходимо определить значения входных или внутренних параметров (т.е. определить векторы [X] или [Z]). С точки зрения математического решения задачи диагностики между векторами входных параметров [Х] и вектором внутренних параметров [Z] нет различий. Поэтому векторы [Х] и [Z] можно объединить в общий вектор [R], который называется вектором влияющих факторов, и тогда уравнение (2.21) примет вид

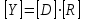. (2.22)
Вектор 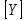c компонентами y_i называют еще вектором отклика системы на вектор возмущающих факторов [R] с компонентами r_j.

Большинство линейных моделей, приведенных к окончательному виду, разрешены относительно выходных диагностических параметров (откликов) и описываются системой уравнений вида (2.26). Каждое отдельное уравнение в этой системе представляет собой зависимость одного отклика от нескольких влияющих факторов.

В большинстве случаев для задач диагностики имеют

---

Смотрите также файлы

• Футбо л.pptx

• Решение 43 00021 00022 000 ущерб страхователя 22 00070%15 400 сумма страхового возмещения.docx

• Основные понятия теории инноватики.docx

• Пн 15. 04. 2021 аза тілі мен дебиеті 4 А,Б сыныптар Малімні аты.docx

• Специальная физическая подготовка.docx