Файл: 2. математические модели в технической диагностике Основные понятия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 97
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х1
 х2 Qi yi
х2 Qi yi
 х3
х3

Рис.2.1. Элемент функциональной модели
Количество входов определяется числом внешних воздействий на конкретный элемент. Связи между элементами обозначаются линиями со стрелками, указывающими направление прохождения сигнала. Считается, что в объекте может выходить из строя только один функциональный элемент. При этом i - е неисправное состояние идентифицируется с отказом i - блока. В этой ситуации запись состояния s представляется в виде вектора S( ), в котором количество координат соответствует количеству блоков. Значения координат задаются в соответствии со следующими правилами: если блок исправен, то координата равна 1, а если блок неисправен, то координата равна 0. Например, если объект диагностики имеет пять блоков, то исправное состояние запишем вектором S0(1 1 1 1 1), при неисправном первом блоке техническое состояние запишется следующим вектором S1 (0 1 1 1 1 ).
Под проверкой j понимается операция по оценке выходных сигналов всех блоков объекта при нахождении его в состоянии si . При наличии в объекте диагностики n функциональных блоков общее количество технических состояний равно n +1 (n неисправных и одно исправное), а количество проверок равно n.
При формальном описании результатов j-й проверки Rij отдельного элемента функциональной схемы при нахождении объекта в i-м состоянии принимаются следующее правила:
1. Результат принимается = 1, если блок исправен и на его входы подаются допустимые воздействия.
2. Результат принимается = 0, если на входы блока подаются допустимые воздействия, а он неисправен.
3. Результат принимается = 0, если блок исправен, но хотя бы на один его вход подается недопустимое воздействие.
Пользуясь таким представлением, можно задать все множество технических состояний объекта, множество проверок, множество результатов и составить таблицу состояний.
Рассмотрим пример построения таблицы состояний объекта диагностики, который можно представить функциональной моделью, состоящей из шести элементов (рис.2.2).







 x 1 Q 1 y1 Q 2 y 2 Q 3 y3
x 1 Q 1 y1 Q 2 y 2 Q 3 y3




 x 2 Q 4 y 4 Q5 y 5 Q 6 y6
x 2 Q 4 y 4 Q5 y 5 Q 6 y6





Рис. 2.2. Пример функциональной шестиэлементной модели
Для такой модели количество технических состояний равно семи. Исправное состояние можно представить шестимерным вектором S0(1 1 1 1 1 1), при отказе блока Q1 техническое состояние представим вектором S1(0 1 1 1 1 1) и т.д. Поскольку в объекте шесть блоков, то для проверки функционирования каждого блока необходимо проверить его выходной сигнал. Следовательно, количество необходимых проверок равно шести. Будем считать, что при проведении каждой из проверок j (j = 1. . . 6) на вход модели подаются входные воздействия x1 и x2, которые принимают только допустимые значения. В то же время выходные сигналы блоков yi (i = 1. . . 6) могут принимать как допустимые, так и недопустимые значения. Допустимое значение выходной сигнал принимает в случае, если блок исправен и на его входы подаются допустимые воздействия. Недопустимое значение выходной сигнал принимает в двух случаях: если блок исправен, но на его входы подаются недопустимые сигналы, или если входные сигналы принимают допустимые значения, но блок неисправен.
С учетом этого и пользуясь изложенными выше тремя правилами результат элементарной проверки блоков объекта, находящегося в i-м техническом состоянии (отказ i-го блока), будем принимать равным 1, если сигнал на выходе проверяемого блока принимает допустимое значение, и равным 0, если сигнал на выходе проверяемого блока принимает недопустимое значение. Например, при отказе блока Q2 нулевые значения примут результаты R22, R23, R26, поскольку при проведении элементарных проверок 2 , 3 , 6 для блоков Q2, Q3, Q6 выходные сигналы примут недопустимые значения. Воспользовавшись приведенными выше рассуждениями, составим табл.2.2 состояний для объекта, функциональная модель которого изображена на рис.2.2.
Таблица 2.2
Таблица состояний для шестиэлементного объекта
Полученная таблица является как проверяющей, так и разделяющей, т.е. позволяет решать задачи контроля и диагностики.
Непременным условием применения функциональной модели является наличие у всех элементов (блоков) объекта диагностирования одного выхода. В реальных условиях выходной сигнал некоторых блоков объекта контроля может характеризоваться несколькими параметрами. В этом случае считается, что блок имеет несколько выходных сигналов, каждый их которых характеризует соответствующий параметр. В такой ситуации применяют так называемое «расщепление» выходов. Рассмотрим применение этого приема на примере.
На рис. 2.3 изображена схема системы электроснабжения самолета.

IВ РН





 nДВ ППО nППО СГС u БЗУ U
nДВ ППО nППО СГС u БЗУ U


 f
f
If РЧ
Рис. 2.3. Схема системы электроснабжения самолета:
ППО - привод постоянных оборотов; СГС - синхронный генератор самолетный; РН - регулятор напряжения; РЧ - регулятор частоты; БЗУ - блок защиты и управления; nДВ - частота вращения коробки приводов двигателя; nППО - частота вращения генератора; u и f - напряжение и частота на выходе генератора; Iв - ток возбуждения генератора; If - управляющее воздействие по частоте на ППО; U - напряжение, подаваемое в самолетную сеть.
Выходной сигнал генератора характеризуется двумя параметрами: напряжением и частотой. При составлении функциональной модели проводится «расщепление» выходного сигнала генератора по следующим правилам.
Правило первое. Если выходной сигнал характеризуется несколькими параметрами, то выходной сигнал «расщепляется» на количество сигналов, равное количеству параметров.
Схема системы электроснабжения с «расщепленным» выходным сигналом генератора представлена на рис.2.4.
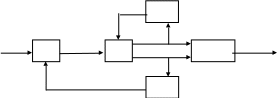
IВ РН
nДВ ППО nППО СГС u БЗУ U
f
If РЧ
Рис. 2.4. Схема с «расщепленным» выходным сигналом генератора
В соответствии с этой схемой один из блоков (генератор) объекта диагностирования имеет два выхода, что не может быть в функциональной модели. Для приведения в соответствие количества выходов блоков с требова-нием функциональной модели пользуются вторым правилом.
Правило второе. Если i-й блок имеет несколько выходов, то на функциональной модели он заменяется несколькими блоками, имеющими только один выход. Число блоков равно числу выходов «расщепляемого» блока.
С учетом этого правила предыдущую схему представим следующим образом
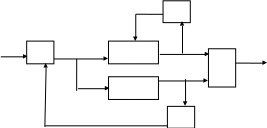
IВ РН
nДВ ППО nППО СГС №1 u U
БЗУ
СГС №2 f
If РЧ
Рис. 2.5. Схема с «расщепленным» выходом генератора
Приведенная схема соответствует требованиям функциональной модели, что позволяет изобразить модель в принятых ранее обозначениях (рис.2.6).
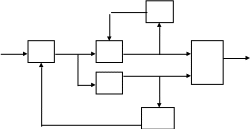
y4 Q 4
x Q 1 y1 Q 2 y2 Q 6 y6
Q 3 y3
y5 Q 5
Рис. 2.6. Функциональная модель системы электроснабжения самолета
Пользуясь этой моделью, можно составить табл.2.3 состояний. Таблица состояний заполняется исходя из следующих соображений. При исправном состоянии всех блоков сигналы на их выходах будут принимать допустимые значения, то есть результаты всех проверок будут равны 1. При отказе первого блока на выходе всех блоков сигналы будут принимать недопустимые значения, то есть результаты всех проверок будут равны 0. При отказе блока №2 недопустимые значения выходных сигналов будут у блоков №2, №4 и №6, то есть результаты проверок этих блоков будут равны 0. Для остальных блоков результаты проверок будут равны 1. На основе подобных рассуждений заполняется вся таблица.
Таблица 2.3
Таблица состояний системы электроснабжения
 х2 Qi yi
х2 Qi yi  х3
х3 
Рис.2.1. Элемент функциональной модели
Количество входов определяется числом внешних воздействий на конкретный элемент. Связи между элементами обозначаются линиями со стрелками, указывающими направление прохождения сигнала. Считается, что в объекте может выходить из строя только один функциональный элемент. При этом i - е неисправное состояние идентифицируется с отказом i - блока. В этой ситуации запись состояния s представляется в виде вектора S( ), в котором количество координат соответствует количеству блоков. Значения координат задаются в соответствии со следующими правилами: если блок исправен, то координата равна 1, а если блок неисправен, то координата равна 0. Например, если объект диагностики имеет пять блоков, то исправное состояние запишем вектором S0(1 1 1 1 1), при неисправном первом блоке техническое состояние запишется следующим вектором S1 (0 1 1 1 1 ).
Под проверкой j понимается операция по оценке выходных сигналов всех блоков объекта при нахождении его в состоянии si . При наличии в объекте диагностики n функциональных блоков общее количество технических состояний равно n +1 (n неисправных и одно исправное), а количество проверок равно n.
При формальном описании результатов j-й проверки Rij отдельного элемента функциональной схемы при нахождении объекта в i-м состоянии принимаются следующее правила:
1. Результат принимается = 1, если блок исправен и на его входы подаются допустимые воздействия.
2. Результат принимается = 0, если на входы блока подаются допустимые воздействия, а он неисправен.
3. Результат принимается = 0, если блок исправен, но хотя бы на один его вход подается недопустимое воздействие.
Пользуясь таким представлением, можно задать все множество технических состояний объекта, множество проверок, множество результатов и составить таблицу состояний.
Рассмотрим пример построения таблицы состояний объекта диагностики, который можно представить функциональной моделью, состоящей из шести элементов (рис.2.2).







 x 1 Q 1 y1 Q 2 y 2 Q 3 y3
x 1 Q 1 y1 Q 2 y 2 Q 3 y3 



 x 2 Q 4 y 4 Q5 y 5 Q 6 y6
x 2 Q 4 y 4 Q5 y 5 Q 6 y6




Рис. 2.2. Пример функциональной шестиэлементной модели
Для такой модели количество технических состояний равно семи. Исправное состояние можно представить шестимерным вектором S0(1 1 1 1 1 1), при отказе блока Q1 техническое состояние представим вектором S1(0 1 1 1 1 1) и т.д. Поскольку в объекте шесть блоков, то для проверки функционирования каждого блока необходимо проверить его выходной сигнал. Следовательно, количество необходимых проверок равно шести. Будем считать, что при проведении каждой из проверок j (j = 1. . . 6) на вход модели подаются входные воздействия x1 и x2, которые принимают только допустимые значения. В то же время выходные сигналы блоков yi (i = 1. . . 6) могут принимать как допустимые, так и недопустимые значения. Допустимое значение выходной сигнал принимает в случае, если блок исправен и на его входы подаются допустимые воздействия. Недопустимое значение выходной сигнал принимает в двух случаях: если блок исправен, но на его входы подаются недопустимые сигналы, или если входные сигналы принимают допустимые значения, но блок неисправен.
С учетом этого и пользуясь изложенными выше тремя правилами результат элементарной проверки блоков объекта, находящегося в i-м техническом состоянии (отказ i-го блока), будем принимать равным 1, если сигнал на выходе проверяемого блока принимает допустимое значение, и равным 0, если сигнал на выходе проверяемого блока принимает недопустимое значение. Например, при отказе блока Q2 нулевые значения примут результаты R22, R23, R26, поскольку при проведении элементарных проверок 2 , 3 , 6 для блоков Q2, Q3, Q6 выходные сигналы примут недопустимые значения. Воспользовавшись приведенными выше рассуждениями, составим табл.2.2 состояний для объекта, функциональная модель которого изображена на рис.2.2.
Таблица 2.2
Таблица состояний для шестиэлементного объекта
| \ s | S0 111111 | S1 011111 | S2 101111 | S3 110111 | S4 111011 | S5 111101 | S6 111110 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Полученная таблица является как проверяющей, так и разделяющей, т.е. позволяет решать задачи контроля и диагностики.
Непременным условием применения функциональной модели является наличие у всех элементов (блоков) объекта диагностирования одного выхода. В реальных условиях выходной сигнал некоторых блоков объекта контроля может характеризоваться несколькими параметрами. В этом случае считается, что блок имеет несколько выходных сигналов, каждый их которых характеризует соответствующий параметр. В такой ситуации применяют так называемое «расщепление» выходов. Рассмотрим применение этого приема на примере.
На рис. 2.3 изображена схема системы электроснабжения самолета.

IВ РН





 nДВ ППО nППО СГС u БЗУ U
nДВ ППО nППО СГС u БЗУ U

 f
fIf РЧ
Рис. 2.3. Схема системы электроснабжения самолета:
ППО - привод постоянных оборотов; СГС - синхронный генератор самолетный; РН - регулятор напряжения; РЧ - регулятор частоты; БЗУ - блок защиты и управления; nДВ - частота вращения коробки приводов двигателя; nППО - частота вращения генератора; u и f - напряжение и частота на выходе генератора; Iв - ток возбуждения генератора; If - управляющее воздействие по частоте на ППО; U - напряжение, подаваемое в самолетную сеть.
Выходной сигнал генератора характеризуется двумя параметрами: напряжением и частотой. При составлении функциональной модели проводится «расщепление» выходного сигнала генератора по следующим правилам.
Правило первое. Если выходной сигнал характеризуется несколькими параметрами, то выходной сигнал «расщепляется» на количество сигналов, равное количеству параметров.
Схема системы электроснабжения с «расщепленным» выходным сигналом генератора представлена на рис.2.4.

IВ РН
nДВ ППО nППО СГС u БЗУ U
f
If РЧ
Рис. 2.4. Схема с «расщепленным» выходным сигналом генератора
В соответствии с этой схемой один из блоков (генератор) объекта диагностирования имеет два выхода, что не может быть в функциональной модели. Для приведения в соответствие количества выходов блоков с требова-нием функциональной модели пользуются вторым правилом.
Правило второе. Если i-й блок имеет несколько выходов, то на функциональной модели он заменяется несколькими блоками, имеющими только один выход. Число блоков равно числу выходов «расщепляемого» блока.
С учетом этого правила предыдущую схему представим следующим образом

IВ РН
nДВ ППО nППО СГС №1 u U
БЗУ
СГС №2 f
If РЧ
Рис. 2.5. Схема с «расщепленным» выходом генератора
Приведенная схема соответствует требованиям функциональной модели, что позволяет изобразить модель в принятых ранее обозначениях (рис.2.6).

y4 Q 4
x Q 1 y1 Q 2 y2 Q 6 y6
Q 3 y3
y5 Q 5
Рис. 2.6. Функциональная модель системы электроснабжения самолета
Пользуясь этой моделью, можно составить табл.2.3 состояний. Таблица состояний заполняется исходя из следующих соображений. При исправном состоянии всех блоков сигналы на их выходах будут принимать допустимые значения, то есть результаты всех проверок будут равны 1. При отказе первого блока на выходе всех блоков сигналы будут принимать недопустимые значения, то есть результаты всех проверок будут равны 0. При отказе блока №2 недопустимые значения выходных сигналов будут у блоков №2, №4 и №6, то есть результаты проверок этих блоков будут равны 0. Для остальных блоков результаты проверок будут равны 1. На основе подобных рассуждений заполняется вся таблица.
Таблица 2.3
Таблица состояний системы электроснабжения
| \ S | S0 | S1 | S2 | S3 | S4 | S5 | S6 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |