Файл: Тема Построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 798
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
© К. Поляков, 2022
22 (повышенный уровень, время – 7 мин)
Тема: Построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы
Что проверяется:
Умение анализировать алгоритм, содержащий ветвление и цикл
3.1.1. Программная и аппаратная организация компьютеров и компьютерных систем. Виды программного обеспечения.
1.3.2. Оценивать скорость передачи и обработки информации.
Что нужно знать:
-
процессы в современных компьютерах могут выполняться параллельно, если являются независимыми -
выражение «процесс В зависит от процесса А» означает, что выполнение процесса В не может начаться раньше, чем выполнение процесса А
Пример задания:
P-00 (демо-2022). В файле 22-0.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1; 2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
Решение (электронные таблицы):
-
таблица имеет вид:
ID процесса B
Время выполнения процесса B (мс)
ID процесса (ов) A
1
4
0
2
3
0
3
1
1; 2
4
7
3
5
6
3
6
3
5
7
1
4; 6
8
2
7
9
7
0
10
8
0
11
6
9
12
6
10
-
отсортируем данные в таблице так, чтобы:
– все независимые процессы оказались в начале таблицы
– любой процесс был расположен ПОСЛЕ всех процессов, от которых он зависит
| ID процесса B | Время выполнения процесса B (мс) | ID процесса (ов) A |
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 9 | 7 | 0 |
| 10 | 8 | 0 |
| 3 | 1 | 1; 2 |
| 4 | 7 | 3 |
| 5 | 6 | 3 |
| 6 | 3 | 5 |
| 7 | 1 | 4; 6 |
| 8 | 2 | 7 |
| 11 | 6 | 9 |
| 12 | 6 | 10 |
-
добавляем еще один столбец: время окончания процесса; для всех независимых процессов записываем в соответствующие ячейки время окончания, равное длительности процесса:
ID процесса B
Время выполнения процесса B (мс)
ID процесса (ов) A
Время окончания T, мс
1
4
0
4
2
3
0
3
9
7
0
7
10
8
0
8
3
1
1; 2
4
7
3
5
6
3
6
3
5
7
1
4; 6
8
2
7
11
6
9
12
6
10
-
для остальных процессов определяем время окончания как сумму длительности этого процесса и максимального времени окончания процессов, от которых зависит данный процесс (здесь T(x) обозначает время окончания процесса с идентификатором x):
T(3) = 1 + max( T(1), T(2) ) = 1 + 4 = 5
T(4) = 7 + T(3) = 7 + 5 = 12
T(5) = 6 + T(3) = 6 + 5 = 11
T(6) = 3 + T(5) = 3 + 11 = 14
T(7) = 1 + max( T(4), T(6) ) = 1 + 14 = 15
T(8) = 2 + T(7) = 2 + 15 = 17
T(11) = 6 + T(9) = 6 + 7 = 13
T(12) = 6 + T(10) = 6 + 8 = 14
| ID процесса B | Время выполнения процесса B (мс) | ID процесса (ов) A | Время окончания T, мс |
| 1 | 4 | 0 | 4 |
| 2 | 3 | 0 | 3 |
| 9 | 7 | 0 | 7 |
| 10 | 8 | 0 | 8 |
| 3 | 1 | 1; 2 | 5 |
| 4 | 7 | 3 | 12 |
| 5 | 6 | 3 | 11 |
| 6 | 3 | 5 | 14 |
| 7 | 1 | 4; 6 | 15 |
| 8 | 2 | 7 | 17 |
| 11 | 6 | 9 | 13 |
| 12 | 6 | 10 | 14 |
-
время завершения совокупности всех процессов равно времени завершения последнего из них, поэтому нужно выбрать максимальное значение в последнем столбце -
Ответ: 17.
Решение (электронные таблицы, функция ВПР, Информатик БУ):
-
Для начала отсортируем таблицу по столбцу C (ID процесса (ов) A). Это нужно для того, чтобы отдельно рассмотреть независимые процессы (те, у которых в столбце C находится значение 0); вместо этого можно было бы использовать функцию ЕСЛИ, но в этом случае формула была бы немного сложнее;
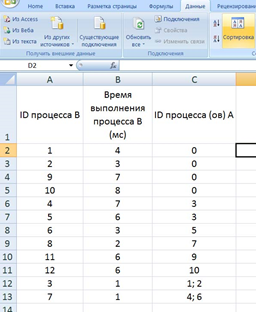
-
Теперь необходимо расцепить процессы в ячейках столбца C, в которых находится более одного процесса; в данном примере это можно было бы сделать вручную, но ручной способ не подойдет для больших таблиц. Для этого выделяем нужные ячейки столбца C, переходим в меню «Данные», и нажимаем кнопку «Текст по столбцам»:
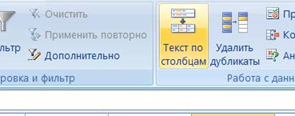
В появившемся окне выбираем формат данных «с разделителями», нажимаем кнопку «Далее», и указываем символы, которые разделяют процессы в ячейках. В нашем случае это точка с запятой и пробел. Нажимаем кнопку «Готово».
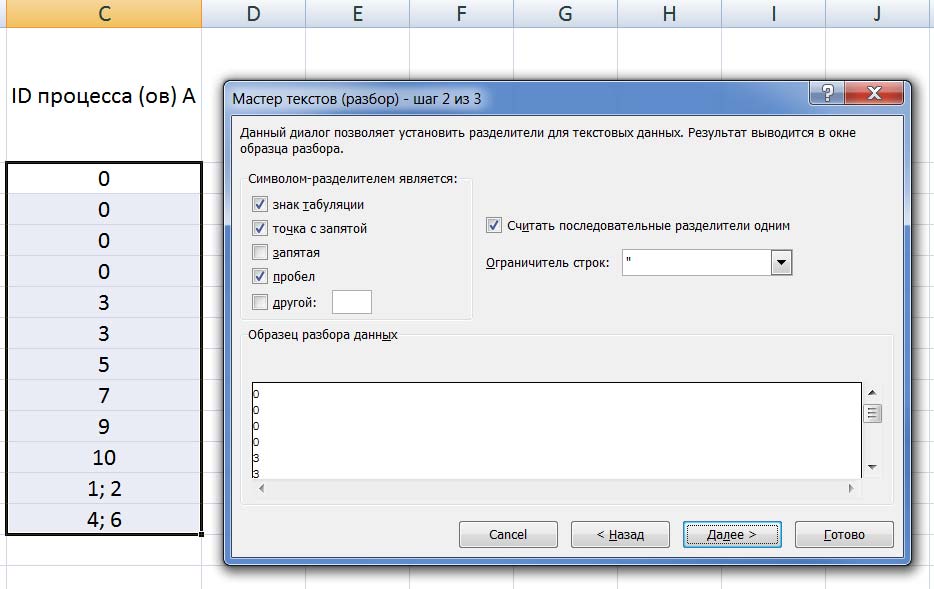
После этого один из процессов останется в столбце C, а второй отправится в столбец D (если процессов больше, чем 2, номера оставшихся размещаются в столбцах E, F и далее).
-
Посчитаем в столбце E полное время выполнения каждого процесса (время самого процесса + время процессов, связанных с ним). Сначала отдельно рассмотрим независимые процессы. Для этого в ячейке E2 пишем формулу =B2, и копируем её для всех независимых процессов.
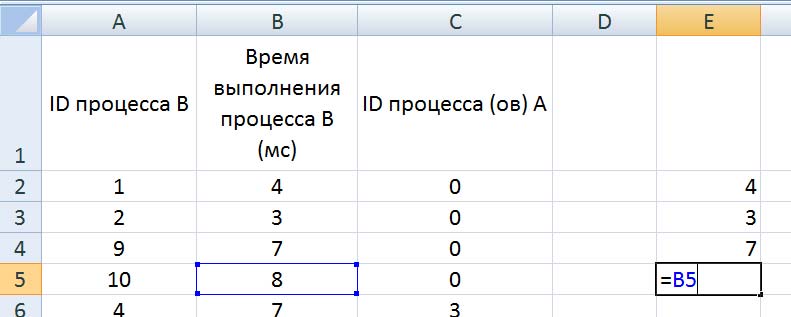
-
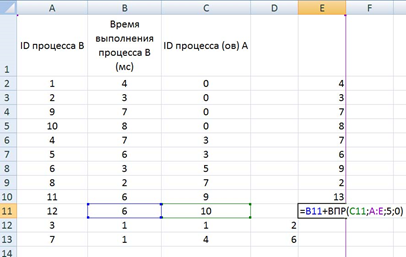
Теперь рассмотрим процессы B, которые зависят только от одного процесса. Для этого возьмем время выполнения самого процесса B, и прибавим к нему полное время выполнения процесса A (ID процесса A находится в столбце C, а полное время выполнения – в столбце E). Для поиска времени выполнения процесса A воспользуемся функцией ВПР. В ячейку E6 запишем формулу:
=B6+ВПР(C6;A:E;5;0)
и скопируем её для всех процессов B, у которых указан только один процесс A.
-
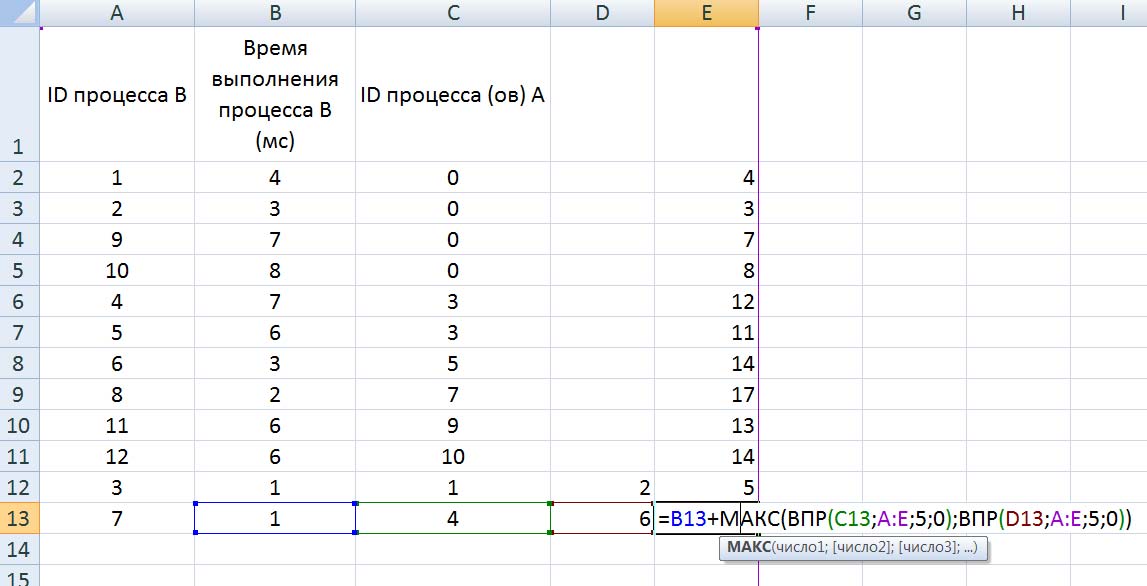
Далее рассмотрим процессы B, которые зависят уже от двух процессов. Так как процессы в столбцах C и D могут выполняться параллельно, будем брать максимальное значение среди времени их выполнения, и прибавлять к этому значению время выполнения самого процесса B. Для этого в ячейку E12 запишем формулу:
=B12+МАКС(ВПР(C12;A:E;5;0);ВПР(D12;A:E;5;0))
и копируем её для всех процессов B, у которых указано два процесса A.
-
Так мы получили столбец E, в ячейках которого указано полное время выполнения каждого процесса B. Так как процессы могут выполняться параллельно, нам остаётся найти максимальное значение в ячейках столбца E. Для этого в любую пустую ячейку пишем формулу: =МАКС(A:A) и получаем ответ: 17. -
Ответ: 17.
Решение (электронная таблица, С. Кох):
-
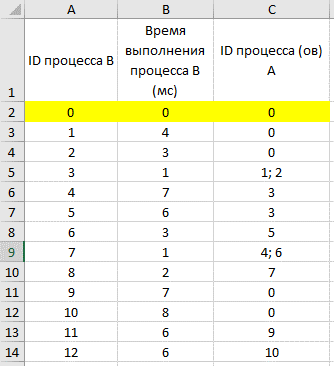
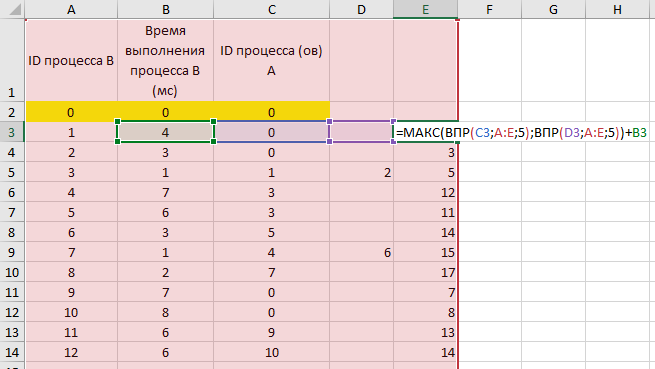
сортируем таблицу по первому столбцу (ID процесса B) и добавляем первой строкой (в электронной таблице – в строку 2) фиктивный процесс в которую записываем процесс с ID = 0, время выполнения 0 и время окончания процесса 0:
-
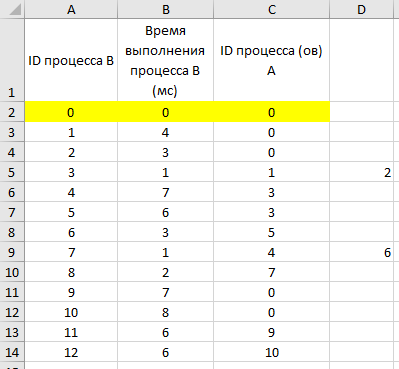
расцепляем процессы в ячейках столбца C с помощью функции «Текст по столбцам» (см. выше в решении Информатика БУ):
-
В первом свободном столбце в 3-й строке пишем формулу, которая учитывает максимальное количество процессов, которое встречается в этой задаче (например, здесь в E3 пишем формулу =МАКС(ВПР(C3;A:E;5);ВПР(D3;A:E;5))+B3)
и растягиваем эту формулу на весь столбец. В этом случае все пустые ячейки Excel считает равными 0 и обращается к 0 процессу, время завершения которого 0.
-
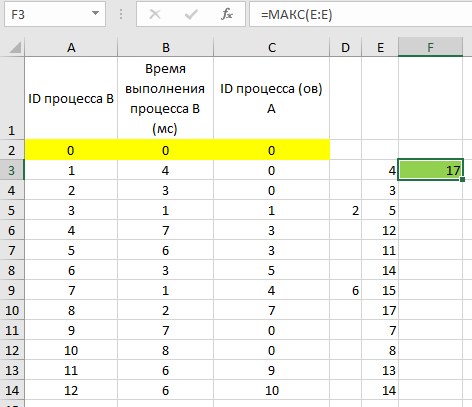
находим максимум в последнем столбце:
-
Ответ: 17.
Решение (диаграмма Ганта, А. Кожевникова):
-
Решение удобно выполнять в Excel, построив диаграмму Ганта, которая показывает зависимость процессов. Построение диаграммы состоит в закрашивании ячеек таблицы Excel разным цветом, длина (количество закрашиваемых ячеек) процесса соответствует времени его выполнения. -
Построим диаграмму Ганта для таблицы, приведённой в задании:
ID процесса B
Время выполнения процесса B (мс)
ID процесса (ов) A
1
4
0
2
3
0
3
1
1; 2
4
7
3
5
6
3
6
3
5
7
1
4; 6
8
2
7
9
7
0
10
8
0
11
6
9
12
6
10
-
Сначала отобразим на диаграмме процесс 1 и 2. Оба процесса начинаются независимо друг от друга. Поэтому строим оба процесса с самого начала.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
2
-
процесс 3 длительностью 1 начинается только после окончания процессов 1 и 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
3
2
-
Процессы 4 и 5 начинаются после выполнения процесса 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
3
4
2
5
-
Процесс 6 начинается после выполнения процесса 5. Процесс 7 начинается после завершения процессов 4 и 6. Процесс 8 начинается после завершения процесса 7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
3
4
7
8
2
5
6
-
Процессы 9 и 10 начинаются сразу в момент 0, так как независимы от других процессов. Процесс 11 начинается после завершения процесса 9, а процесс 12 процесс сразу после завершения процесса 10.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
3
4
7
8
2
5
6
9
11
10
12
-
Позже всех – через 17 мс – заканчивается процесс 8. Это и есть минимальное время завершения всей совокупности процессов. -
Ответ: 17.