Порядок выполнения.

1. 
   Вывести выражение для вычисления значений в столбце «Принят, не принят». Для этого нужно составить Логическую конструкцию, в условии поставить адрес проходного балла. (рис. 54).
   

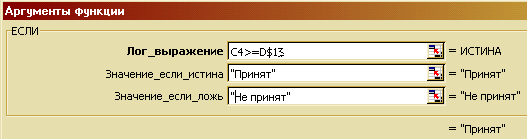
Рис. 54

При проходном балле 0 , естественно, все будут приняты.

2. 
   B ячейке D12 организовать подсчёт количества принятых с помощью функции СЧЁТЕСЛИ. Раз все приняты, то в ячейке D12 появится число 8.
   
3. 
   Выделить ячейку D13. Вызвать диалог «Подбор параметра». Данные - Работа с данными - Анализ "что-если" - Подбор параметра... Заполнить его как на рис. 55 , щёлкнуть ОК.
   

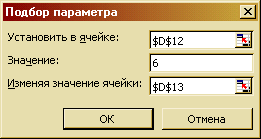
Рис. 55

В результате подсчета параметра значение проходного бала станет 35 и количество принятых станет равно плану приёма, (табл. 12 )

Таблица 12

№пп	Фамилия	Набрано баллов	Принят, не принят
1	Арбузова	50	Принят
2	Богогмолов	49	Принят
3	Высотчина	50	Принят
4	Ганохина	30	Не принят
5	Гиясова	97	Принят
6	Гончаренко	40	Принят
7	Грицай	35	Не принят
8	Дудина	20	Не принят
		Принято	6
		Проходной балл	35
		План приёма	6

---

---

Упражнение 8. «Корни кубического уравнения»

Задание. Известно, что кубическое уравнение y = aХ ³ + bX ² + cX + d в интервале [x₁ ; x₂] имеет три действительных корня. Найти корни уравнения методом подбора параметра.

ПО ВАРИАНТАМ

Вариант	a	b	c	d	[x1 ; x2 ]
1	0,5	3	-1	-3	[-7 ; 2]
2	0,5	2	-0,5	-3	[-4,5 ; 2]
3	0,5	2	-1	-5	[-5 ; 2]
4	0,4	2	-2	-5	[-7 ; 3]
5	0,4	2	-3	-6	[-7 ; 3]
6	-0,4	-1	3	6	[-4 ; 3]
7	-0,4	-2	3	6	[-7 ; 3]
8	0,4	1	-3	-6	[-4 ; 3]
9	-0,4	-2	2	5	[-7 ; 3]
10	-0,5	-2	1	5	[-5 ; 2]
11	-0,5	-3	1	3	[-7 ; 2]
12	-0,5	-2	0,5	3	[-4,5 ; 2]
13	-0,4	-1	3	6	[-4 ; 4]
14	0,5	2	-1	-5	[-6 ; 3]
15	-0,5	-2	1	5	[-6 ; 3]
16	-0,4	-2	3	6	[-7 ; 3]
17	0,4	1	-3	-6	[-4 ; 3]
18	-0,4	-2	2	5	[-7 ; 3]
19	-0,5	-2	1	5	[-5 ; 2]
20	-0,5	-3	1	3	[-7 ; 2]
21	0,5	2	-0,5	-3	[-4,5 ; 2]
22	0,5	2	-1	-5	[-5 ; 2]
23	0,4	2	-2	-5	[-7 ; 3]

---

Порядок выполнения для кубического уравнения У=0,5Х³+2X²-X-3 на участке от -5 до 2.

1. 
   Подготовить таблицу (табл.13) .
   

Таблица 13

	А	В	С
	Корни уравнения У=0,5Х3+2Х2-Х-3
		Левая часть (y)	Корни (x)
	1
	2
	3

2. 
   В ячейке В3 вывести формулу: =0,5*C3^3+2*C3^2-C3-3
   
3. 
   С помощью маркёра заполнения продолжить эту формулу на ячейки В5, В5.
   
4. 
   Так как в задании указана область поиска от -5 до 2, то расставим начальные значения корней -5,0 и 2, через 0. Тогда исходное состояние таблицы примет вид табл. 14.
   

Таблица 14

	А	В	С
	Корни уравнения У=0,5Х3+2Х2-Х-3
		Левая часть (y)	Корни (x)
	1	-10,5	-5
	2	-3	0
	3	7	2

---

5. 
   Установить курсор в ячейке В3, вызвать диалог «Подбор параметра», заполнить бланк как на рис. 56.
   

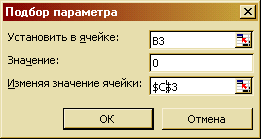
В результате выполнения этой операции в ячейке В3 появится число, записанное в экспоненциальной форме, близкое к нулю, а в ячейке значение первого корня -4,13264.

6. 
   Повторить подбор параметра для ячеек В4 и В5. В результате получится табл. 14.
   

Таблица 14

	Левая часть	Корни
1	-3,29599E-05	-4,1326416
2	-0,000197104	-1,1403808
3	0,000296781	1,2731184

---

Смотрите также файлы

• Текст песни Агата Кристи Как на войне.docx

• Опишите технологию проблемного обучения.docx

• Вопросы Понятие налоговой системы.pdf

• 1. Рассмотрите таблицу Методы биологических исследований. Запишите в ответе пропущенный термин, обозначенный в таблице вопросительным знаком.docx

• Физические и химические методы подготовки воды.docx