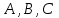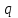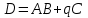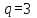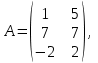
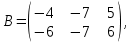
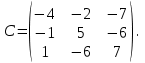
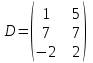
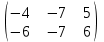
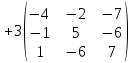
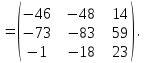
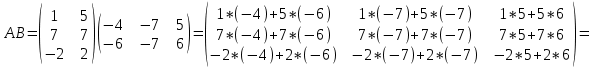
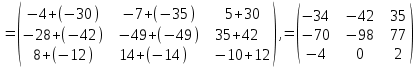
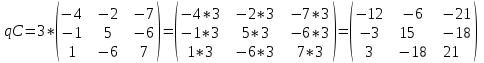
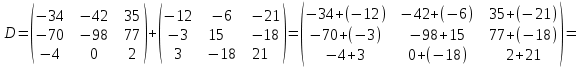
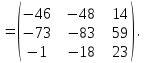
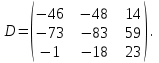
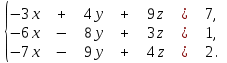
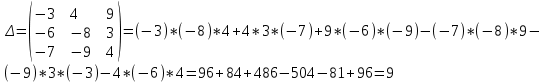
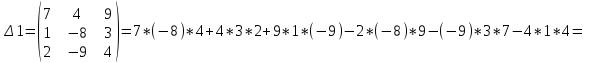
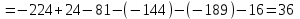
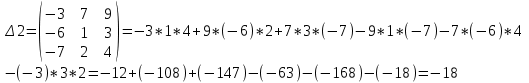
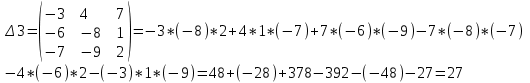
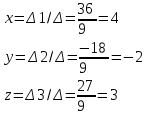
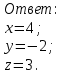
Кафедра математических и естественно-научных дисциплинРейтинговая работа: контрольная работапо дисциплине: математикаЗадание/вариант № 1Москва – 2021 г.1) Даны матрицы и число . Найти матрицу .1). , Ответ: 2) Дана система линейных алгебраических уравненийНайти решение этой системы любым методом.1). 3)

---

Известны координаты (см. таблицу 1) в прямоугольной системе координат 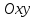трех точек 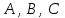, являющихся вершинами треугольника. Изобразить треугольник 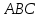в этой прямоугольной системе координат и найти: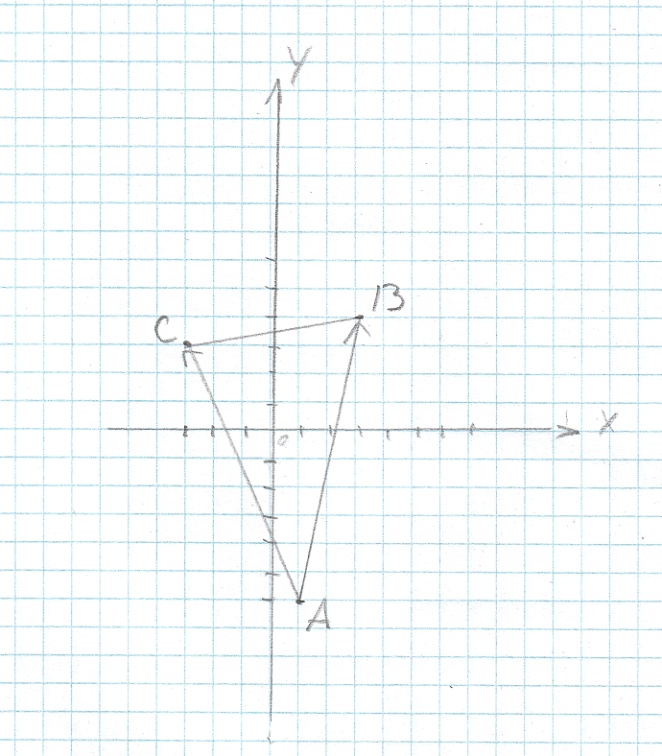



3.1 координаты векторов 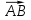, 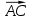и их длины;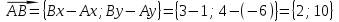







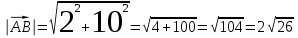
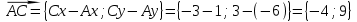
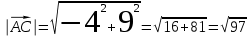
_Ответ:   <sub>;

;</sub>





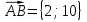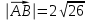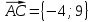
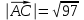
3.2 скалярное произведение векторов 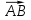, 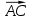и угол 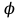между векторами , ;



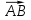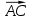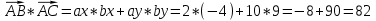
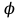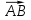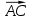Если взять формулу из лекции №2, то ab = |a||b| cos , где a = _; b= _{, а}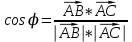

, тогда: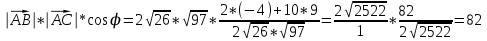







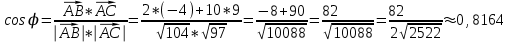
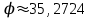
_{Ответ: скалярное произведение векторов равно 82; угол}

---

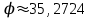
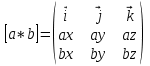
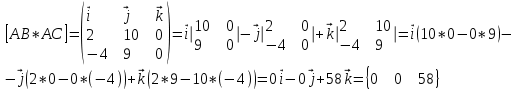
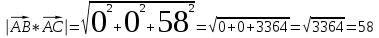
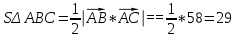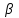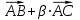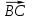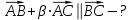
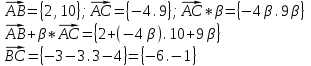
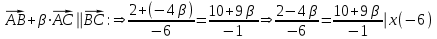
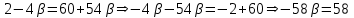
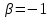
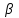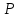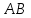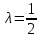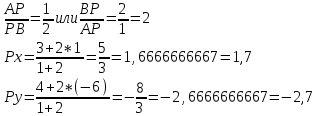
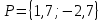
3.3 векторное произведение векторов , и площадь треугольника ;_{1) 2) (ед2)}Ответ: векторное произведение векторов , _{равно 58} и площадь треугольника _{равна 29 ед2.} 3.4 значение параметра , при котором векторы и будут коллинеарны;_{Ответ: значение параметра = -1, при котором векторы и будут коллинеарны.}3.5 координаты точки , делящей отрезок в отношении ;_Ответ: 3.6 каноническое уравнение стороны 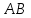;_{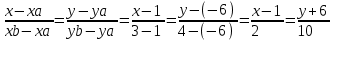Ответ:каноническое уравнение стороны} 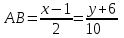3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку

---

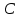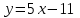
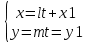
параллельно прямой ;Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:Составим параметрическое уравнение прямой. 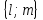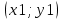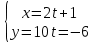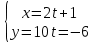Воспользуемся формулой параметрического уравнения прямой:где: - направляющий вектор прямой, в качестве которого можно взять вектор AB; - координаты точки лежащей на прямой, в качестве которых можно взять координаты точки A.В итоге получено параметрическое уравнение прямой:Ответ: параметрическое уравнение прямой:Таблица 1

Номер варианта	Координаты точек
1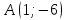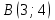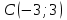
2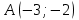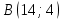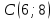
3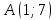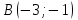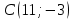
4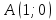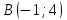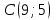
5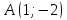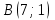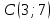
6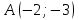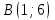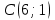
7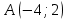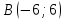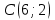
8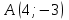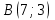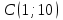
9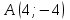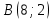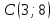
10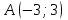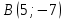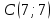

---

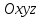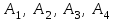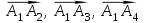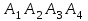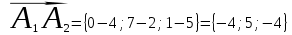
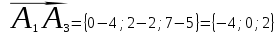
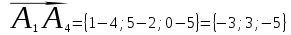
4) Известны координаты (см. таблицу 2) в прямоугольной системе координат вершин пирамиды .4.1найти смешанное произведение векторов и объем пирамиды ;1) Найдем вектор по координатам точек:2) Найдем смешанное произведение векторов: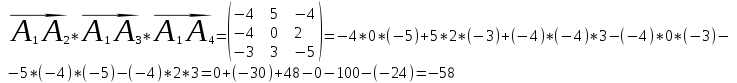_{3) Найдем обьем пирамиды А1А2А3А4: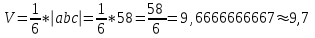Ответ: Смешанное произведение векторов равно: 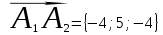; ;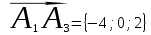 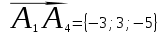и объем пирамиды А1А2А3А4 равен 9,7}4.2найти каноническое уравнение прямой 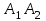;Воспользуемся формулой канонического уравнения прямой: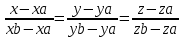Подставим в формулу координаты точек: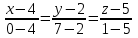В итоге получено каноническое уравнение прямой: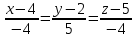Ответ: каноническое уравнение прямой 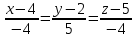4.3найти общее уравнение плоскости 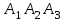;для составления уравнения плоскости используем формулу: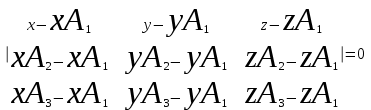Подставим данные и упростим выражение: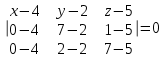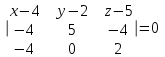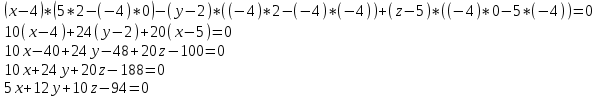Ответ: общее уравнение плоскости 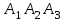_{:5x+12y+10z-94=0}

---

Смотрите также файлы

• Практическая работа к теме Доверие к государству Тема занятия Что мы Родиной зовём Класс 89.docx

• Разработка урока по геометрии Решение задач по теме.doc

• Организация неонатологической службы.pdf

• Глагольные счетные слова в китайском языке оглавление введение исследования понятия счетные слова.docx

• Физическое воспитание детей старшего школьного возраста.docx