ФГБОУ ВОУфимский государственный авиационный технический университетКафедра Математики

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
100
90
80
70
60
50
40
30
2
10
0

---

Пояснительная запискаК курсовой работеПо дисциплине «Дифференциальные уравнения»Решение задач Коши методами теории дифференциальных уравнений и операционного исчисления.

1502.Б1.О.111400.00 ПЗ

Группа ПМИ-254	Фамилия И.О.	Подпись	Дата	Оценка
Студент	Мова И.А.
Преподаватель	Мухаметова.Г.З
Принял	Байков В.А.

Уфа 2021ФГБОУ ВОУфимский государственный авиационный технический университетКафедра ИИиПМИЗАДАНИЕНа курсовую работу по дисциплине «Математический анализ»Студент Мова Ирина АлександровнаКонсультант Мухаметова Гульнара Зуфаровна1.Тема курсовой работыРешение задач Коши методами теории дифференциальных уравнений и операционного исчисления.2.Основное положениеРешить задачу Коши двумя способами, методом теории дифференциальных уравнений и методами операционного исчисления.

1. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’−3x’+ 2x =5, x (0) = 0, x’(0) = 0.
   
2. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+ 25x = cos(4t), x(0) =1, x’(0) = 0.
   
3. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+16x’ =sin(3t) x(0) = 0, x’(0) = 2.
   
4. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+5x’+ 4x =3, x(0) =3, x’(0) = 4.
   

Дата выдачи задания Дата окончания работы«____» __________ 2021г. «____» __________ 2021г.Руководитель работы __________Мухаметова Г.З.Содержание

---

1.Постановка задачи……………………………………………………………....42.Теоретическая часть…………………………………………………………….5 3.Практическая часть……………………………………………………………..9Заключение………………………………………………………………………18Список литературы………………………………………………………………191.Постановка задачиНайти решения задачи Коши двумя способами, методом теории дифференциальных уравнений и методами операционного исчисления.

1. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’−3x’+ 2x =5, x(0) = 0, x’(0) = 0.
   
2. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+ 25x = cos(4t), x(0) =1, x’(0) = 0.
   
3. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+16x’ =sin(3t) x(0) = 0, x’(0) = 2.
   
4. 
   Дано дифференциальное уравнение с заданными начальными условиями, x’’+5x’+ 4x =3, x(0) =3, x’(0) = 4.
   

ТеоретическаячастьОперационное исчислениеФункцией-оригиналом называется любая комплекснозначная функция f(t)Действительного аргумента t, удовлетворяющая условиям:

1. 
   f(t) интегрируема на любом конечном интервале оси t (локально интегрируема)
   
2. 
   Для всех t<0 : f(t)=0
   
3. 
   |f(t)| возрастает при t→+∞ не быстрее показательной функции,
   

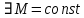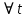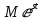
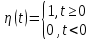
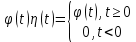
т.е. >0 и s>0: → | f(t)|≤S-нижняя грань всех чисел s, называется показателем роста функции f(t).Функции, удовлетворяющие этим трём требованиям, называются в операционном исчислении изображаемыми по Лапласу или оригиналами.Простейшим оригиналом является функция Хевисайда:Очевидно, чтогде 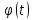удовлетворяет условиям 1˚ и 3˚, то 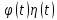удовлетворяет всем условиям, налагаемым на оригиналы.f(t)-оригиналИзображением по Лапласу функции f(t) называется функция комплексного переменного p=a+ib, определяемая равенством

---

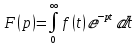
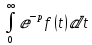
F(p) –изображение f(t) , обозначается L(f(t))=F(p).Функция F(p) определена на полуплоскости Re p=s>S и является в этой полуплоскости аналитической функцией.Свойства преобразования Лапласа1.Теорема единственностиПреобразование Лапласа F(p)=Две функции 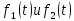, имеющие одинаковые преобразования Лапласа, совпадают во всех точках непрерывности для всех t>0

1. 
   Свойство линейности
   

Для любых комплексных постоянных u и vL(uf(t)+vg(t))=uF(p)+vG(p), где L(f(t))=F(p) и L(g(t))+G(p)

2. 
   Теорема подобия
   

Для любого c=const >0

3. 
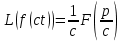
   Дифференцирование оригинала
   

Если функции 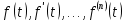являются оригиналами и …………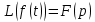

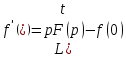
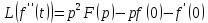
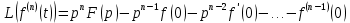
4. 
   Дифференцирование изображения
   

Дифференцирование изображения сводится к умножению на (-t) оригинала

5. 
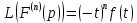
   Интегрирование оригинала
   

Интегрирование интеграла сводится к делению изображения на p 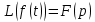, то

6. 
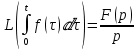
   Интегрирование изображения
   

Если интеграл 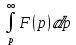сходится, то он служит изображением функции :

7. 
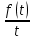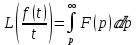
   Теорема смещения
   

Если L(f(t))=F(p), то для любого комплексного

8. 
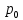
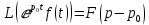
   Теорема запаздывания
   

Если L(f(t))=F(p), то для любого положительного T

---

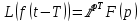
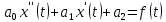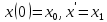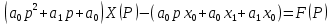
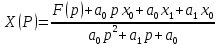
Пусть дано дифференциальное уравнение, где f(t) функция-оригинал (1)удовлетворяющее начальным условиям (2)Применим преобразование Лапласа к обоим частям уравнения, используя дифференцирование оригинала и свойство линейности преобразования Лапласа, и подставим начальное условие. Получим операторное уравнениеВыразив из него X(p) – операторное решение.Находя по X(p) оригинал x(t), получим решение задачи Коши (1)(2)

Оригинал	Изображение	Оригинал	Изображение
1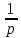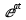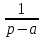

---

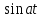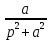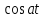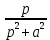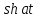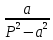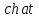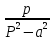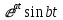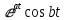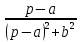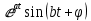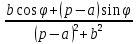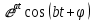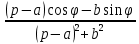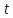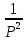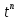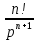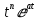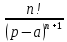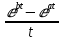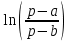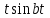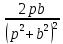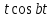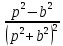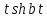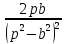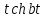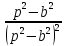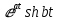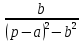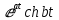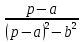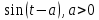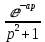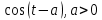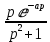Смотрите также файлы

• Дисциплина Документационное обеспечение логистических процессов Практическое задание 3, Модуль 3.doc

• Резюме для начинающих.pdf

• Информационные технологии в юридической деятельности.pdf

• .docx

• Практическая работа 1 Функциональная грамотность и функциональная безграмотность обучающихся как результаты школьного обучения.docx