Файл: Лекция д т. н., профессора Курейчика В. М. Генетические алгоритмы. Состояние. Проблемы. Перспективы.doc

Для решения многих оптимизационных задач можно использовать некоторые классы алгоритмов, называемых «жадными». Такой алгоритм делает на каждом шаге локально оптимальный выбор, - в надежде, что итоговое решение также окажется оптимальным. Это не всегда так – но для многих задач такие эвристические алгоритмы дают оптимальный результат. Говорят, что к оптимизационной задаче применим принцип «жадного» выбора, если последовательность локально-оптимальных («жадных») выборов дает оптимальное решение. «Жадный» оператор – это языковая конструкция, позволяющая создавать новые решения на основе частичного выбора на каждом шаге преобразования локально оптимального значения целевой функции.

Рассмотрим «жадный» оператор кроссинговера. Он может быть реализован на двух и более хромосомах, а в пределе на всей популяции. Приведем алгоритм «жадного» ОК на примере нахождения пути с минимальной или максимальной стоимости на графе:

1. Для всех хромосом популяции вычисляется ЦФ (стоимость пути между всеми вершинами графа). Выбирается заданное число родительских хромосом, и случайным образом на одной из хромосом определяется точка «жадного» ОК.

2. В выбранной хромосоме для i-го гена, расположенного слева от точки «жадного» ОК, определяется значение частичной ЦФ. Например, это стоимость пути от выбранного гена к ближайшему, находящемуся справа гену. Аналогичные действия выполняются по определению стоимости пути от i-го гена во всех остальных хромосомах, выбранных для «жадного» ОК.

3. В хромосому «потомок» выбирают тот ген, у которого значение ЦФ выше (ниже) при максимизации (минимизации) значения ЦФ.

4. Процесс продолжается аналогично, пока не будет построена хромосома «потомок». Если в процессе реализации «жадного» ОК возникает цикл или тупик, то в потомок выбираются нерассмотренные гены с лучшим значением ЦФ.

Например, пусть задан граф G = (X, U), X = {a, b, c, d, e}, в виде матрицы. Построим популяцию P, состоящую из трех родительских хромосом P={P₁,P₂,P₃}, где P₁ : (abcde); P₂ : (bdeca); P₃ : (ebadc). Элементы матрицы определяют стоимость пути между любыми двумя вершинами графа, а каждый гена в хромосоме кодируется номером вершины графа.



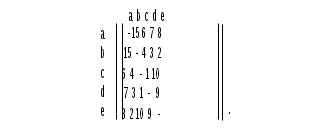
Согласно алгоритму выберем точку «жадного» ОК между генами b и c в хромосоме P

---

₁. Теперь выбор (b – c) дает значение ЦФ равное 4 (см. матрицу), выбор (b – d) (в хромосоме P₂) определяет ЦФ со значением 3, а выбор (b – a) (в хромосоме P₃) определяет ЦФ равную 15. При минимизации ЦФ выберем путь (b – d). Продолжая далее, получим путь реализации «жадного» ОК (рис. 2.1). Итак, хромосома потомка P': b d c a e имеет суммарную ЦФ равную 18 (3+1+6+8=18), а ЦФ родителей для P₁ равна 15+4+1+9=29, для P₂ равна 3+9+10+6=28 и для P₃ равна 2+15+7+1=25.



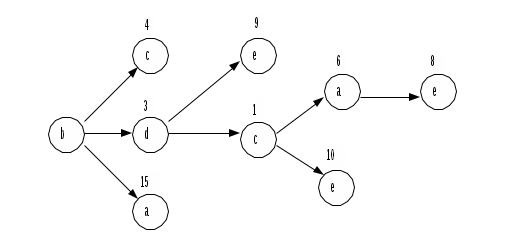
Пример реализации «жадного» ОК.

Стратегию «жадного» ОК можно выполнять различными способами. Следует отметить, что исследователи продолжают поиск универсальных ОК и специализированных ОК, ориентированных на решение заданного класса задач.

Рассмотрим различные варианты выбора пары хромосом для скрещивания. Вероятность скрещивания лучших хромосом с худшими (по значению ЦФ), должна уменьшаться при эволюции поколений.

Выбор первой хромосомы осуществляется с вероятностью



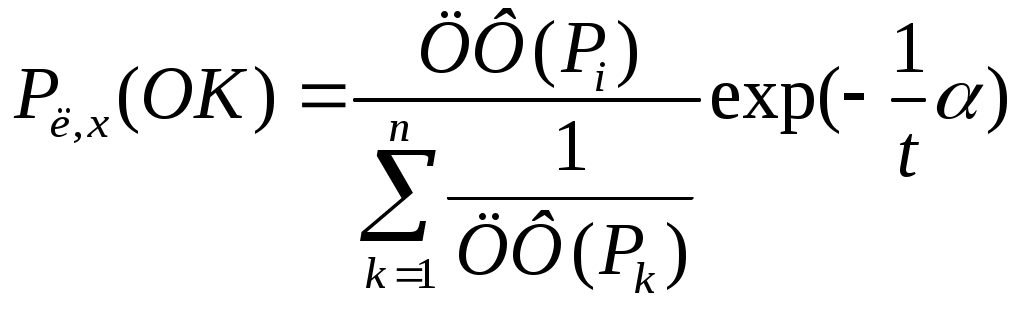
выбор второй хромосомы



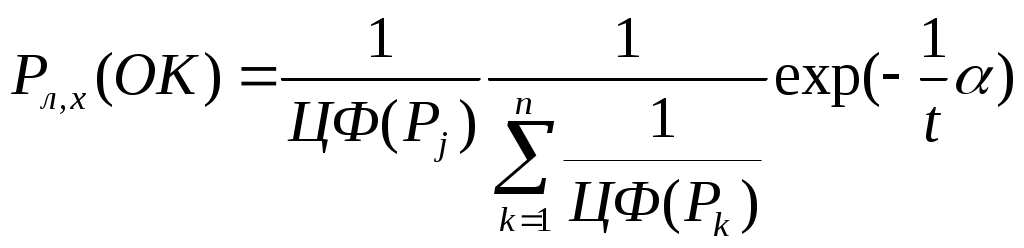
Вероятность скрещивания лучших хромосом должна увеличиваться на последних этапах оператора кроссинговера для закрепления желаемых признаков в хромосомах. Существуют и другие методы выбора пар хромосом для скрещивания. Например, «близкое» родство, «дальнее» родство, выбор на основе кода Грея и т.д.

«Близкое родство». Здесь вероятность выбора хромосом, подлежащих скрещиванию, запишется:

- Для первой хромосомы P_i



где - вероятность выбора первой хромосомы на основе близкого родства.

- Для второй хромосомы P_j вероятность вычисляется по формуле, но из оставшихся хромосом P \ {P_i}, где P – текущая популяция.

Затем вычисляется Хеммингово расстояние dist(Pi,Pj) между выбранными хромосомами текущей популяции.

---

Здесь Хеммингово расстояние равно количеству позиций с несовпадающими значениями генов в бинарных хромосомах.

Хромосомы рекомендуются для скрещивания, если Хеммингово расстояние между ними dist(Pi,Pj) > R, где R радиус скрещивания, задаваемый лицом принимающим решение или определяется как ближайшее меньшее целое от разности значений целевых функций: ЦФ(Pi) – ЦФ(Pj) деленное на два.

Вероятности и возрастают на конечных стадиях работы оператора кроссинговера.

«Дальнее» родство

,

где - вероятность выбора хромосом при «дальнем» родстве на начальных стадиях работы ГА, с учетом особенностей вычисляется для первой и второй хромосомы.

Хромосомы P_i и P_j подлежат скрещиванию, если Хеммингово расстояние между ними dist(Pi,Pj) > R. Вероятность и уменьшается на конечных стадиях поиска оптимального решения.

Код Грея для хромосом представленных в двоичном виде. Код Грея это двоичный код, последовательные значения которого отличаются только одним двоичным разрядом. Например:

0 – 0000

1 – 0001

2 – 0011

3 – 0010

4 – 0110

5 – 0111 и т.д.

Такое кодирование альтернативных решений позволяет решать вопросы «взбалтывания» популяции, и эффективно на начальных стадиях генетического алгоритма.

Как следует из биологии, некоторые процессы преобразования популяции происходят толчками. Основой таких процессов являются точковые мутации. В генетическом алгоритме мутация необходима потому, что предотвращают потерю генетического материала. Точковые мутации не изменяют размера и строения хромосом, а изменяют взаимное расположение генов в хромосоме.

Оператор мутации - это языковая конструкция, позволяющая на основе преобразования родительской хромосомы (или ее части) создавать хромосому потомка.

Оператор мутации обычно состоит из двух этапов:

1. В хромосоме A = (a₁, a₂, a₃,...,a_L-2, a_L-1, a_L) определяются случайным образом две позиции (например, a

---

₂ и a_L-1).

2. Гены, соответствующие выбранным позициям, переставляются, и формируется новая хромосома А= (a₁, a_L-1, a₃,...,a_L-2, a₂, a_L).

Рассмотрим кратко основные операторы мутации (ОМ). Простейшим ОМ является одноточечный. При его реализации случайно выбирают ген в родительской хромосоме и, обменивая его на рядом расположенный ген, получают хромосому потомка. Например:

Р₁ : 0 1 1 | 0 1 1

Р'₁ : 0 1 0 | 1 1 1

Здесь Р₁ – родительская хромосома, а Р'₁ – хромосома – потомок, после применения одноточечного оператора мутации.

При реализации двухточечного ОМ случайным или направленным образом выбираются две точки разреза. Затем производится перестановка генов между собой, расположенных справа от точек разреза. Например:

Р : A | B C D | E F

P' : A E С D B F

Здесь Р₁ – родительская хромосома, а Р'₁ – хромосома – потомок, после применения двухточечного оператора мутации.

Развитием двухточечного ОМ является многоточечный (или n-точечный) ОМ. В этом случае происходит последовательный обмен генов, расположенных правее точек разреза друг с другом в порядке их расположения. Ген, расположенный правее последней точки разреза переходит на место первого. Например:

Р : A | B C D | E F | G H

P' : A G C D B F E H.

Строительные блоки (СБ) – это тесно сплетенные между собой гены (части альтернативных решений) которые нежелательно изменять при выполнении генетических операторов. Из строительных блоков (как из кирпичиков при построении дома) можно создавать альтернативные оптимальные или квазиоптимальные решения.

В частном случае, когда строительные блоки, расположенные между точками разреза одинаковы, многоточечный ОМ выполняется следующим образом. При четном числе точек разреза меняются местами гены, расположенные справа и слева от выбранных точек.

Например:

Р : A B | C D | E F | G H | I J

P' : A C B E D G F I H J.

При нечетном числе точек потомок получается после обмена участками хромосом, расположенных между четными точками разреза.

Например:

Р : A B C | D E F | G H I | J

P' : A B C G H I D E F J.

Часто используют ОМ, основанные на знаниях о решаемой задаче. Реализация таких операторов заключается в перестановке местами любых выбранных генов в хромосоме, причем точка или точки мутации определяются не случайно, а направленно.

В позиционном операторе мутации две точки разреза выбираются случайно, а затем ген, соответствующий второй точке мутации, размещается в позицию перед геном, соответствующим первой точке. Например:

---

Р : A | B C D | E F

P' : A E B C D F.

Введем понятие оператора инверсии. Оператор инверсии - это языковая конструкция, позволяющая на основе инвертирования родительской хромосомы (или ее части) создавать хромосому потомка. При его реализации случайным образом определяется одна или несколько точек разреза (инверсии), внутри которых элементы инвертируются.

Генетический оператор инверсии состоит из следующих шагов:

1. Хромосома В = b₁,b₂,…,b_L выбирается случайным образом из текущей популяции.

2. Два числа y’₁ и у’₂ выбираются случайным образом из множества {0, 1, 2, …, L+1}, причем считается, что у₁=min{y’₁, у’₂} и у₂=max{y’₁, у’₂}.

3. Новая хромосома формируется из В путем инверсии сегмента, который лежит справа от позиции у₁ и слева от позиции y₂ в хромосоме В. Тогда, после применения оператора инверсии, получаем: В₁=( ). B_L

Для одноточечного оператора инверсии запишем:

Р₂ : A | B C D E F G H

P'₂ : A | H G F E D C B

Здесь Р₂ – родительская хромосома, а Р'₂ – хромосома – потомок, после применения оператора инверсии.

Например, для двухточечного оператора инверсии получим:

Р₁ : A B C | D E F | G H

P'₁ : A B C | F E D | G H

Здесь Р₁ – родительская хромосома, а Р'₁ – хромосома – потомок, после применения двухточечного оператора инверсии.

Часто применяется специальный оператор инверсии. В нем точки инверсии определяются с заданной вероятностью для каждой новой создаваемой хромосомы в популяции.

Рассмотрим оператор транслокации. Оператор транслокации - это языковая конструкция, позволяющая на основе скрещивания и инвертирования из пары родительских хромосом (или их частей) создавать две хромосомы потомков. Другими словами он представляет собой комбинацию операторов кроссинговера и инверсии. В процессе его реализации случайным образом производится один разрез в каждой хромосоме. При формировании потомка Р’₁ берется левая часть до разрыва из родителя Р₁ и инверсия правой части до разрыва из Р₂ .При создании Р’₂ берется левая часть Р₂ и инверсия правой части Р₁. Например:

Р₁ : A B | C D E F

P₂ : G К | H I J Q

____________________

P'₁ : A B Q J I H

P'₂ : G K F E DC.

Существуют большое число других видов оператора транслокации. Отметим, что до последнего времени оператор транслокации не применялся в ГА, а также при разработке интеллектуальной ИС и решении оптимизационных задач.

---