Файл: Лекция д т. н., профессора Курейчика В. М. Генетические алгоритмы. Состояние. Проблемы. Перспективы.doc

Рассмотрим пример Д. Гольдберга: необходимо найти значение максимума функции f(x)=x² на целочисленном интервале [0, 31]. Традиционными методами можно изменять значения переменной x, пока не получим максимальное значение f(x).

Для объяснения и реализации ПГА построим следующую таблицу:

Номер хромосом	Хромосома (двоичный код)	Десятичный код	Значение ЦФ	Значение ЦФ, в процентах
1	0 1 1 0 0	12	144	16.2
2	1 0 0 0 0	16	256	28.8
3	0 0 1 1 1	7	49	5.5
4	1 0 1 0 1	21	441	49.5

В столбце 2 табл. расположены 4 хромосомы (представленные в двоичном коде), сгенерированные случайным образом. Значение ЦФ для каждой хромосомы (столбец 4) определяется как квадрат значения десятичного кода двоичного числа, которое приведено для хромосом во втором столбце таблицы. Тогда суммарное значение ЦФ всех хромосом равно 890. Для селекции хромосом используется оператор репродукции на основе колеса рулетки. На рисунке поля колеса рулетки соответствуют значению ЦФ каждой хромосомы в процентах. В одной генерации колесо рулетки вращается, и после останова ее указатель определяет хромосому, выбранную для реализации следующего оператора. Очевидно, не всегда хромосома с большим значением ЦФ в результате ОР будет выбрана для дальнейших преобразований.

Будем считать, в рассматриваемом примере, для упрощения, что 16,2=16; 49,5 = 50; 5,5 = 5; 28,8 = 29.



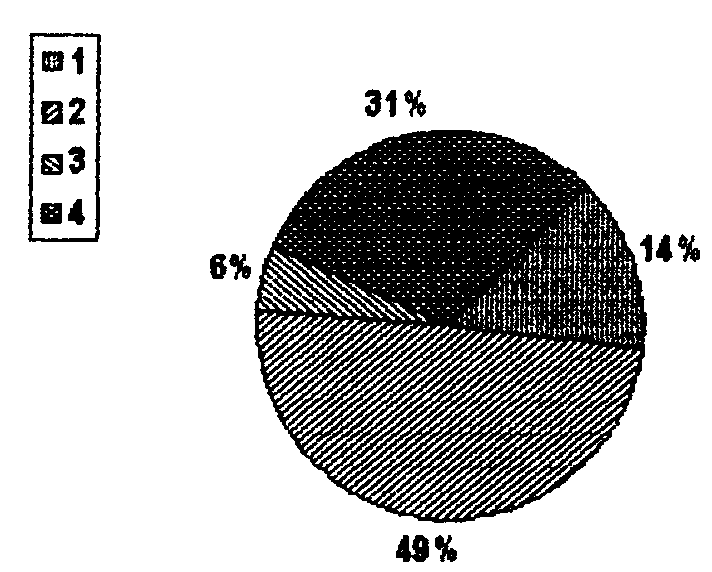
Колесо рулетки для примера

На основе реализации ОР выбираются хромосомы для применения ОК. Оператор кроссинговера, как правило, выполниться в 3 шага, одним из ОК описанным выше. Точка разрыва k выбирается случайно между 1 и числом равным длине хромосомы минус единица, то есть в интервале (1, L-1). Длина хромосомы L – это число значащих цифр в ее коде. В рассматриваемом примере таблицы длина каждой хромосомы равна пяти (L=5). На основе ОК создаются две новые хромосомы, путем обмена их частей между позициями (k+1) и L соответственно.

---

Например, рассмотрим хромосомы 1 и 2 из начальной популяции. Пусть k=1. Тогда получим:

P₁  0 | 1 1 0 0 До применения оператора кроссинговера

P₂  1 | 0 0 0 0,

-----------------

P₁  0 0 0 0 0 После применения оператора кроссинговера

P₂  1 1 1 0 0.

Работа ПГА начинается с репродукции. Хромосомы для следующей генерации выбираются путем вращения колеса рулетки. В примере колесо рулетки вращается 4 раза. Это число соответствуют мощности начальной популяции.

Величину отношения называют вероятностью выбора копий (хромосом) при реализации оператора репродукции и обозначают:






где f_i(x)  значение ЦФ i-й хромосомы в популяции, sum f(x)  суммарное значение ЦФ всех хромосом в популяции. Величину также называют нормализованной вероятностью выбора. Ожидаемое число копий

i-й хромосомы после реализации ОР определяются по формуле:



где  число анализируемых хромосом, причем N_G включается в N.

Ожидаемое число копий хромосомы P_i, переходящее в следующее поколение, также иногда определяют на основе выражения:

.

где  среднее значение ЦФ по всей популяции.

Тогда для рассматриваемого примера, ожидаемое число копий для первой хромосомы из таблицы равно 0,164=0,64 копий, для второй  0,294=1,16 копий, для третьей  0,054 = 0,2 и наконец для четвертой  0,54=2. Используя модель «бросание монеты» можно определить число полученных копий. Например, (см. столбец 7 таблицы) хромосомы P₁ и P₂ получают 1 копию, хромосома P₄– 2 копии, и хромосома 3 не получает копий. Сравнивая этот результат с ожидаемым числом копий, получаем то, что «лучшие» хромосомы дают большее число копий, «средние» остаются и «плохие» удаляются после реализации оператора репродукции.

№	Начальная популяция	x	f(x)	Значение fi(x)/sum[f(x)]	Ожидаемое число копий	Число полученных копий
1	0 1 1 0 0	12	144	0.16	0.65	1
2	1 0 0 0 0	16	256	0.29	1.15	1
3	0 0 1 1 1	7	49	0.05	0.22	0
4	1 0 1 0 1	21	441	0.5	1.98	2
Суммарное значение ЦФ (sumf(x))			890	1.00	4.00	4
Среднее значение ЦФ			222.5	0.22	0.88	1
Max значение ЦФ			441	0.5	2	2

---

Для рассматриваемого примера построим таблицу. В столбце 2 приведен вид 4 хромосом после выполнения оператора репродукции. В столбце 3 приведены списки пар хромосом, которые выбраны случайным образом для реализации оператора кроссинговера. В столбце 4 указан номер позиции для точки разреза хромосом. В столбце 5 приведен вид 4 хромосом после выполнения оператора кроссинговера. В столбце 6 приведены значения десятичного кода двоичного числа каждой хромосомы столбца 5. В столбце 7 приведено значение f(x) для каждой из 4 хромосом новой популяции. В строке 5 приведено суммарное значение ЦФ хромосом новой популяции, в строке 6 –среднее значение их ЦФ, а в строке 7- максимальное значение ЦФ хромосомы из новой популяции.

№	Популяция после оператора репродукции	Пары, выбранные случайно	Точка ОК	Новая популяция	x	f(x)
1	0 | 1 1 0 0	1-4	1	0 0 1 0 1	5	25
2	1 0 | 0 0 0	2-3	2	1 0 1 1 1	23	529
3	0 0 | 1 1 1	2-3	2	0 0 0 0 0	0	0
4	1 | 0 1 0 1	1-4	1	1 1 1 0 0	28	784
Sum f(x)	1338
	334.5
Max f(x)	784

Применяя к популяции полученной после реализации оператора репродукции (столбец 2 табл.) оператор кроссинговера, получим новую популяцию хромосом (5 столбец таблицы). В принципе оператор кроссинговера можно применять любое число раз. После проведения одной генерации ПГА улучшились все показатели: среднее и максимальное значение ЦФ.

Далее, согласно схеме выполнения ПГА, реализуется оператор мутации. Существует большое количество видов операторов мутации. Заметим, что эти операторы соответствуют перестановкам элементов внутри заданного множества. Очевидно, что при небольшой длине хромосомы L (порядка 1020) можно выполнить полный перебор за приемлемое время и найти наилучшие решения. При увеличении L до 50200 и выше, полный перебор произвести затруднительно, и необходимы другие механизмы поиска. Здесь как раз и приходит на помощь направленно-случайный поиск, который реализуется на основе ПГА.

---

Отметим, что глобальный максимум можно было найти еще на этапе реализации кроссинговера. Для этого необходимо было увеличить пространство поиска. Например, если в столбце 5 табл. выбрать хромосомы P₂ и P₄ и между ними выполнить оператор кроссинговера (точка ОК выбрана случайно и равна 3), то получим:

P₂: 1 0 1 | 1 1 (ЦФ-23)

P₄: 1 1 1 | 0 0 (ЦФ-28)

P 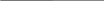₂: 1 0 1 0 0 (ЦФ-20)

P₄: 1 1 1 1 1 (ЦФ-31).

Решение P₄, полученное в результате применения ОК случайным образом, является наилучшим результатом (глобальным оптимумом).

Как отмечалось выше, в генетических алгоритмах можно выделять два основных механизма воспроизводства хромосом:

• 
  потомки являются точными копиями родителей (неполовое воспроизводство без мутации);
  
• 
  потомки имеют «большие» отличия от родителей.
  

В генетических алгоритмах в основном используют комбинации этих механизмов. Отметим, что в инженерных задачах начальная популяция может выбираться любым образом, например, моделированием «бросания монеты» (орел = 1, решка = 0). Тогда оператор репродукции выполняется через моделирование движения колеса рулетки. Оператор кроссинговера в задачах вычислительного характера обычно выполняется через двоичное декодирование двух положений монеты. Часто применяют другие типы ОК и другие технологии его выполнения. Вероятность ОК допускается равной Рr(ОК) = 1.0 и меньше, вероятность ОМ допускается равной Рr(ОМ) = 0.01 и больше. В общем случае вероятность применения оператора мутации зависит от знаний о решаемой задаче.

Приведем другой стандартный тип генетического алгоритма, описанный Л.Девисом:

1. 
   Инициализация популяции хромосом.
   
2. 
   Оценка значения каждой хромосомы в популяции.
   
3. 
   Создание новых хромосом посредством скрещивания текущих хромосом; применение операторов мутации и рекомбинации.
   
4. 
   Устранение хромосом из популяции, чтобы освободить место для новых хромосом.
   
5. 
   Оценка значений новых хромосом и вставка их в популяцию.
   
6. 
   Если время, заданное на реализацию алгоритма, закончено, то останов и возврат к наилучшей хромосоме, если нет, то переход к 3.
   
7. 
   Конец работы алгоритма.
   

Сравнивая описание ПГА Д. Гольдберга, Д. Холланда и Л. Девиса, видно, что в них реализована одна основная идея моделирования эволюции с некоторыми модификациями. Однако заметим, что эти изменения могут существенно влиять на окончательное качество решения.

---

Приведем пример модифицированного ПГА:

1. Создание начальной популяции решений.

2. Моделирование популяции (определение ЦФ для каждой хромосомы).

3. Пока не проведено необходимое число генераций или не закончилось время, заданное на реализацию алгоритма или не найдено оптимальное значение ЦФ (если оно известно):

а) выбор элементов для репродукции;

Применение:

б) оператора кроссинговера для создания потомков;

в) оператора мутации;

г) оператора инверсии;

д) оператора транспозиции;

е) оператора транслокации;

ж) оператора сегрегации;

з) оператора удаления вершин;

и) оператора вставки вершин;

к) рекомбинация родителей и потомков для создания новой генерации;

л) оператора редукции.

4. Реализация новой генерации.

Новые модификации ГА могут строиться путем объединения, например, пунктов «б – л» или их частичного устранения, или их перестановок, а также на основе применения адаптационных принципов управления эволюционным поиском.

Введение в аксиоматическую теорию генетических алгоритмов
Сформулируем описание генетических алгоритмов в виде научной теории. Отметим, что способ построения научной теории, в основе которой используются исходные положения, называемые аксиомами, а все остальные предложения теории получаются как логические следствия аксиом, называется аксиоматический метод. Аксиома - положение принимаемое без доказательств в качестве исходного, отправного для данной теории. Основным в нем является метод интерпретаций. Тогда для генетических алгоритмов можно построить следующую базовую теорию.

Пусть каждому исходному понятию и отношению аксиоматической теории ГА поставлен в соответствие некоторый конкретный математический объект. Совокупность таких объектов называется полем интерпретации. Всякому утверждению U теории ГА ставится в соответствие некоторое высказывание U* об элементах поля интерпретации, которое может быть истинным или ложным. Тогда можно сказать, что утверждение U теории ГА соответственно истинно или ложно в данной интерпретации. Поле интерпретации и его свойства сами обычно являются объектом рассмотрения другой теории ПГА, которая в частности может быть аксиоматической. Этот метод позволяет доказывать суждения типа: если теория ГА непротиворечива, то непротиворечива и теория ПГА.

---