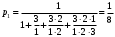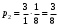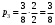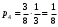1. 
   Дайте определение марковского процесса.
   

Пусть имеется некоторая система S, состояние которой ме­няется с течением вре­ме­ни (под системой S может по­ниматься тех­ни­ческое устройство, произ­вод­ст­венный процесс, вычислительная машина, информа­ци­онная сеть и т. д.). Если со­сто­яние системы S ме­ня­ется во времени случайным, заранее не­предсказуемым об­ра­зом, говорят, что в системе протекает слу­чайный процесс.Слу­чайный процесс, протекающий в системе S, называется марков­ским, или про­цессом без последействия, ес­ли он об­ла­да­ет следую­щим свойст­вом: для каж­дого момента времени t₀ вероят­ность любого состояния системы в будущем (при t> t₀) за­­­­ви­­сит то­лько от ее состоя­ния в настоящем (при t= t₀) и не зависит от того, когда и ка­ким об­разом система пришла в это со­стояние, т. е. как развивался про­цесс в прошлом.

2. 
   Как классифицируются марковские процессы?
   

Марковский случайный процесс (цепь Маркова) можно определить также как по­сле­довательность испытаний, в каждом из которых появляется только одно из k не­со­вместных событий A_i из полной группы. При этом условная вероятность p_ij(s) то­­го, что в s-ом испытании наступит со­бытие A_j при условии, что в (s – 1) – ом ис­пы­тании наступило событие A_i, не зависит от результатов пред­шествующих ис­пы­та­­ний. Независимые испытания являются частным случаем цепи Маркова. Со­бы­тия на­­­зываются состояниями системы, а испытания – изменениямисостоя­ний системы.Мар­ковские случайные процессы делятся на классы. Основными классифици­рую­­щи­ми признаками служат:

• 
  множество состояний, в которых может находиться система, и
  
• 
  моменты времени, в которые происходит изменение состояния системы.
  

3. 
   Что такое граф состояний и переходов Марковской цепи? Какие бы­вают ГСП?
   

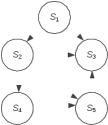
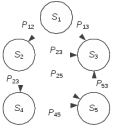
Анализ случайных процессов с дискретными состоя­ниями обычно проводится с по­мо­щью гра­фа состояний и пе­ре­ходов (ГСП).

---

Пусть имеется система Sс n дискретными состояниями:S₁, S₂, S₃, …, S_nКаждое состояние изображается окружностью, а воз­можные переходы (“пе­ре­ско­­ки”) из состояния в состо­я­ние – стрелками, соединя­ю­щими эти окружности. Удобно также по­ль­зо­ваться размеченным гра­фом, который графически изо­бра­­жает не то­лько во­з­мож­ные состояния си­сте­мы и воз­можные переходы из со­сто­я­ния в состо­я­ние, но также и значения вероятностей перехода. Примеры ГСП показаны на рисунке.

а)	б)

4. 
   Что понимается под матрицей переходных вероятностей?
   

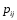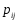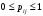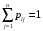Гра­фу системы, содержащему n вершин, можно поставить в соответствие ма­три­цу n×n, элементами которой яв­ля­ют­ся вероятности переходов между вер­ши­­нами графа, называемую матрицей вероятностей переходов. Элементы матри­цы удо­­в­лет­во­ряют условиям: (1) (2)Условие (1) – обычное свойство ве­роятностей, а условие (2) означает, что си­­с­те­ма S обязательно либо переходит из ка­кого-то состояния S_i в другое со­стояние, ли­бо остается в состоянии S_i. Эле­менты p_ijматрицы P обозначают вероят­но­сти пе­ре­хо­дов в системе за один шаг. Обычно на графе вероятности перехода системы из одного состояния в то же самое не отмечаются. При рассмотре­нии ко­н­­кре­т­ных систем удобно сначала построить граф со­стояний, затем оп­ре­делить вероятность переходов системы из одного со­­сто­я­­ния в то же самое (исходя из тре­бо­ва­ния равенства единице суммы элементов строк ма­трицы), а потом составить ма­трицу пе­ре­хо­дов системы.

5. 
   Как можно найти вероятность нахождения процесса в определенном со­сто­янии после определенного числа шагов?
   

---

при   в системе S устанавливается некоторый предельный стационарный режим: хотя система случайным образом и меняет свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Это свойство позволяет обходиться при нахождении параметров системы на основе моделирования одной достаточно длинной реализацией.Для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова, которые в случае нахождения предельных вероятностей превращаются в систему линейных алгебраических уравнений (уравнений глобального баланса) для каждого состояния.

6. 
   Что такое нестационарная марковская цепь?
   

Процесс o(t) предполагается нестационарной марковской цепью, начальное состояние которой га(0) = сцз считается известным. Множество состояний процесса конечно. Оно может формироваться для каждого t — 1,..., Т экспертом или программой с учетом известных взаимосвязей между макроэкономическими показателям. Если значения переходных вероятностей не зависят от номера шага, то мар­ков­­с­кая цепь называется однородной, илистаци­о­нарной

7. 
   Дайте определение марковского процесса с непрерывным временем и диск­ретными состояниями.
   

На практике встречаются ситуации, когда переходы системы из состояния в состо­я­ние происходят не в фикси­ро­ванные, а в слу­чайные мо­ме­нты времени, ко­то­рые за­ра­нее указать невоз­можно – переход может осуществиться в любой мо­мент. Нап­ри­­­мер, выход из строя (отказ) лю­бого элемента аппаратуры может про­и­зой­ти в лю­бой момент времени; окончание ремонта (вос­становление) этого элемен­та также мо­­жет произойти в заранее неизвестный момент и т. д.

---

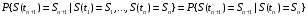
Для описания таких процессов может быть применена схема марковского слу­чай­но­го процесса с дискретными со­сто­я­ни­я­ми и непрерыв­ным временем. Такого типа про­­цессы известны как непрерывные цепи Маркова. Непре­рыв­ной цепьюМар­кова (мар­ков­ским процессом) называют процесс, для которого при 0≤ t₁≤ t₂≤…≤t_n+1 выполняется:Здесь так же, как и в случае процесса с дискретным временем, рассмат­ри­ва­ет­ся ряд дискретных состоя­ний: S₁,S₂, S₃, ..., S_n, од­на­ко переход системы Sиз со­стояния в состояние может происходить в произвольный мо­мент времени.

8. 
   Что такое предельные вероятности марковского процесса? Каков физи­чес­кий смысл предельных вероятностей?
   

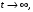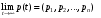
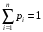
Весьма важным является вопрос о поведении функцийр₁(t), р₂(t), ..., р_n(t) при а именно, бу­дут ли они стремиться к каким-то пределам. Если пределы су­щ­е­ст­ву­ют, то они на­зы­ва­ют­ся предельными(финальными) вероятностями состояний: Очевидно, предельные вероятности состояний в сумме долж­ны давать единицу: Доказано, что если число состояний системы Sконечно и из каждого со­сто­я­ния мо­ж­но перейти за некоторое число ша­гов в любое другое, то предельные ве­ро­ят­но­сти состояний существуют и не зависят от на­чаль­но­го состояния системы.Таким образом, при 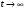в системе Sустанавливается неко­торый предельный ста­ци­онарный режим: хотя си­с­те­ма слу­чай­­ным образом и меняет свои состояния, но ве­роятность каждого из них не зависит от времени и ка­ждое из состояний осу­­­ще­ст­в­­ляется с некоторой постоян­ной вероятностью, которая представ­ляет собой сре­д­нее отно­си­тельное времяпре­бы­вания системы в данном состоянии. Это свой­ство по­з­воляет обходиться при нахождении параметров системы на основе моде­ли­­ро­ва­ния од­ной достаточно длинной реализацией.

---

Для ве­роятностей p₁(t), p₂(t),…, p_n(t)мо­жно составить систему линейных диф­фе­ре­н­­циальных ура­в­не­ний, назы­ва­емых урав­не­ни­ями Кол­мо­горова, которые в слу­чае на­хождения предельных вероятностей превра­щаются в систему ли­ней­ных ал­ге­браических урав­не­ний (уравнений глобального баланса) для каждого со­сто­я­ния. Со­в­местно с нор­ми­­ро­воч­ным условием эти уравнения да­ют воз­мож­ность вы­чи­слить все пре­де­ль­ные вероятности.

9. 
   Как найти предельные вероятности системы, имеющей стационарный режим?
   

стационарное распределение вероятностей

10. 
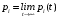
    Что называется процессом гибели и размножения? Поясните на ГСП.
    

Техническое устройство состоит из трех одина­ковых узлов, каждый из которых мо­­жет выходить из строя (отказы­вать). Отказавший узел не­ме­д­ле­нно начинает восстанавливаться. 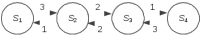Требуется найти вероятности числа от­казавших узлов.Состояния системы:S₁ – все три узла исправны:S₂– один узел отказал (восстанавливается), два исправны;S ₃– два узла восстанавливаются, один исправен;S ₄– все три узла восстанавливаются.ГСП имеет вид: Из графа видно, что процесс, протекающий в системе, пред­ст­а­в­ляет собой про­цесс размноже­ния и гибели.

11. 
    Запишите выражения для предельных вероятностей процесса гибели и размножения.
    

По предыдущему графу получаем:

---

Смотрите также файлы

• Влияние ценовой политики государства на финансовое состояние компаний.rtf

• Дисциплина Психофизиология Практическое задание 1, Модуль 1.docx

• Классификация зданий и сооружений.docx

• московский международный университет Кафедра юриспруденции Форма обучения заочная.docx

• Чемпионат по окружающему миру Подснежники2023. 12й класс.pdf