ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ

Кафедра информатики и компьютерных технологий

ЛАБОРАТОРНАЯ РАБОТА № 5

Вариант 9

Решение нелинейных уравнений средствами MathCAD

Выполнил: студент гр. ИЗБ-22-2 Талигин Г.Я.

^{(шифр группы) (подпись) (Ф.И.О.)}

Дата: 12.03.2023 г.

Проверил

руководитель практики: доцент Иванов В.Ю.

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург 2023

Задание 1. Постройте в MathCAD график нелинейной функции на заданном отрезке [a,b] согласно варианту. Найдите корень нелинейного уравнения на заданном отрезке тремя способами.



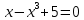
при заданных значениях a=1; b=2

Решение:

Результаты вычисления в программе Mathcad по условиям задачи номер один показаны на рисунках (см. Рисунок 1 и Рисунок 2)



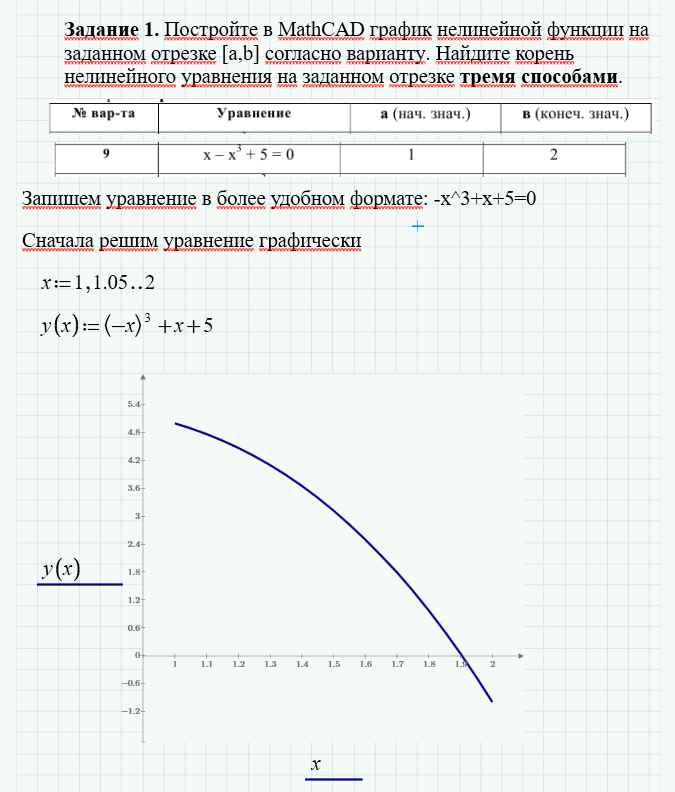
Рис. 1. Результаты вычисления по задаче №1



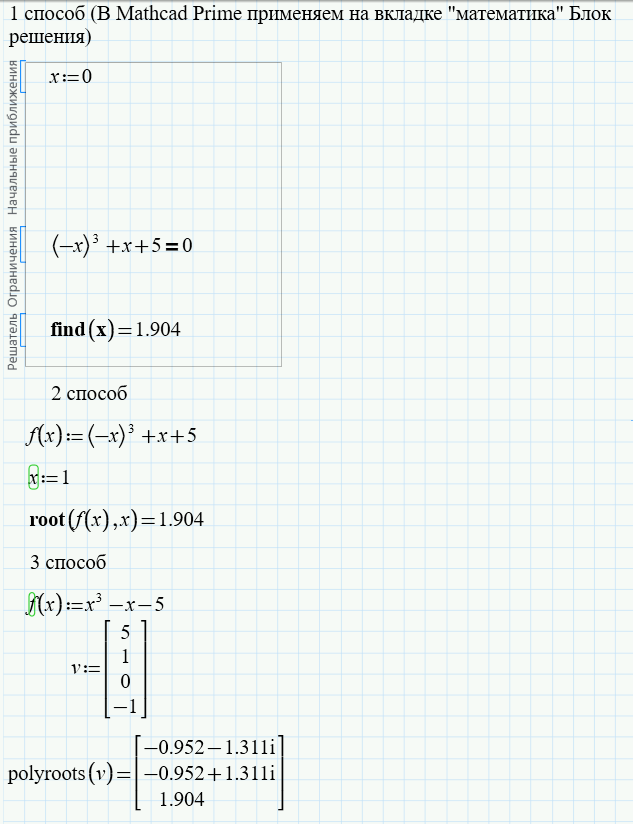
Рис. 2. Результаты вычисления по задаче №1

Задание 2. Найти корни трансцендентного уравнения f(x) = 0 (график + 2 способа решения).



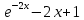
Решение:

Результаты вычисления в программе Mathcad по условиям задачи номер два показаны на рисунках (см. Рисунок 3 и Рисунок 4)



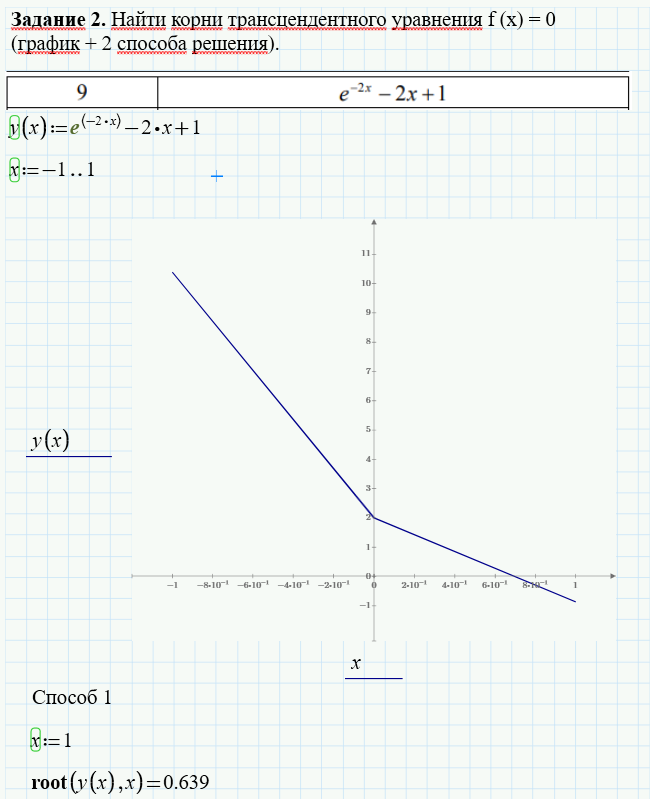
Рис. 3. Результаты вычисления по задаче №2

---

Рис. 4. Результаты вычисления по задаче №2

Задание 3. Решить систему уравнений:



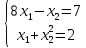
Решение:

Результаты вычисления в программе Mathcad по условиям задачи номер три показаны на рисунках (см. Рисунок 5, 6)



Рис. 5. Результаты вычисления по задаче №3



Рис. 6. Результаты вычисления по задаче №3

Задание 4. Вычислить определенный интеграл



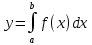
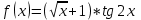
при заданных значениях a=0,6; b=0,72

Решение:

Результаты вычисления в программе Mathcad по условиям задачи номер четыре показаны на рисунке (см. Рисунок 7)



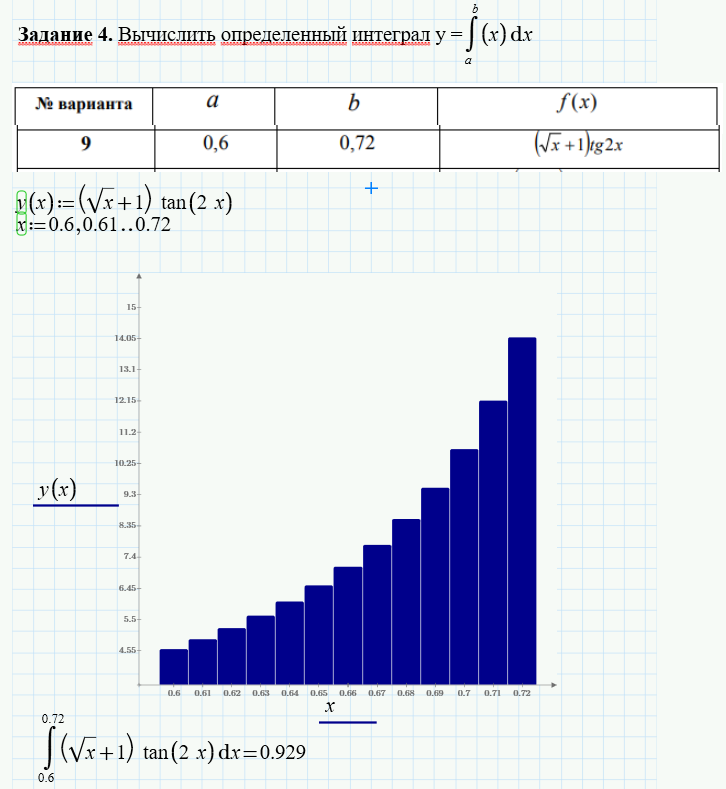
Рис. 7. Результаты вычисления по задаче №4

---

Смотрите также файлы

• Общая Характеристика Водорослей. Многообразие водорослей.pptx

• Практическая работа 4 Анализ открытого урока.doc

• Темы Курсовых работ по предмету Методы и средства проектирования информационных систем и технологи.docx

• Содержание Введение Цель функционирования предприятия Производственные и рыночные связи предприятия Формы предпринимательства Конкуренция и предприятие Заключение Перечень ссылок Введение.doc

• Задание Терминологический словарь Данное задание является пополняемым. На протяжении изучения курса Вам предстоит пополнять его наиболее актуальными терминами, определениями и аббревиатурами.docx