Файл: Повторение. Многочлен. Формулы сокращенного умножения..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 30
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Урок № 1
Тема: «Повторение. Многочлен. Формулы сокращенного умножения.»
8а
Тип урока: обобщение и систематизация знаний обучающихся
Цель урока: повторение и систематизация базовых знаний обучающихся, полученных в 7 классе по теме «формулы сокращенного умножения. Многочлен».
Задачи:
-
Отработать навык применения формул сокращенного умножения при решении заданий различного уровня сложности. -
формировать умение анализировать и обобщать знания по теме, развивать навыки устного счёта. -
воспитывать способности к самоанализу, трудолюбие, взаимопомощь.
Планируемые результаты:
Предметные: применяют формулы сокращенного умножения при выполнении заданий различного уровня сложности.
Личностные: Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к предмету.
Метапредметные:
Р – корректируют деятельность: вносят изменения в процесс с учетом возникших трудностей и ошибок, намечают способы их устранения.
П – делают предположения об информации, которая нужна для решения учебной задачи.
К – уважительно относятся к позиции другого.
Оборудование: мультимедийный проектор, компьютер, интерактивная доска, карточки
Методы обучения: фронтальный опрос, практическая тренировка, беседа, частично поисковый.
Структура урока:
| 1. | Организационный момент | 3 мин |
| 2. | Повторение опорного теоретического материала через устный счет | 5 мин |
| 3. | Формулирование темы и цели урока | 2 мин |
| 4. | Обобщение и систематизация понятий, усвоение системы знаний и их применение при выполнении практических заданий | 11 мин |
| 5. | Физкультминутка | 2 мин |
| 6. | Перенос приобретенных знаний и их первичное применение в новых условиях с целью формирования умений | 13 мин |
| 7. | Рефлексия | 2 мин |
| 8. | Постановка Д/З | 2 мин |
Ход урока
| Учитель | Ученики | УУД | ||||
| | |||||
| Приветствую учащихся. Сажаю их на места. Что необходимо иметь на уроке:
Знакомимся с учебником. | Приветствуют учителя. | К: следовать правилам поведения | ||||
| | |||||
| Эпиграфом нашего урока сегодня будут следующие слова: “Единственный путь, ведущий к знанию – это деятельность” Бернард Шоу. (слайд 1)
2ab; 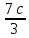 ; –3a²b; 7c; ; –3a²b; 7c; 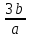 ;9ca²ca; 2ab + 7c; 5a²b ;9ca²ca; 2ab + 7c; 5a²b
- Что такое многочлен? - Какой многочлен называется многочленом стандартного вида? (слайд 2) Представьте многочлен в стандартном виде, где это необходимо 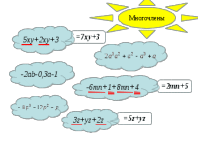 - Что называется степенью многочлена? (слайд 3) 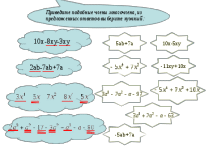 определите степень полученного многочлена. (слайд 4) Блицопрос:
Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второго плюс квадрат второго. (a+b)2=a2+2ab+b2
Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второго плюс квадрат второго. (a-b)2=a2-2ab+b2
Произведение суммы двух величин на их разность равно разности их квадратов. (a+b)(a-b)=a2-b2
Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второго плюс утроенное произведение первого на квадрат второго плюс куб второго. (a+b)3=a3+3a2b+3ab2+b3
Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второго плюс утроенное произведение первого на квадрат второго минус куб второго. (a-b)3=a3-3a2b+3ab2-b3
Произведение суммы двух выражений на неполный квадрат разности равно сумме их кубов. ( a+b)(a2-ab+b2)=a3+b3
Произведение разности двух величин на неполный квадрат суммы равно разности их кубов. (a-b)(a2+ab+b2)=a3- b3
Преобразуйте выражение в многочлен стандартного вида а) a2+(3a-b) 2 б) (3a-b)(3a+b)+b2 в) (5c+7d) 2-70cd г) x3+(2-x)(x2+2x+4) - Какие знания необходимы для выполнения данного задания? | отвечают с места по одному - если каждый его член представлен в стандартном виде и нет подобных слагаемых. Степенью ненулевого многочлена называетсянаибольшая из степеней одночленов, входящих в этот многочлен. Выполняют самостоятельно с последующей взаимопроверкой Отвечающий записывает формулу на доске. Устно выполняем задание применив формулы сокращенного умножения Формул сокращенного умножения | П: уметь ориентироваться в своей системе знаний К: уметь слушать и понимать речь других, оформлять мысли в устной речи Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение | ||||
| ||||||
Сегодня на уроке я хочу:
| Слушают. Записывают. отвечают | | ||||
| ||||||
| (слайд 8) Преобразуйте выражение в многочлен стандартного вида а) a2+(3a-b) 2 б) (3a-b)(3a+b)+b2 в) (5c+7d) 2-70cd г) x3+(2-x)(x2+2x+4) Проверка а) a2+(3a-b) 2=a2+9a2+b2-6ab=10a2+b2-6ab б) (3a-b)(3a+b)+b2=9a2-b2+b2=9a2 в) (5c+7d) 2-70cd=25c2+49d2+70cd-70cd=25c2+49d2 г) x3+(2-x)(x2+2x+4)=x3+23-x3=8 Задание 3 (слайд 9) Решите уравнение: а)(x-6) 2-x(x+8)=2 б)x(x-1)-(x-5) 2=2 Проверка:
Ответ: 1,7 Ответ: 3 Кто справляется с заданием успешно – дополнительно на карточке: Докажите, что выражение(5m-2)(5m+2)-(5m-4) 2- 40m не зависит от значения переменной. Ответ: (5m-2)(5m+2)-(5m-4) 2-40m=25m-24-(25m2+16-40m)-40m=25m2-4-25m2-16+40m-40m=-20 | Один ученик а, другой б, третий в, четвертый г. у доски, остальные в тетрадях Выполняют два ученика одновременно у доски, остальные в тетрадях. | П: уметь добывать новые знания (находить ответы на вопросы используя учебник, свой жизненный опыт и информацию полученную на уроке) | ||||
| ||||||
| За партой: разминаем руки + логические задачи Задача 1: (слайд 10) На решение этой задачи у шестилетнего ребенка уходит обычно не больше 20 секунд. А вот неподготовленных взрослых она часто вводит в ступор. Так какое же число скрыто под машиной? 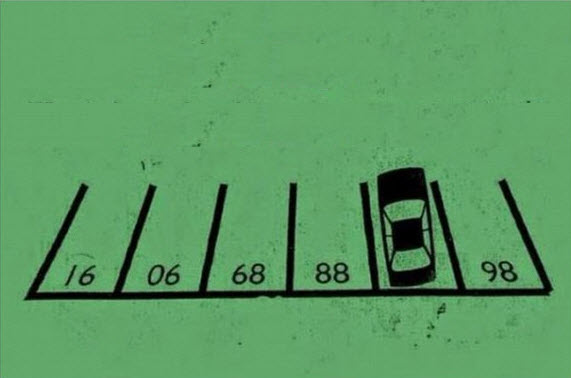 В действительности же, картинку надо просто перевернуть. Ответ: 87 | Выполняют | | ||||
| ||||||
| Задание 4. (слайд 11) Найди значение выражения: (6a−8b)⋅(6a+8b) − 36a2, если a=2 и b=0,01 Задание 5 (слайд 12) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 37 больше произведения двух других чисел. Решение: Пусть первое число х, тогда второе – (х + 1), а третье – (х + 2). Зная, что (x+2) 2 больше x(x+1) на 37, составим и решим уравнение: (x+2) 2 - x(x+1)=37 x=11 11- 1 число, 12- 2 число, 13- 3 число. Ответ: 11, 12, 13. Задание 6 из ОГЭ (слайд 13) Задание 6 № 338494 Решите уравнение Решение. Последовательно получаем: Ответ: −9,7. Дополнительно: Задание 21 № 311591 Решите уравнение: Решение. Перенесем все члены влево и применим формулу разности квадратов: Другой способ. Раскроем скобки, пользуясь формулой квадрата разности: Ответ: 1. Задание 7 (слайд 14) (если останется время) Упростите выражение: а) в) Решение: а) 3d-3+d2-d-d2+4d-4=6d-7 б) 5x2+10xy+5y2-10xy=5x2+5y2 в) z3+27-z3=27 (слайд 15) Найдите значение выражения ab – bc – ac, если a2+b2+c2=19 и a+b-c=7. Решение: а + b - c = 7 ((а + b) – c)2 = 72 (a + b)² - 2(a + b)·c + c² = 49 a² + 2ab + b² - 2ac - 2bc + c² = 49 a² + b² + c² + 2(ab - ac - bc) = 49 19 + 2(ab - ac - bc) = 49 2(ab - ac - bc) = 49 - 19 2 (ab - ac - bc)= 30 ab - ac - bc= 15 Ответ: 15 | Один ученик у доски остальные в тетрадях 36а2-64b2+36a2= -64b2 64*(0,01)2 =64*0,0001 =0,0064 Один ученик у доски остальные в тетрадях Один ученик у доски остальные в тетрадях Один ученик у доски остальные в тетрадях Один ученик у доски остальные в тетрадях | П: делают предположения об информации, которая нужна для решения учебной задачи. К: умеют критично относиться к своему мнению Р: понимают причины своего неуспеха и находят пути выхода из него. | ||||
| 7. Рефлексия | | |||||
| Отвечают с места | | ||||
| 8. Постановка Д/З | | |||||
| Карточка с д/з | записывают. | | ||||
Карточка:
| Докажите, что выражение (5m-2)(5m+2)-(5m-4) 2-40m не зависит от значения переменной. | Докажите, что выражение (5m-2)(5m+2)-(5m-4) 2-40m не зависит от значения переменной. |
а) 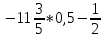 б) 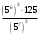 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
а) 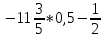 б) 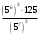 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
а) 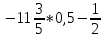 б) 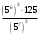 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
а) 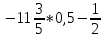 б) 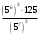 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
а) 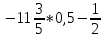 б) 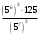 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
а) 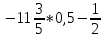 б) 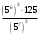 . .2. Решить уравнения: а) (2х+3)2 – 4(х-1)(х+1) = 49 б) (х + 2)(х2 – 2х + 4) = 7 3. Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. 4. Упростите выражение: 4у(у - 4) - (у – 8)2. 5. Найдите значение выражения a2+b2+c2, если a - b + c =8 и ac – bc – ab =12. |
| | |
| Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. | Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. |
| Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. | Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. |
| Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. | Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. |
| Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. | Домашнее задание: 1) Найдите значения выражения 2) Решить уравнение. 3) Решите задачу: Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 19 больше произведения двух других чисел. |
| Карточка 1 1. Упростите выражение: а) 3(а-2) = б) (а+1)(4+3а) = в) 2а2 (3-2а+4а2) = 2. Вынесите общий множитель за скобки: а) 5х+4х2 = в) (х+5)2у-7(х+5) = г) 3(а-4)+5с(4-а)= | Карточка 2 1. Найдите произведение многочленов: а) (3х – 2у) (3х + 2у); б) (4 + х2) (х2 – х). 2. Вынесите общий множитель за скобки: а) 3х-9 = б) 2х+7х2 = в) (х+2)2у-7(х+2) = г) 4(а-7)+9а(а-7) = д) 3(а-4)+5с(4-а)= |
| Карточка 1 1. Упростите выражение: а) 3(а-2) = б) (а+1)(4+3а) = в) 2а2 (3-2а+4а2) = 2. Вынесите общий множитель за скобки: а) 5х+4х2 = в) (х+5)2у-7(х+5) = г) 3(а-4)+5с(4-а)= | Карточка 2 1. Найдите произведение многочленов: а) (3х – 2у) (3х + 2у); б) (4 + х2) (х2 – х). 2. Вынесите общий множитель за скобки: а) 3х-9 = б) 2х+7х2 = в) (х+2)2у-7(х+2) = г) 4(а-7)+9а(а-7) = д) 3(а-4)+5с(4-а)= |
| Карточка 1 1. Упростите выражение: а) 3(а-2) = б) (а+1)(4+3а) = в) 2а2 (3-2а+4а2) = 2. Вынесите общий множитель за скобки: а) 5х+4х2 = в) (х+5)2у-7(х+5) = г) 3(а-4)+5с(4-а)= | Карточка 2 1. Найдите произведение многочленов: а) (3х – 2у) (3х + 2у); б) (4 + х2) (х2 – х). 2. Вынесите общий множитель за скобки: а) 3х-9 = б) 2х+7х2 = в) (х+2)2у-7(х+2) = г) 4(а-7)+9а(а-7) = д) 3(а-4)+5с(4-а)= |
| Карточка 1 1. Упростите выражение: а) 3(а-2) = б) (а+1)(4+3а) = в) 2а2 (3-2а+4а2) = 2. Вынесите общий множитель за скобки: а) 5х+4х2 = в) (х+5)2у-7(х+5) = г) 3(а-4)+5с(4-а)= | Карточка 2 1. Найдите произведение многочленов: а) (3х – 2у) (3х + 2у); б) (4 + х2) (х2 – х). 2. Вынесите общий множитель за скобки: а) 3х-9 = б) 2х+7х2 = в) (х+2)2у-7(х+2) = г) 4(а-7)+9а(а-7) = д) 3(а-4)+5с(4-а)= |
| Карточка 1 1. Упростите выражение: а) 3(а-2) = б) (а+1)(4+3а) = в) 2а2 (3-2а+4а2) = 2. Вынесите общий множитель за скобки: а) 5х+4х2 = в) (х+5)2у-7(х+5) = г) 3(а-4)+5с(4-а)= | Карточка 2 1. Найдите произведение многочленов: а) (3х – 2у) (3х + 2у); б) (4 + х2) (х2 – х). 2. Вынесите общий множитель за скобки: а) 3х-9 = б) 2х+7х2 = в) (х+2)2у-7(х+2) = г) 4(а-7)+9а(а-7) = д) 3(а-4)+5с(4-а)= |