ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 95
Скачиваний: 1
Присваиваем найденный ближайший кластер тому, для которого вызвана функция
3) Пока число кластеров больше заданного при запуске алгоритма
3.1) Найти индекс кластера, который можно объединить с соседом
Для всех кластеров
Берем найденную на предыдущем запуске цикла дистанцию (или очень большое число при первом запуске)
Находим новую минимальную дистанцию
3.2) Создаем новый кластер из двух соседей
3.3) Пересчет связей в списке кластеров
Для всех кластеров
Дистанция до нового кластера
Если найденная дистанция меньше самой близкой
Объявляем кластер ближайшим соседом нового
Если ближайший кластер текущего был одним из объединённых
Если этот кластер ближе, чем новая минимальная дистанция
Присваиваем ему новый ближайший
Если нет
То самый ближайший к нему новый, объединённый
Если не был
Если его ближайший сосед дальше, чем новый кластер
То самый ближайший к нему новый, объединённый
3.4) Добавляем новый кластер в список
На выходе получаем n кластеров
Второй шаг алгоритма.
Берётся весь датасет, и сканируется каждая его точка. Каждая точка присваивается к самому ближайшему кластеру (на основании расчета расстояния до всех его точек представителей)
Финальная кластеризация
1) Словарь для n кластеров
2) Для всех точек в массиве
Подбираем к какому классу принадлежит точка
Для всех кластеров
Минимальная дистанция = большое число
Минимальное расстояние от точки до кластера
Если дистанция меньше, чем минимальная
Минимальная дистанция = новая минимальная дистанция
Возвращаем индекс кластера, для которого дистанция минимальна
Присваиваем в словарь, в массив одного из классов
3) Возвращаем массивы индексов точек распределенные по классам
На выходе получаем кластеризованный набор данных.
Программная реализация на языке
Python с использованием библиотеки pyclustering.import osimport randomimport numpy as npimport matplotlib.pyplot as pltdef euclidean_distance(x, y):return np.sqrt(np.sum((x - y) ** 2))def get_representatives(data, k, fraction):# Select k random points as initial representativesrepresentatives = data[np.random.choice(data.shape[0], size=k, replace=False), :]# Find additional representatives by clustering with single linkagewhile k < int(fraction * data.shape[0]):dist_matrix = np.zeros((k, data.shape[0]))for i in range(k):for j in range(data.shape[0]):dist_matrix[i][j] = euclidean_distance(representatives[i], data[j])min_dist = np.min(dist_matrix, axis=0)max_index = np.argmax(min_dist)representatives = np.vstack((representatives, data[max_index]))k += 1return representativesdef get_clusters(data, representatives, alpha):clusters = [[] for _ in range(representatives.shape[0])]for i in range(data.shape[0]):min_dist = np.infmin_index = -1for j in range(representatives.shape[0]):dist = euclidean_distance(data[i], representatives[j])if dist < min_dist:min_dist = distmin_index = jclusters[min_index].append({'index': i, 'data': data[i]})# Merge clusters that are closer than alphawhile True:merged = Falsefor i in range(representatives.shape[0]):for j in range(i + 1, representatives.shape[0]):dist = euclidean_distance(representatives[i], representatives[j])if dist < alpha:merged = Truenew_rep = (len(clusters) + len(clusters[j])) / (len(clusters[i]) + len(clusters[j])) * \representatives[i] \+ (len(clusters) + len(clusters[i])) / (len(clusters[i]) + len(clusters[j])) * \representatives[j]representatives[i] = new_repclusters[i] += clusters[j]del clusters[j]representatives = np.delete(representatives, j, axis=0)breakif merged:breakif not merged:breakreturn clustersif __name__ == '__main__':# Generate random datanp.random.seed(0)data = np.random.randn(100, 2)# Clear previous console outputos.system('cls' if os.name == 'nt' else 'clear')# Print initial Dataprint(f'Data: {data}\n')# Clustering parametersk = 5fraction = 0.1alpha = 0.5# Plot parameterspoint_size = 15# Cluster data using CURErepresentatives = get_representatives(data, k, fraction)clusters = get_clusters(data, representatives, alpha)# Create a new figure and axisfig, ax = plt.subplots()# Print resultsprint(f'Representatives: {representatives}\n')for i, cluster in enumerate(clusters):print(f'Cluster {i}: {cluster}')# Extract the points from the cluster dictionarypoints = [p['data'] for p in cluster]points = np.array(points)# Generate a random color for the clustercolor = tuple(random.uniform(0, 1) for _ in range(3))# Plot the pointsax.scatter(points[:, 0], points[:, 1], c=color, s=point_size, label=f'Cluster {i}')# Set the axis labels and legendax.set_xlabel('x')ax.set_ylabel('y')ax.legend()# Show the plotplt.show()Результат работы программы:Определим входные данные, которые мы будем использовать для нашего алгоритма кластеризации. 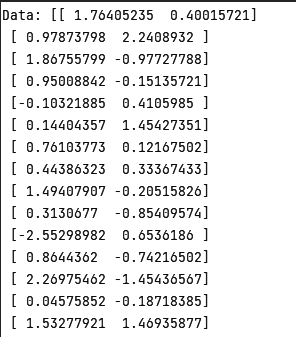Всего определяется 100 точек в двумерном пространстве.Далее из них выбирается несколько точек, которые будут поданы на вход алгоритма для начала кластеризации.
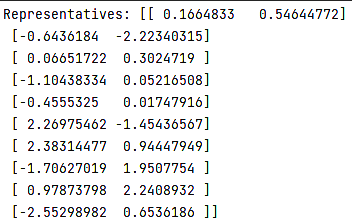
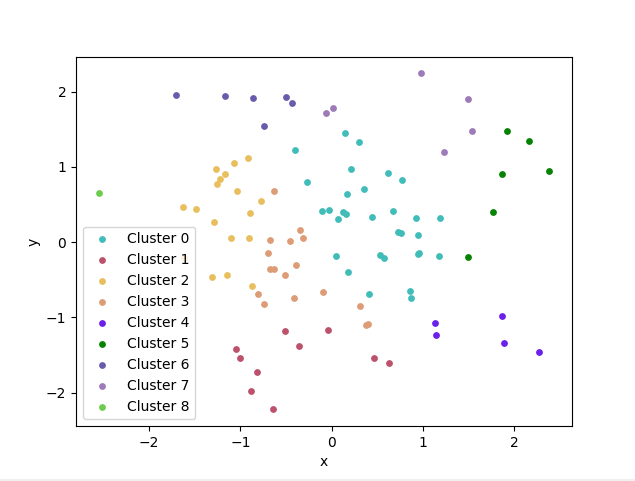
В результате видим список кластеров и точек, которые были к ним причисленыВизуальное отображение кластеров:Источники:
-
https://digitrain.ru/articles/13812/ -
https://translated.turbopages.org/proxy_u/en-ru.ru.49047d43-63b9b6b3-9378cf2d-74722d776562/https/en.wikipedia.org/wiki/Cure_data_clustering -
https://algowiki-project.org/ru/Участник:JuliaA/Алгоритм_кластеризации_с_использованием_представлений -
https://russianblogs.com/article/6919119054/ -
https://www.ijirmf.com/wp-content/uploads/IJIRMF202006027.pdf