Файл: Сабаты таырыбы Сызыты тедеулер жйесін Крамер жне Гаусс дісімен шешу Сабаты масаты Білімділік.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.01.2024

Просмотров: 12

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Сабақтың тақырыбы: Сызықтық теңдеулер жүйесін Крамер және Гаусс әдісімен шешу

Сабақтың мақсаты: Білімділік: Оқушыларға сызықтық теңдеулер жүйесін Крамер және Гаусс әдістері оынша шешуге болатындығын түсіндіру, Крамер, Гаусс әдістерін нақты түсіндіру теоремасын беру.

Тәрбиелік: Крамер, Гаусс өмірбаяндарынан үзінді келтіріп ғылыми көзқараста тәрбиелеу.
Дамытушылық: сызықтық теңдеулер жүйесінің шешу әдістерінің түрлерімен байланыстырып, өздеріне жеңіл және шапшаң есептеу әдістерін дамыту.
Сабақтың көрнекілігі: Крамер әдісі сызылған плакат, үлестірмелі материалдар,

Сабақтың типі: жаңа білімді меңгерту сабағы

Сабақтың түрі: практикалық (өз бетімен жұмыстану)
Сабақтың барысы: а) Ұйымдастыру.

б) Үй тапсырмасын тексеру .

в) Жаңа сабақты түсіндіру және бекіту.

г) Қорытындылау.

д) Үйге тапсырма.


а-а: (Крамер теоремасы) Егер берілген сызықтық теңдеулер жүйесінің анықтауышы 0-ге тең емес болса, онда берілген жүйенің тек қана бір шешімі болады. Оларды мына формулалар арқылы таабмыз
X = ∆x y = ∆y z = ∆z (1)

∆ ∆ ∆

Мұндағы: ∆ - берілген жүйенің анықтауышы
∆ = 0

∆x = , ∆y =
∆z =


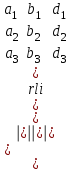
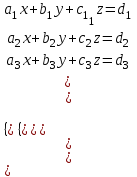
Мысалы:

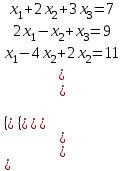
Крамер әдісі бойынша теңдеуді шешу керек.
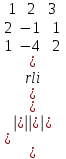∆ = = -2 + 2 – 24 + 3 – 8 + 4 = - 25

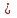∆ 0, ендеше теңдеудің бір шешімі бар.
∆1 = 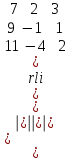= -14 + 22 – 108 + 33 – 36 + 28 = - 75

∆ 2 = 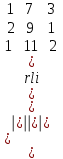= 18 + 7 + 66 – 27 – 28 – 11 = 25
∆ 3 = 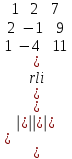= -11 + 18 – 56 + 7 – 44 + 36 = -50
X1 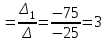X2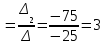

X3 = 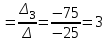ж/бы: (3; -1; 2)
Гаусс әдісі бойынша берілген жүйенің матрицасын баспалдақ түрге келтіру немесе біртіндеп жою әдісі болып табылады.
Мысалы:

Матрица түріне келтіреміз және Гаусс әдісі бойынша шешеміз.

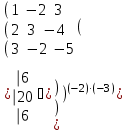
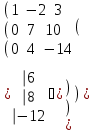
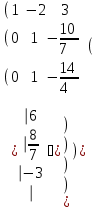-1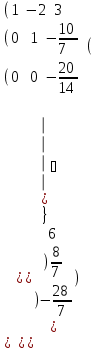

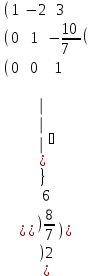
Сонымен z =2











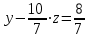
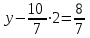
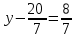
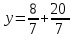
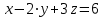
x = 8 ж/бы: (8; 4; 2)
Мысалы:


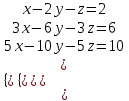
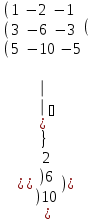
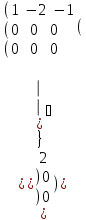
x- 2y – z=2 шешімі көп
№ 129.

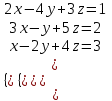
Матрица түрінде жазып Фаус әдісін қолдану және теңдеуді шешу.

:

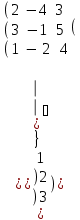
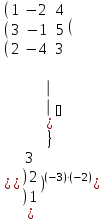
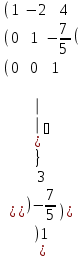
Z = 1





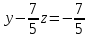
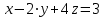
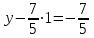
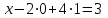
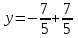x = -1

y = 0 ж/бы: (-1; 0; 1)


  1. Крамер әдісі дегеніміз не?

  2. Фаусс әдісі дегеніміз не?


Үйге: №136, 138, 145,

(П.Т. Апаносов 115-116 бет).

Смотрите также файлы