1 КОНТРОЛЬНАЯ РАБОТА №1

Крупенев Илья

Вариант 8

Вопросы: 4; 18; 36. Задачи: 1.5; 2.9; 3.11
1.1 Вопрос 4


Что такое объёмный вес жидкости и как он связан с плотностью жидкости?

Ответ:

Объем­ный вес вес жидкости G, приходящийся на единицу объема V:

Для определения объемного веса жидкости в данной точке следует пользоваться формулой

Так как 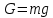, то плотность и объемный вес связаны между собой соотношением
Плотность, а, следовательно, и объемный вес жидкости меняются с изменением давления и температуры.
1.2 Вопрос 18


Что понимают в гидравлике под идеальной жидкостью?

Ответ:

Жидкостью называют идеальной в тех случаях, когда при исследовании пренебрегают теми или другими, важными для исследуемого вопроса, ее физическими свойствами. Характеризуется:

а) абсолютной неизменяемостью объема (при изменении давления и температуры)

б) полным отсутствием вязкости, т.е. сил трения при любом ее движении.

Таким образом, идеальная жидкость – это жидкость, лишенная внутренних сил трения.
1.3 Вопрос 36


В чем состоит сущность закона Архимеда?

Ответ:

Сила давления покоящейся жидкости на погруженное в нее тело, равна весу жидкости в объеме, вытесненном телом, направлена по вертикали вверх и приложена в центре тяжести этого объема. Это есть формулировка закона Архимеда. Закон Архимеда можно записать в виде

где сила Архимеда, Н;

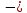плотность жидкости, ;

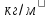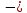объем тела, погруженного в жидкость, .

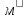На тело, погруженное в жидкость, также действует сила тяжести тела. И поведение тела в жидкости зависит от соотношения между модулями силы тяжести 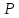и силы Архимеда 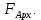Возможны следующие три случая:

1) 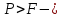тело тонет;

2) 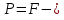тело плавает в жидкости;

---

3) 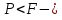тело всплывает до тех пор, пока не начнет плавать.

На практике применяются все три случая. В первом случае применяется для погружения в воду подводных судов, второй случай - плавание надводных судов и третий случай - для всплытия подводных судов на поверхность.

1.4 Задача 1.5

Определить плотность воды при температуре 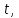если при температуре 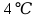плотность воды 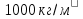. Сравнить с табличными значениями. Коэффициент температурного расширения принять равным .

Дано:

Решение:

Для определения плотности воды при заданной температуре применим приближенное соотношение для расчета изменения плотности капельных жидкостей с изменением температуры:


где плотность жидкости при температуре

плотность жидкости при температуре

коэффициент температурного расширения.

Вычисляем

Из таблицы 1 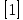при 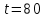плотность воды составляет
Погрешность расчета составляет

Ответ:

1.5 Задача 2.9

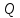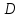Определить усилие , создаваемое большим поршнем гидравлического пресса, если на малый поршень действует сила . Диаметры поршней и 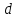, а разность уровней жидкостей 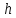. Плотность масла принять равной 800

Дано:

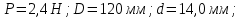
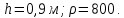
Решение:


В качестве поверхности уровня (поверхности равного давления) принимаем горизонтальную плоскость 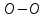, проходящую через точк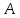и и 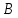. Так как давление в любой точке поверхности уровня величина постоянная, то

,где

Тогда


Вычисляем
Ответ:


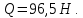
1.6 Задача 3.11

Определить вертикальную и горизонтальные составляющие силы давления воды на 1 метр ширины указанной криволинейной поверхности, если заданны значения 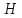и .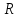

Показать направления действия сил.

Дано: ;

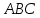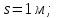
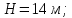
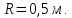
Решение:


Принимаем плотность воды

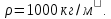
Горизонтальная составляющая силы давления на криволинейную поверхность 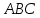равна силе суммарного давления жидкости на вертикальную проекцию этой стенки:

где глубина погружения центра тяжести вертикальной проекции стенки.

Вертикальной проекцией данной криволинейной поверхности является прямоугольник со сторонам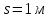и и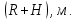

Тогда .

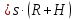Глубина погружения



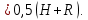
В таком случае

Вертикальная составляющая равна весу жидкости в объеме тела давления:
где 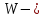объем тела давления.

Телом давления называется объем жидкости, ограниченный данной криволинейной поверхностью, вертикальной плоскостью проведенной через нижнюю образующую криволинейной поверхности, и свободной поверхностью жидкости. Поскольку объем находится со смачиваемой стороны стенки, вес тела считаем положительным (направленным вниз).

В нашем случае телом давления является фигура , состоящий из параллелепипеда и четверти цилиндра

Вычисляем

Ответ:

2 КОНТРОЛЬНАЯ РАБОТА №2

Крупенев Илья

Вариант 8

Вопросы: 4; 18; 36; 48; 60. Задачи: 4.5; 5.9; 6.11; 7.9
2.1 Вопрос 4


Что называется линией тока?

Ответ:

Линией тока (рис. 1) называется линия, проходящая через последовательно движущиеся одна за другой частицы жидкости, векторы скоростей которых направлены по касательным к этой линии .


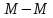2.2 Вопрос 18


Какая разница между средней и местной скоростью?

Ответ:

Скорость течения 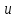, называемая местной скоростью, в разных точках живого сечения различны, то есть

В связи с этим, для упрощения расчетов в случаях параллельноструйного и плавно изменяющегося движений вводят понятие средней для данного живого сечения скорости течения. Эту скорость (фиктивную, в действительности не существующую) принято обозначать . Скорость

определяется соотношением

Здесь 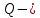расход жидкости, проходящий через живое сечения площадью

Скорость является гидравлической характеристикой живого сечения потока.
2.3 Вопрос 36


Приведите порядок расчета перепада давлений в коротком трубопроводе при известных значениях расхода и диаметра?

Ответ:

При расчетах перепада давлений в коротком трубопроводе необходимо учитывать местные потери. В таком случае потери давления находят из уравнения


где коэффициент гидравлического терния;

длина трубопровода диаметра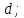

суммарный коэффициент местных сопротивлений на участке трубопровода;

плотность жидкости;

скорость движения жидкости в трубопроводе.

Скорость движения жидкости

где 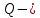объемный расход жидкости;

площадь поперечного сечения трубопровода диаметром .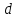
Площадь сечения
Тогда

Коэффициент гидравлического трения зависит от режима движения жидкости.

Турбулентный режим

где безразмерное число Рейнольдса, характеризующее режим движения жидкости;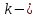

абсолютный коэффициент шероховатости стенок трубы;

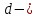диаметр трубы.

Ламинарный режим
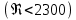
Числе Рейнольдса
где 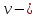коэффициент кинематической вязкости жидкости.
2.4 Вопрос 48


Каким образом определяются потери давления на трение в трубах некруглого сечения?

Ответ:

Потери давления по длине определяются по формуле



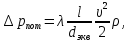
где 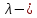гидравлический коэффициент трения;

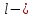длина трубопровода, м;

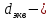эквивалентный диаметр трубопровода, м;

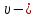скорость движения жидкости в трубопроводе,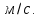

Для ламинарного режима гидравлический коэффициент трения определяется из выражения



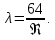
Для турбулентного режима по обобщенной формуле Альтшуля



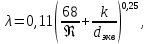
где 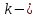абсолютная шероховатость стенок трубы, м.

Здесь 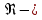безразмерное число Рейнольдса.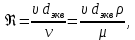



где 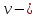коэффициент кинематической вязкости,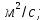

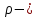плотность жидкости,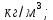

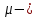коэффициент динамической вязкости,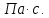

Эквивалентный диаметр определяют по формуле



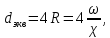
где 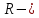гидравлический радиус, м;

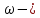площадь живого сечения,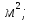

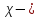смоченный периметру, м.
2.5 Вопрос 60

Какова причина увеличения расхода при истечении через наружный цилиндрический насадок (по сравнению с отверстием в тонкой стенке).

Ответ:

Насадок, представляет собой короткую трубку, приставленную к отверстию, длина которой в 3,5–4 раза больше диаметра отверстия. Струя при выходе из отверстия в насадок сжимается, но приставленной его длине успевает расширяться и вытекает полным сечением. В связи с резким расширением струи в насадке получается дополнительная потеря напора, которая, в основном обуславливает снижение скорости. Вместе с тем площадь выходного живого сечения в случае насадка (по сравнению с площадью сжатого сечения при истечении из отверстия) увеличивается. Так как расход 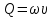, то расход в случае насадка (по сравнению с расходом при истечении из отверстия) должен увеличиваться.
2.6 Задача 4.5

По прямоугольному вентиляционному каналу размером 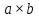за время 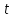подается объем воздуха 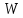. Определить скорость воздуха, гидравлический радиус и эквивалентный диаметр.

Дано: .

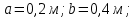
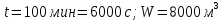Решение:

Гидравлический радиус канала равен



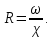
Здесь 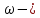площадь поперечного сечения канала; 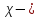смоченный периметр.

Площадь сечения канала



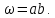
Смоченный периметр канала



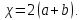
Тогда



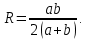
Эквивалентный диаметр равен



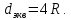
Расход жидкости, проходящий по каналу



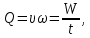
где 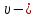скорость потока;

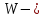объем воздуха, проходящего по каналу за время .
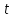Тогда



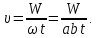
Вычисляем







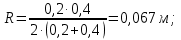
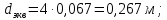
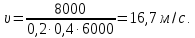
Ответ: ;

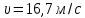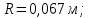
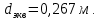
2.7 Задача 5.9

Насос перекачивает воду по трубопроводу диаметром 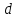на высоту 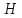с расходом 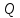. Давление на выходе из насоса 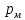, в баке 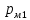. Потери напора в трубопроводе рассчитываются по формул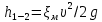е , где 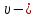скорость в трубе, а 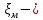коэффициент сопротивлений.

Р 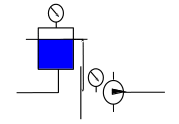ассчитать коэффициент сопротивлений .


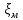Дано: ; ; ;

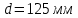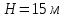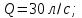
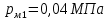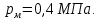
Решение:

Плотность воды принимаем .

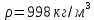Составляем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0:



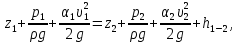
где 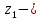геометрический уровень сечения 1-1,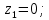

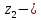геометрический уровень сечения 2-2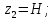

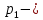давление в сечении 1-1,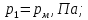

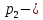давление в сечении 2-2,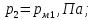

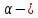коэффициент Кориолиса (коэффициент режима движения жидкости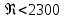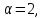) при при 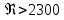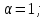принимаем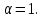

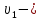скорость жидкости в сечении 1-1,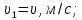



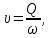
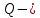расход жидкости,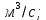

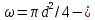площадь сечения трубы,



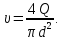
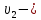скорость жидкости в сечении 2-2,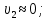

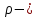плотность жидкости,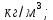

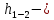потери напора на гидравлические сопротивления между сечениями 1-1 и 2-2, м.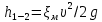



Тогда





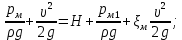
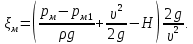
Вычисляем




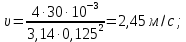
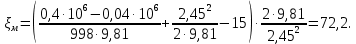
Ответ:

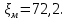
2.8 Задача 6.11

Дан участок длинного водопровода ( 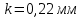), состоящий из трех последовательно соединенных новых стальных трубопроводов разного диаметра. Расход воды 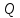; диаметры условного прохода труб: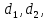 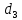; длина трубопроводов: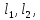 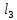. Определить величину потерь напора на участке. Построить напорную линию, если напор в начале трубопровода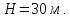

Дано: ; ; ; ;

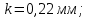
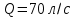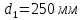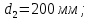
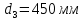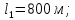
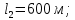
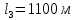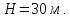
Решение:

Расход на всем участке трубопровода будет постоянным, то есть



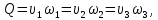
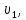
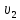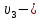где и скорости потока жидкости в поперечных сечениях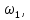 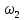и 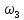участка трубопровода.

Площади сечений



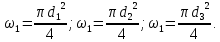
Тогда



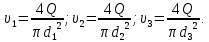
Потери напора на участке складывается их потерь напора по длине и местных потерях на каждом участке. Тогда



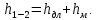
Потери напора по длине



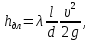
где 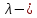гидравлический коэффициент трения;

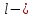длина трубопровода диаметром ;

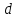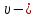скорость потока жидкости в трубопроводе.

В нашем случае





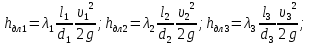
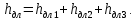
Для определения коэффициента гидравлического трения при 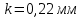применяем данные табл. 23 [1].

при





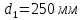
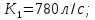
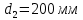
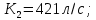
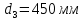
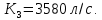
Здесь 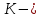модуль расхода.

Модуль расхода вычисляется по формуле:



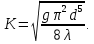
В таком случае, коэффициент гидравлического трения



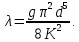
Для каждого участка



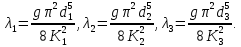
Местные потери напора складываются и потерь на внезапное сужение потока 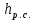и внезапное расширение потока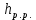



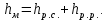
Внезапное сужение потока



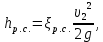
где 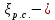коэффициент сопротивления на внезапном сужении трубопровода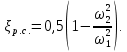



Тогда



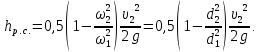
Внезапное расширение потока (формула Борда)



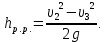
Вычисляем
























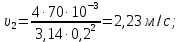
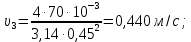
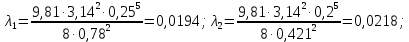
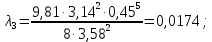
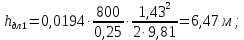
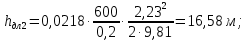
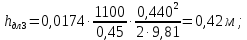
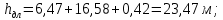
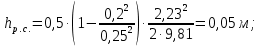
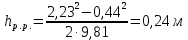
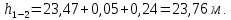
Строим напорную линию
Ответ:




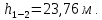
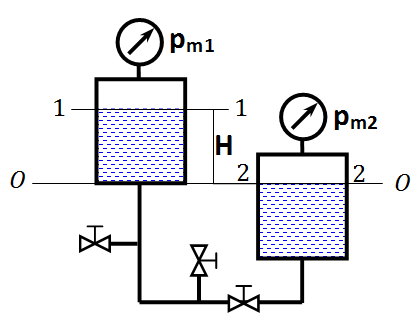
2.9 Задача 7.9

Вода перетекает из левого бака в правый по трубопроводу длиной 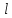, диаметром 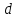и шероховатостью поверхности трубы 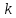. Расход воды 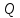. Разность уровней воды в баках 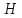. Коэффициент местных сопротивлений 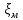. Манометрические давления в баках 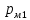и .

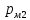Рассчитать давление .

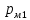Дано: ; ; ; ; ; ; ; .

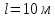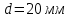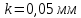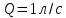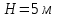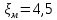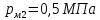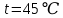Р ешение:


При температуре воды 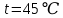из справочных данных находим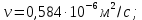



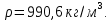
Составляем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0:



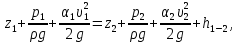
где 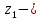геометрический уровень сечения 1-1,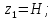

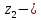геометрический уровень сечения 2-2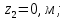

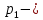давление в сечении 1-1,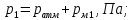

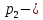давление в сечении 2-2,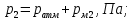

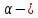коэффициент Кориолиса (коэффициент режима движения жидкости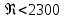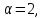) при при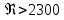

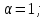
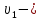скорость жидкости в сечении 1-1,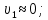

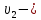скорость жидкости в сечении 2-2,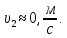

Скорость жидкости в трубе



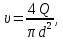
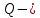объемныйрасход жидкости в трубопроводе,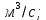

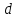− диаметр трубопровода, м;

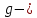ускорение свободного падения,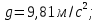

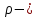плотность жидкости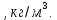

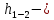потери напора на гидравлические сопротивления между сечениями 1-1 и 2-2, м;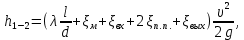



где 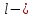длина трубопровода, м;

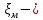коэффициент местных сопротивлений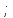

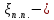коэффициент местных сопротивлений при плавном повороте на 90 , ;

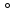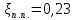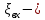коэффициент местных сопротивлений при входе в трубу, ;

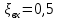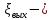коэффициент местных сопротивлений при выходе из трубы, ;

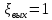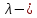коэффициент гидравлического трения в трубопроводе.

При турбулентном режиме движения воды 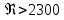коэффициент гидравлического трения рассчитывается по формуле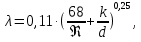



где 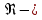число Рейнольдса,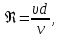



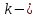эквивалентная шероховатость трубы.

Тогда





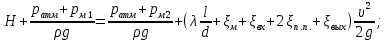
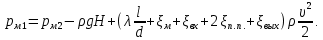
Вычисляем










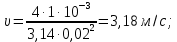
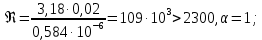
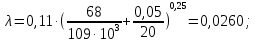
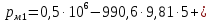
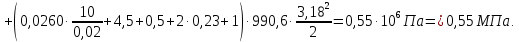
Ответ:

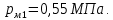
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. 
   Альтшуль, А. Д. Гидравлика и аэродинамика (основы механики жидкости) [Текст] / А. Д. Альтшуль, П. Г. Киселев. – Москва : Стройиздат, 1965. – 275 с.
   
2. 
   Гидравлика [Текст] : учебное пособие / Е. З. Рабинович. – Москва : Недра, 1980. – 278с.
   
3. 
   Пятибрат, В. П. Гидравлика. Задания на расчѐтно графическую работу для студентов дневной формы обучения [Текст] : Методические указания / В. П. Пятибрат. – Ухта : УГТУ, 2016. – 36 с., ил.
   

---

Смотрите также файлы

• Строение атома.docx

• Грушина Оксана Алексеевна Место работы боу Андреевская ош общая информация по уроку класс укажите класс, к которому относится урок.docx

• Тема Обязательства родителей перед детьми и обязательства детей перед родителями.docx

• Семинар. Тема Ресурсный потенциал и отраслевая структура мировой экономики. Задание 2.docx

• Сочинительные ряды в синтаксическом строе романа Лермонтова Герой нашего времени.docx