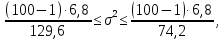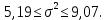ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 4
Тема 1.9. Построение интервальных оценок.
Формулировка задания. Найти 95-процентные интервальные оценки математического ожидания и дисперсии для данных практического задания 3, если известно, что выборка произведена из нормально распределенной генеральной совокупности.
Образец выполнения задания
Задание
Найти интервальные оценки математического ожидания и дисперсии, если известно, что выборка произведена из нормально распределенной генеральной совокупности.
| Урожайность, ц/га | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | 20–22 |
| Количество участков | 6 | 12 | 33 | 22 | 19 | 8 |
Решение
В данной задаче математическое ожидание и дисперсия, поэтому для определения интервальных оценок используются формулы:
-
доверительный интервал математического ожидания при неизвестной дисперсии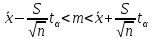
; -
доверительный интервал дисперсии при неизвестном математическом ожидании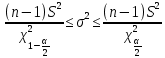
.
В формулах используются среднее арифметическое и выборочная дисперсия, поэтому построим таблицу для их вычисления.
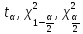– критические точки, для определения которых используются соответствующие таблицы. Критическая точка
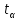определяется по таблице критических точек распределения Стьюдента по уровню значимости α = 1– γ и степени свободы n–1, γ – доверительная вероятность. По условию γ = 0,95, значит, α = 0,05 и
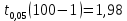. Критические точк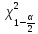и
и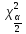 
определяются по таблице критических точек
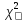– распределения по уровню значимости α и степени свободы n –1. 
; 
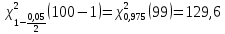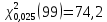;| Середина интервала xi | Частота ni |  |  |  |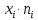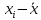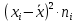
| 11 | 6 | 66 | –5,2 | 162,24 |
| 13 | 12 | 156 | –3,2 | 122,88 |
| 15 | 33 | 495 | –1,2 | 47,52 |
| 17 | 22 | 374 | 0,8 | 14,08 |
| 19 | 19 | 361 | 2,8 | 148,96 |
| 21 | 8 | 168 | 4,8 | 184,32 |
| Сумма | 100 | 1620 | | 680 |
; 
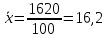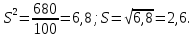
Доверительный интервал для математического ожидания:
,
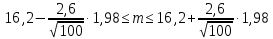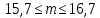.Доверительный интервал для дисперсии:
