ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 74
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание № 4.
Модели управления запасами
Цель работы: освоить и закрепить практические навыки по использованию моделей управления запасами.
Краткиетеоретическиесведения
Общие определения
Запасаминазывается любой ресурс на складе, который используется для удовлетворения будущих нужд. Примерами запасов могут служить полуфабрикаты, готовые изделия, материалы, различные товары, а также такие специфические товары, как денежная наличность, находящаяся в хранилище. Большинство организаций имеют примерно один тип системы планирования и контроля запасов. В банке используются методы контроля за количеством наличности, в больнице применяются методы контроля поставки различных медицинских препаратов.
Существуют многие причины, побуждающие организации создавать запасы.
Существует проблема классификации имеющихся в наличии запасов. Для решения этой задачи используется методика административного наблюдения. Цель ее заключается в определении той части запасов предприятия, которая требует наибольшего внимания со стороны отдела снабжения. Для этого каждый компонент запасов рассматривается по двум параметрам: а) его доля в общем количестве запасов предприятия; б) его доля в общей стоимости запасов предприятия.
Методика20/80.в соответствии с этой методикой компоненты запаса, составляющие 20% его общего количества и 80% его общей стоимости, должны отслеживаться отделом снабжения более внимательно.
Методика ABC: в рамках этой методики запасы
, имеющиеся в распоряжении предприятия, разделяются на три группы: группу А (10% общего количества запасов и 65% его стоимости); группу В (25% общего количества запасов и 25% его стоимости); группу С (65% общего количества запасов и около 10% его стоимости).
Необходимо отметить, что классификация запасов может быть основана не только на показателях доли в общей стоимости и в общем количестве. Преимущества методики деления видов запасов на классы заключаются в возможности выбора порядка контроля и управления для каждого из них.
Рассмотрим определяющие понятия теории управления запасами.
Издержкивыполнениязаказа(издержки заказа) – накладные расходы, связанные с реализацией заказа. В промышленности такими издержками являются затраты на подготовительно-заготовочные операции.
Издержки хранения – расходы, связанные с физическим содержанием товаров на складе, плюс возможные проценты на капитал, вложенный в запасы. Обычно они выражаются или в абсолютных единицах, или в процентах от закупочной цены и связываются с определенным промежутком времени.
Совокупные издержки за период представляют собой сумму издержек заказа, издержек хранения и упущенного дохода. Иногда к ним прибавляются издержки на покупку товаров.
Сроквыполнениязаказа– срок между заказом и его выполнением. Точка восстановления – уровень запаса, при котором делается новый заказ.
Краткая характеристика моделей управления запасами
-
Модель оптимального размера заказа
Предпосылки: 1)темп спроса на товар известен и постоянен; 2) получение заказа мгновенно; 3) отсутствуют количественные скидки при закупке больших партий товара; 4) единственные меняющиеся параметры – издержки заказа и хранения; 5) исключается дефицит в случае своевременного заказа.
Исходные данные: темп спроса, издержки заказа и хранения.
Результат: оптимальный размер заказа, время между заказами и их количество за период.
-
Модель оптимального размера заказа
в предположении, что получение заказа не мгновенно
Следовательно, нужно найти объем запасов, при котором необходимо делать новый заказ.
Исходные данные: темп спроса, издержки заказа и хранения, время выполнения заказа.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса.
Рассмотрим подробнее модели с фиксированным размером заказа.
Модель 1. Наиболее экономичного размера заказа. Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис.4.1).
Пусть
Q – размер заказа;
Т – протяженность периода планирования;
D – величина спроса за период планирования;
d – величина спроса в единицу времени;
К – издержки заказа;
Н – удельные издержки хранения за период;
Тогда:
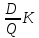– совокупные издержки заказа; 
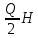– совокупные издержки хранения; 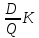+ 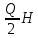– суммарные издержки заказа; d =
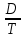; Q* =
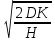– оптимальный размер заказа; N =
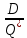– оптимальное число заказов за период;t* =
= 
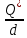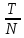– время цикла (оптимальное время между заказами).
Q*Рис. 4.1. Модель 1. Наиболее экономичного размера заказа
Модель 2.Введем предположение о том, что заказ может быть получен не мгновенно, а с течением времени. Тогда нам необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе. Следовательно, нам необходимо найти тот уровень запасов, при котором делается новый заказ.
Этот уровень называется точкой восстановления R.
Пусть L - время выполнения заказа. Тогда R = величина спроса в единицу времени, умноженная на время выполнения заказа = d L.
Другие характеристики системы определяются так же, как и в модели 1. Модель иллюстрируется рис.4.2.
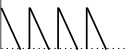Q*Рис. 4.2. Модель 2
Пример
№1
Андрей является торговым агентом компании VOLVO и занимается продажей последней модели этой марки автомобиля.
Годовой спрос оценивается в 4000 ед. Цена каждого автомобиля равна 90 млн. р., а годовые издержки хранения составляют 10% от цены самого автомобиля.
Андрей произвел анализ издержек заказа и понял, что средние издержки заказа составляют 25 млн. р. на заказ. Время выполнения заказа равно шести дням. В течение этого времени ежедневный спрос на автомобили равен 20.
Необходимо в процессе решения данного примера ответить на следующие вопросы:
-
Чему равен оптимальный размер заказа? -
Чему равна точка восстановления? -
Каковы совокупные издержки? -
Каково оптимальное количество заказов в год? -
Каково оптимальное время между двумя заказами, если предположить, что количество рабочих дней в году равно 200?
Ниже приведено описание исходных данных и результаты решения контрольного примера с использованием условных обозначений:
Исходные данные:
величина спроса за год D=4000;
издержки заказа К = 25; издержки хранения = 9;
цена за единицу с = 90;
время выполнения заказа L=6; ежедневный спрос d= 20;
число рабочих дней Т = 200.
Решение:
оптимальный размер заказа Q* = 149;
точка восстановления R = 120 ;
число заказов за год N = 26,83;
совокупные издержки С = 1341 (149*9);
стоимость продаж = 360000 (4000*90);
число дней между заказами t = 7,45.
Индивидуальные задания