Лекция 1

Основные понятия теории вероятностей

Случайные события и их классификация.

Теория вероятностей – это раздел математики изучающий закономерности в случайных явлениях и процессах. Случайное явление – это явление, которое при повторении опыта протекает каждый раз по иному. Опыт (испытание) – целенаправленная, запланированная деятельность человека, как правило, неоднократно повторяемая, с целью изучения законов природы. Событие (исход) – всякий факт, который может произойти в результате некоторого опыта. Случайное событие – событие, которое в результате опыта может произойти, а может не произойти. Достоверное событие – событие, которое при всех испытаниях в данном опыте обязательно наступает. Невозможное событие – событие, которое в данном опыте никогда не наступает. Несовместные события – это события, которые никогда не появляются совместно в одном опыте. Совместные события – это такие события, когда появление одного события А не исключает появление другого события В в одном опыте. Равновозможные события – ни одно из событий не является более возможным, чем остальные. Полная группа событий. События образуют полную группу событий, если в результате опыта одно из них обязательно реализуется. То есть, они в совокупности занимают все пространство элементарных событий. Противоположные события можно рассматривать как частный случай полной группы событий с n = 2 .

Перестановки. Пусть упорядоченное множество А состоит из n элементов. Тогда количество способов различных размещений этих элементов на n мест (или по-другому, количеством способов выбора n элементов из n) называется перестановкой и определяется

Статистическая вероятность и частота событий. Если опыт не сводится к “схеме случаев”, например, кость со смещенным центром тяжести, то вероятность события определить так просто, как мы делали выше невозможно. Однако есть другой способ подсчета применяемый на практике. Производится n опытов, в каждом из которых заданное событие А появляется или не появляется. Относительной частотой события А в данной серии опытов называется отношение числа опытов, в которых событие А происходит, к числу всех опытов. Если m число опытов, где появилось А и n число опытов, то частота события А определяется P(A)=m/n. В отличие от классического определения вероятности частоту событий будем отмечать звездочкой. Статистической вероятностью называют предел к которому стремится относительная частота события А, при неограниченном увеличении числа опытов (n стремится к бесконечности ). Так как на практике число опытов всегда конечно, то относительная частота события будет только приближенной оценкой его вероятности.

---

Геометрическая вероятность. В ряде практических задач число возможных исходов бесконечно (пространство элементарных событий несчетно), что делает невозможным применение классического определения вероятностей. Однако, если остается в силе понятие равновозможности событий, то применяется так называемый геометрический метод подсчета вероятности.

Лекция 2

Алгебра событий.

Пересечением двух событий А и В называется событие С, состоящее в совместном выполнении событий А и В. Логическое умножение – это пересечение множеств А и В. Заметим, что наряду с операциями сложения и умножения можно ввести операцию логического вычитания (исключения) ABC или A/BC , состоящее в том, что происходит событие А, а событие В не происходит. Теорема сложения вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий P ABPAPB.

Докажем это, представив элементарные события точками на линии



Пусть событию А благоприятны m – элементарных событий, то есть соответствуют m точек. Событию B благоприятны k – элементарных и соответствуют k точек на линии. Поскольку события несовместны, то подмножества m и k точек не пересекаются. Тогда, очевидно, событию A+ B благоприятны m+k элементарных событий, то есть m+k точек. Так как P(A)=m/n и P(B)=k/n, то P(A+B)=m/n+k/n=P(A)+P(B). Теорема умножения вероятностей. Прежде, чем ее сформулировать, введем два новых понятия о зависимых и независимых событиях. Событие А называют независимым (зависимым) от события В, если вероятность события А не зависит (зависит) от того, произошло событие В или нет. События А и В, как правило, относятся к разным временным интервалам и интерпретируются как звенья причинно-следственной цепочки. Одно из событий предшествует другому.

Условной вероятностью события В называют вероятность события В, вычисленную при условии того, что имело место событие А. Условие независимости событий А и В будет определяться P(B/A)=P(B) . Заметим, что если события А и В независимы, то они независимы попарно P(A/B)=P(A).

Теорема. Вероятность произведения двух совместных событий равна произведению вероятности одного из событий на условную вероятность другого при условии, что первое имело место. PABPA*PB/APB*PA/B.

Лекция 3

Теорема о полной вероятности событий.

Пусть требуется определить вероятность события А, которое может произойти вместе с одним из событий, несовместных и образующих полную группу. Будем называть эти события гипотезами.

---

Формула Байеса

Формула Бейеса показывает, как изменяется вероятность гипотезы P (Hi) при реализации события А. Таким образом определяем P=(A / Hi). Из теоремы умножения вероятностей следует непосредственно P(AHi)=P(Hi)P(A / H)=P(A)P(Hi / A)

Повторные испытания. Формула Бернулли.

На практике часто встречаются ситуации, когда один и тот же опыт повторяется неоднократно. В результате каждого опыта событие А или происходит, или не происходит. Зачастую нас интересует не исход отдельного опыта, а исход совокупности опытов. Например, при залпе батареи орудий, командира батарей интересует не кто конкретно попал в цель, а сколько вообще попаданий. Такие задачи довольно просто решаются для независимых опытов, когда вероятности исхода того или иного опыта не зависят от того, какие исходы имели предыдущие опыты. Таким образом, необходимо найти вероятность появления события А m раз в n опытах. Заметим, что независимые опыты могут проводиться в одинаковых условиях и в разных условиях.

Частная теорема. Если для одних и тех же условий производится n независимых опытов, в каждом из которых событие А появляется, с вероятностью р и не появляется с вероятностью q q  1  р , то вероятность появления события A m раз в n опытах находится по формуле Бернулли

P_n(m)=C^m_n p^mq^n-m

Лекция 4

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее какое именно. Случайная величина сопоставляется случайному событию.

Законы распределения случайных величин.

1. Ряд распределения для дискретных случайных величин.

2. Функция распределения как для дискретных, так и для непрерывных случайных величин.

3. Плотность функции распределения только непрерывных случайных величин.

Ряд распределения.

Рассмотрим прерывную случайную величину X, которая принимает значения x₁, x₂,x₃ …,x_n с возможными значениями вероятности P(x_n)=p_n

Функция распределения.

Для количественной характеристики непрерывных и прерывных случайных величин удобно пользоваться вероятностью события X  x . Таким образом, суммируются все предыдущие вероятности. Итак, функция распределения определяется как вероятность события X  x

F(x)=P(X x)

Свойства функции распределения:

функция Fx есть неубывающая функция своего аргумента. То есть F(x₂)  F(x₁

---

) для х₂  x₁ .

– F   0 . Характеризует невозможное событие.

– F 1 . Достоверное событие.

Числовые характеристики случайных величин.

Числовыми характеристиками случайной величины называют параметры, характеризующие самые существенные черты закона распределения этой величины. Очевидно, что самым первым параметром является среднее значение случайной величины, около которого и группируются ее значения.

Математическое ожидание

Математическим ожиданием случайной величины называется ее среднее значение, которое определяется как средневзвешенное или среднеарифметическое.

Модой называется наибольшее вероятное значение случайной величины.

Метод моментов

Моментное (приближенное) описание случайной величины широко используется в механике, физике, математической статистике и так далее. Моменты подразделяются на два вида:

– начальные моменты (приложены к началу координат),

– центральные моменты.

Лекция 5

Законы распределения случайных величин.

Биномиальное распределение

Случайная величина Х представляет собой число появлений события А в n независимых опытах и принимает целые неотрицательные значения. Вероятность появления события A m раз в n опытах определяется формулой Бернулли.

Распределение Пуассона

Дискретная случайная величина Х принимает целые неотрицательные значения 0, 1, 2, 3, …, n , где n достаточно большое число. Вероятность появления события в одном опыте P является достаточно малым числом. Однако,   np ограничено. Тогда случайная величина Х распределена по закону Пуассона

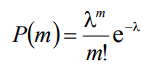P(m)=(л^m/m!)e^-л

Рассмотрим простейший поток событий, которые наступают в случайные моменты времени. Например, поступление сигналов вызова на автоматическую телефонную станцию. Поток называется стационарным, если вероятность появления k-событий за интервал времени t есть функция только k и t . Если события независимы, то поток обладает свойством отсутствия последействия. Если вероятность появления более одного события за малый промежуток времени значительно меньше вероятности появления только одного события, то поток обладает свойствами ординарности. Простейшим (пуассоновским) потоком называется поток событий, который обладает стационарностью, отсутствием последействий и ординарностью. Интенсивность потока  называется среднее число событий, которые появляются в единицу времени, где   np . Если   const , то вероятность появления k событий за время t будет

---

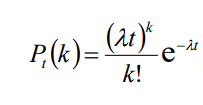
Геометрическое распределение.

Пусть производятся независимые испытания, в каждом из которых событие наступает с вероятностью p p  q 1 . Испытания заканчиваются, как только появится событие А. Вероятность этого события



Лекция 6

Система случайных величин.

Двухмерная случайная величина и законы ее распределения.

свойства функции распределения:

– Fx, y неубывающая функция обоих аргументов, Fx , y Fx , y 2  1 при 2 1 x  x ,     2 1 F x, y  F x, y при 2 1 y  y ;

– Fx,  F , y  0 (невозможные события);

– Fx  F x 1 ,  одномерная функция x;

– F y F y 2 ,  одномерная функция y;

– F, 1 ; – 0  Fx, y 1 ;

Условие независимости случайных величин

Случайная величина У называется независимой от случайной величины X, если закон распределения ее не зависит от того, какие значения примет случайная величина X. Для того, чтобы случайная величина У не зависела от случайной величины X, необходимо и достаточно выполнения условия Fx, y=F1x  F2y или fx, y = f1x  f2y. То есть должно выполняться f1x  f x/y 1 и f2y  f y/ x.

Зависимости случайных величин бывают двух типов – функциональные y  f x и стохастические (вероятностные). Если связь стохастическая, то можно указать закон распределения случайной величины Y в зависимости от того, какое значение приобретает случайная величина X. Вероятностные связи могут быть более или менее тесными. Тесные связи характеризуются большой вероятностью совместного появления случайных величин.

Моменты распределения

Начальным моментом порядков k, s системы двух случайных величин X,Y  называют математическое ожидание произведения x^k на y^s .

Центральным моментом порядков k, s для системы X,Y  называют математическое ожидание произведение центрированных случайных величин X и Y в степенях k и s , соответственно.

Коэффициент корреляции

Особую роль играет второй смешанный центральный момент. Он называется ковариацией двух случайных величин. Еще его называют корреляционным моментом.

Лекция 7

Основные теоремы о числовых характеристиках системы случайных величин.

Теорема 1. Математическое ожидание суммы случайных величин равна сумме их математических ожиданий. MX  Y  MX  MY.

---

Смотрите также файлы

• Усеченный конус и его элементы Цель урока знать определение усеченного конуса и его элементов уметь изображать усеченный конус на плоскости уметь решать задачи на нахождение элементов усеченного конуса. Задача 1.pptx

• Автономная некоммерческая органиация высшего образования волгоградский институт бизнеса центр по работе со студентами.docx

• Водные ресурсы Донбасса и их охрана.docx

• Заманауи апараттыкоммуникациялы технологияларды дамуы тенденциялары.docx

• Решение Пусть abADx.docx