ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №625
с углублённым изучением математики Невского района Санкт-Петербурга
имени Героя Российской Федерации В. Е. Дудкина
Учитель: Иванова Вера Юрьевна
Предмет: Геометрия
Класс: 8
Тема урока: «Вводный урок. Повторение программы 7 класса»
Номер урока: 1 урок
Тип урока: Урок обобщения, систематизации знаний.
Вид урока: Урок-беседа
Цель: обобщение и систематизация знаний, усвоенных в рамках курса геометрии в 7 классе.
Задачи:
-
Обучающие:
обобщить и систематизировать знания, усвоенные в рамках курса геометрии в 7 классе; устранить возможные пробелы в знаниях учащихся, сформировать понятие научной картины мира и представления о трансформации системы научных знаний; расширить кругозор учащихся в историческом аспекте;
-
Развивающие:
развивать логическое мышление, умения анализировать, сравнивать, обобщать, выделять главное, делать выводы; активизировать познавательную деятельность учащихся; развивать быстроту реакции, развивать память; развивать умение обучаться в сотрудничестве, работать в парах; развивать навыки логической математической речи; развивать умения учебного труда (умения работать в нужном темпе – писать, конспектировать, чертить);
-
Воспитательные:
воспитывать у учащихся интерес к геометрии, к познанию; воспитывать культуру речи и культуру общения.
Технологии:
-
Информационно-коммуникационные технологии; -
Технология развития «критического мышления»; -
Исследование в обучении; -
Обучение в сотрудничестве (работа в парах).
Оборудование:
Компьютер, мультимедийный проектор, экран, презентация в программе PowerPoint.
План урока:
-
Организационный момент. Проверка готовности учащихся. Сообщение темы и объяснение хода урока. Мотивация учебной деятельности. -
Актуализация и проверка знаний. Экскурс в историю. Мотивация и актуализация познавательной деятельности. -
Повторение теоретических основ геометрии (основных понятий, определений геометрических фигур, их свойств и аксиом). -
Работа (в парах). Блиц-опрос. -
Подведение итогов урока, оценка знаний учащихся. Домашнее задание.
Ход урока:
I. Построение курса геометрии
Слайд 1.
В 7 классе вы начали изучать новую для вас науку – геометрию.
Кто помнит, что означает «геометрия» в переводе с греческого? («гео» — «Земля» и «метрео» — «мерить»). Т.е. «землемерие».
Школьный курс делится на планиметрию и стереометрию.

Чем они отличаются? В планиметрии рассматривают свойства фигур на плоскости. Приведите примеры таких фигур (треугольники, четырехугольники).
В стереометрии изучают свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр.
II. Геометрия и история формирования научной картины мира
Слайд 2.
На входе в знаменитую Академию Платона была надпись:
«Не знающий геометрии пусть не входит сюда».
«Невежество – тяжкое бремя», - говорил древнегреческий философ и математик Фалес.
Каждый учёный древности, астроном, врач, философ, обязан был знать геометрию. Да и слов «математика», «алгебра» тогда ещё не было.
Слайд 3.
«Способ нелегкий сеченья цилиндров постичь не старайся…» - писал греческий математик, астроном, географ и поэт Эратосфен из Кирены, тот самый современник Архимеда, который с поразительно малой ошибкой измерил диаметр Земли. Пользуясь методами геометрии, он добился удивительного для того времени результата. Вычисленный им диаметр Земли оказался всего лишь, по некоторым данным, на 80 км меньше, чем фактический полярный диаметр.
ЭРАТОСФЕН (ок. 276 – 194 до н.э.)
Слайд 4.
О

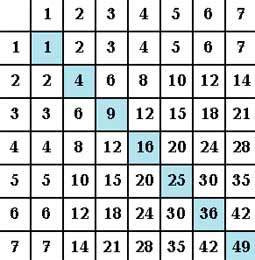 дин из самых популярных ученых за всю историю человечества – ПИФАГОР (прибл. 570 - 490 гг. до н. э.).
дин из самых популярных ученых за всю историю человечества – ПИФАГОР (прибл. 570 - 490 гг. до н. э.).Если сотни миллионов учеников умножить на сотни исписываемых ими тетрадей в клеточку, с каждой из которых смотрит на нас таблица Пифагора, т.е. таблица умножения, то получится астрономическая цифра. Ни одно имя ученого не повторяется так часто.
Слайд 5.

Пифагор был создателем научно-философской школы, ставшей действительно союзом Истины, Добра и Красоты. Он был властителем дум, философом, которого по силе духа и силе воздействия сравнивают с его великими современниками: Конфуцием, Буддой и Заратуштрой. Пифагор 2500 лет назад направил людей по пути торжества Разума. Он воспитал веру в могущество разума, убежденность в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.
Идеи пифагорейского учения в арифметике, геометрии, космологии, музыке повлияли на развитие человечества.
Слайд 6.
В
 своих гипотезах пифагорейцы исходили из одной глобальной идеи: гармонического устройства мироздания. Вот почему Вселенную, по преданию, впервые Пифагор назвал словом «космос», которое первоначально обозначало у греков порядок, надлежащую меру, прекрасное устройство. Тем самым великий мыслитель хотел подчеркнуть важнейшие свойства мироздания – его упорядоченность, организованность, симметрию, а значит, и красоту.
своих гипотезах пифагорейцы исходили из одной глобальной идеи: гармонического устройства мироздания. Вот почему Вселенную, по преданию, впервые Пифагор назвал словом «космос», которое первоначально обозначало у греков порядок, надлежащую меру, прекрасное устройство. Тем самым великий мыслитель хотел подчеркнуть важнейшие свойства мироздания – его упорядоченность, организованность, симметрию, а значит, и красоту. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер» впервые появились именно в Школе Пифагора.
Согласно учению пифагорейцев, числа предшествуют гармонии, так как их неизменные законы управляют всеми гармоническими пропорциями.
Для Пифагора музыка была производной от божественной науки математики, и ее гармонии жестко контролировались математическими пропорциями.
Ученый занимался экспериментами, с помощью чаши с водой и однострунной арфы пытаясь найти соотношения между высотой музыкального тона и числами.
Слайд 7.
Поискам гармонических отношений в космосе посвящена одна из глав книги Кеплера «Гармония мира» (1619). По прошествии 2000 лет после Пифагора музыка сфер вновь зазвучала в астрономических открытиях Кеплера, а через 300 лет после Кеплера та же гармония целочисленных отношений была обнаружена в микрокосмосе атома. «Музыкальное строение» микрокосмоса, открытое квантовой механикой XX века, было угадано пифагорейцами 2500 лет назад. За огромный промежуток времени, наука совершила два гигантских витка по спирали, в каждом из которых старый пифагорейский мотив о всеобщей гармонии звучал в хоре самых современных научных знаний.
К
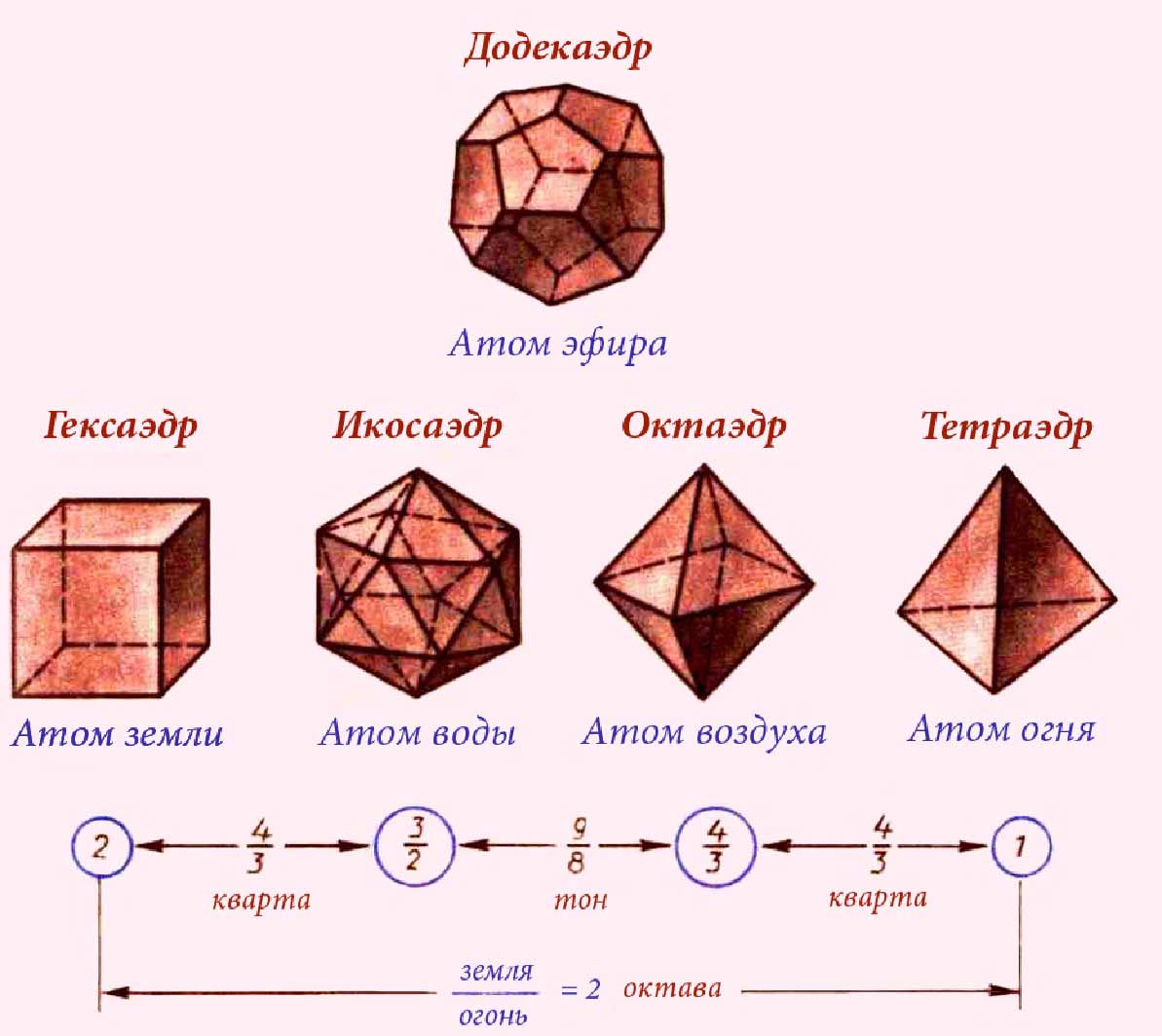 ак же был устроен микрокосмос пифагорейцев?
ак же был устроен микрокосмос пифагорейцев? Согласно некоторым источникам, четыре элемента, первоосновы материального мира - огонь, воздух, земля и вода – были геометризированы самим Пифагором. Атом каждой стихии мыслился в виде определенного правильного многогранника. Эту идею развил Платон, именно от него мы знаем о пифагорейском микрокосмосе.
Согласно пифагорейско-платоновской теории, атомам земли придавалась форма куба, т.к. и земля, и куб отличаются неподвижностью, устойчивостью. Атомам воды – форма икосаэдра, ибо вода отличается текучестью, а из всех правильных тел икосаэдр – наиболее «катящийся». Атомам воздуха - форма октаэдра, поскольку воздух движется взад и вперед, а октаэдр как бы направлен одновременно в разные стороны. Атомам огня – форма тетраэдра, как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник – додекаэдр. Для него Платон вводит пятый элемент - мировой эфир, атомам которого придается форма додекаэдра, как наиболее близкого к шару – самому совершенному по форме телу. С тех пор правильные многогранники называются также «платоновскими телами».
Слайд 8.

Конечно, пифагорейско-платоновская теория пяти стихий мироздания вызывает сегодня лишь вежливую улыбку. Но какова же внутренняя мудрость, которая вела древних к их отжившему учению? А такая мудрость в пифагорейско-платоновской теории есть. Более того, она оказывается удивительно современной.
Сегодняшнее мироздание объемлет не пять стихий, а более ста атомов элементов, но, как и 2500 лет назад, это число ничтожно в сравнении с огромным разнообразием рождаемых ими веществ.
Слайд 9.
Сверхзадача современной физики – выявление истинных «кирпичиков» Мироздания – элементарных частиц – первичных, неразложимых далее элементов, из которых состоит вся материя. Еще в начале XX века считалось, что таких частиц три: электрон, протон и нейтрон. Однако катастрофический рост числа открываемых элементарных частиц привел во второй половине XX века к пересмотру воззрений об их элементарности. Сегодня есть основания считать, что такие «экс-элементарные» частицы, как протоны, нейтроны, мезоны, гипероны и др. состоят из различных комбинаций трех типов кварков (либо пар кварк-антикварк) – самых современных первооснов Мироздания.
III. Фундамент науки геометрии: теоретические основы
Слайд 10.
Мы только что говорили о «кирпичиках» Мироздания. А из каких «кирпичиков» складывается наука геометрия у Евклида? Что составляет фундамент науки. Если ее образно представить в виде дома?
Н
 аука опирается на основные понятия, которым мы не даем определения. Это точка, прямая, плоскость, расстояние, множество.
аука опирается на основные понятия, которым мы не даем определения. Это точка, прямая, плоскость, расстояние, множество. (Хотя «точка» - абстрактное понятие. Точка – след карандаша на бумаге, самолет в небе, звезда и т.д. Мы также не даем определения прямой, плоскости, но представляем их бесконечность.)
С помощью этих понятий мы даем определения. Вспомните определение отрезка (часть прямой, ограниченная двумя точками). Какие основные понятия используются в этом определении? (точка, прямая)
Вспомните аксиому прямой. (Через две точки можно провести прямую, и притом только одну.)
Что называется аксиомой? Теоремой?
Аксиома в переводе на русский язык означает положение, достойное уважения, бесспорное утверждение.
То есть аксиомой мы называем некоторое утверждение о свойствах геометрических фигур, принимаемое истинным без доказательств в качестве исходного.
Но основе аксиом доказываются далее теоремы, строится вся геометрия.
IV. Актуализация знаний учащихся по программе 7 класса. Блиц-опрос
Слайд 11.
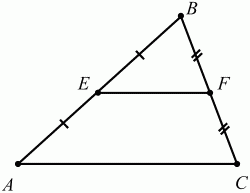
Сформулируйте теоретические положения, которые соответствуют следующим рисункам. Запишите в тетрадь план ответов по каждому рисунку, можете обсудить рисунки в парах (5 мин.).
1
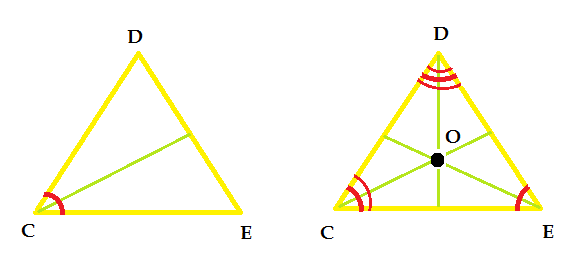 ).
).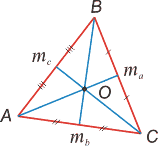
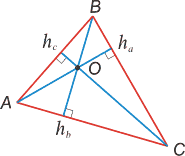
(По рисунку учащиеся дают определения медианы, биссектрисы, высоты треугольника.)
Слайд 12.
2).
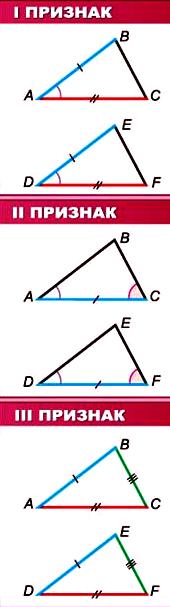


(По рисунку учащиеся формулируют признаки равенства треугольников.)
Слайд 13.