Пример 2. Моделирование временного отклика динамических систем


Постановка задачи

Определить временные характеристики звена (переходную и весовую характеристики) на примере колебательного звена второго порядка
. (3.1)

Решение.

Для построения схемы моделирования воспользуемся методом понижения производной (методом Кельвина). В нем можно выделить следующие этапы.

• 
  Разрешаем уравнение относительно старшей производной
  

. (3.2)

• 
  Полагаем старшую производную известной и выполняем ее последовательное интегрирование, получая все низшие производные и саму переменную y. Для этого потребуется два последовательно включенных интегратора, на выходах которых получим сигналы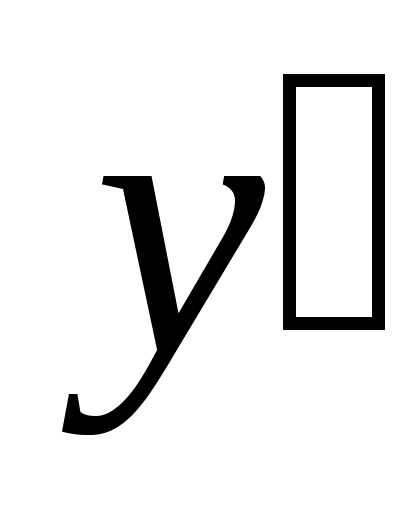 и y.
  
• 
  Формируем старшую производную, используя уравнение (3.2). Для этого потребуется сумматор, складывающий сигналы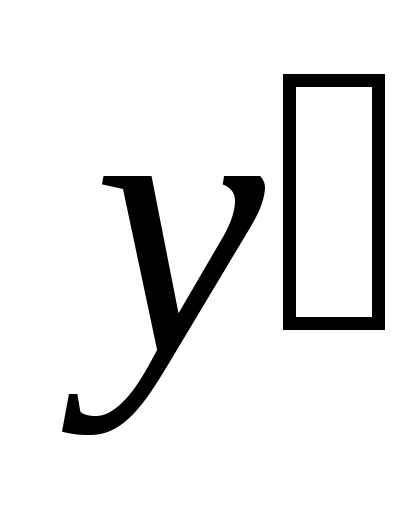 и y, умноженные, соответственно, на коэффициенты -0,167 и -0,333.
  
• 
  Для получения переходной и весовой характеристик на один из входов сумматора подаем единичный сигнал .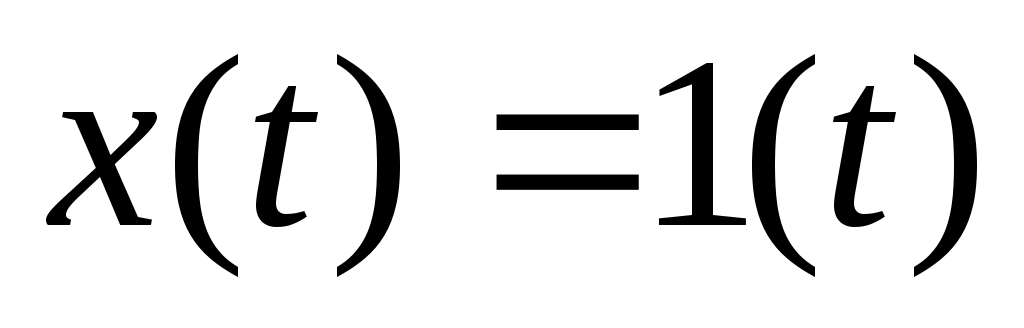
  
• 
  Запускаем систему Matlab, а затем систему Simulink (см. п. 3.3).
  

Создаем окно новой модели File→New→Model.

• 
  С помощью имеющихся блоков системы Simulinkсобираем структурную схему (рис.3.4).
  

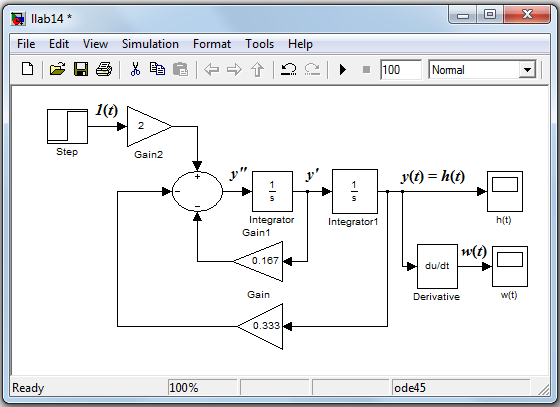
Рис.3.4. Схема моделирования для снятия временных характеристик

Для сбора модели используются следующие блоки библиотеки Simulink:

• 
  ступенчатая функция – библиотека Sources → Step;
  
• 
  линейные преобразователи – библиотека Commonly Used Bloks → Gain;
  
• 
  интеграторы – библиотека Continuous → Integrator;
  
• 
  сумматор – библиотека →CommonlyUsedBloks → Sum;
  
• 
  виртуальные осциллографы – библиотека Sinks → Skope;
  
• 
  производная - библиотека Continuous → Derivative.
  

Параметры ступенчатого входного сигнала задаются в блоке

---

Step (рис.3.5). Для проведения расчетов амплитуду входного сигнала зададим равной единице.


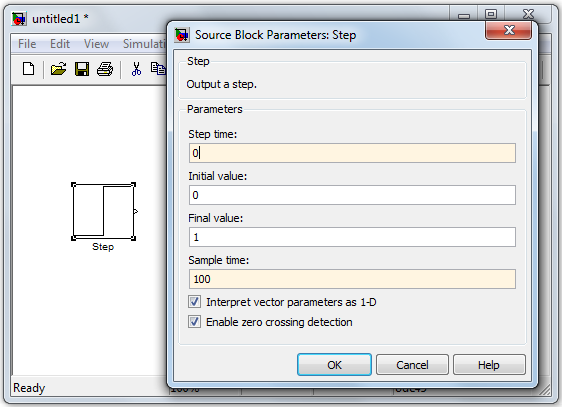
Рис.3.5.

Для расчета модели необходимо выбрать пункт меню Simulation/Start или инструмент на панели инструментов.

Для просмотра результатов моделирования нужно дважды щелкнуть левой кнопкой мыши по блоку Scope.

При необходимости можно увеличить время расчета Stoptime, с 10 с. По умолчанию, до, например, 100 с. Этот параметр задается в окне Simulation/Configuration Parameters. Время расчета задается указанием начального (Start time) и конечного (Stop time) значений времени расчета. Начальное время, как правило, задается равным нулю. Величина конечного времени задается пользователем исходя из условий решаемой задачи.

После повтора расчета результат выглядит, как показано на рис.3.6.


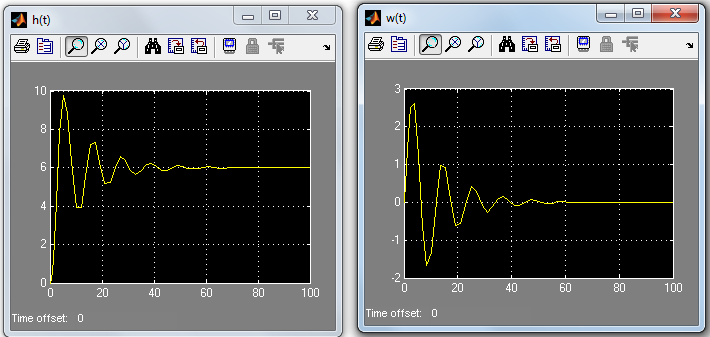
Рис.3.6. Переходная и весовая характеристики соответственно
Пример 3. Моделирование частотного отклика динамических систем

Постановка задачи

Построить ЛАЧХ (линейную амплитудно-частотную характеристику) и ЛФЧХ (линейную фазово-частотную характеристику) звена, заданного с помощью передаточной функции

.
Решение (Вариант 1)

Схема для снятия частотных характеристик в системе Simulink изображена на рис.3.7.


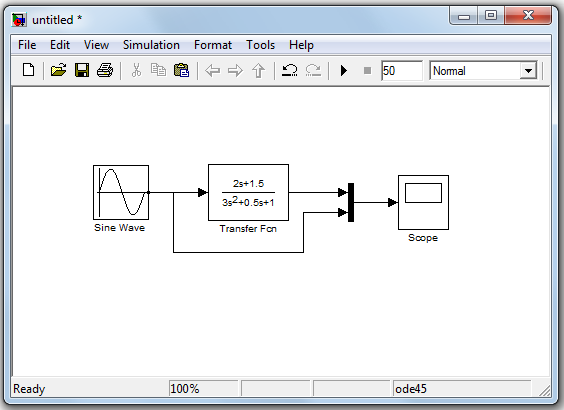
Рис.3.7. Первый вариант схемы моделирования для снятия частотных характеристик
Для сбора модели используются следующие блоки библиотеки Simulink:

• 
  синусоидальный сигнал – библиотека Sources → SineWave;
  
• 
  динамическое звено – библиотека Continuous → TransferFcn;
  
• 
  мультиплексор – библиотека CommonlyUsedBloks→Mux;
  
• 
  виртуальные осциллографы – библиотека Sinks → Skope.
  

Параметры входного гармонического сигнала: амплитуда - и угловая частота

---

задаются в блоке SineWave. Для расчетов амплитуду входного сигнала задаем равной единице.

Блок Mux предназначен для одновременного наблюдения на осциллографе входного и выходного сигналов.

Результат моделирования при представлен на рис.3.8.


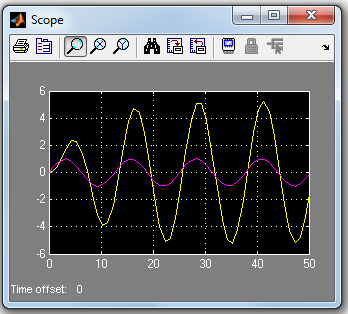
Рис. 3.8. Входной сигнал (розовая линия) и отклик системы (желтая линия)
На экране виртуального осциллографа в общем случае будет наблюдаться изображение (рис.3.9)

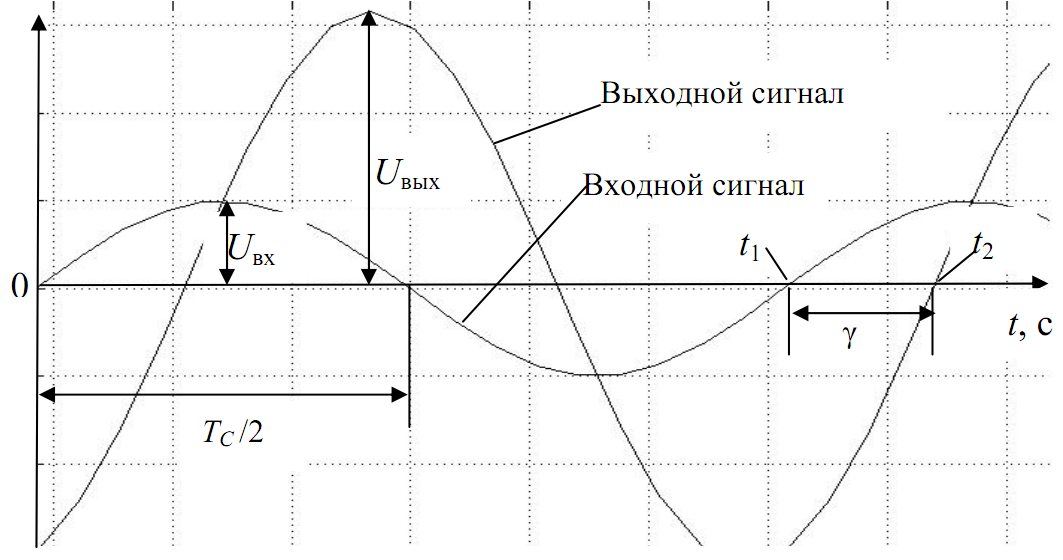
Рис.3.9

Решение (Вариант 2)

Для получения динамических характеристик системы (рис.3.8) можно воспользоваться функциями Linear Analysisпакета расширения Control System Toolbox. Для этого необходимо выставить метку Input Point щелкнув правой кнопкой мыши по стрелке перед блоком Transfer Fcn и набрать LinearizationPoints / InputPoint. Аналогично выставляется метка OutputPoint (рис.3.10).


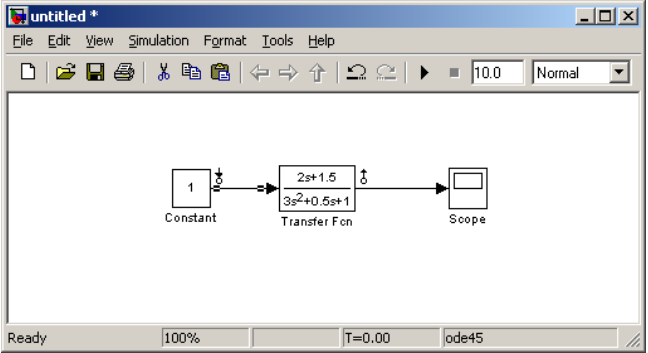
Рис.3.10. Второй вариант схемы моделирования для снятия частотных характеристик

Далее, набрав команду Tools / Control Design / Linear Analysis, открывается окно Control and Estimation Tools Manager

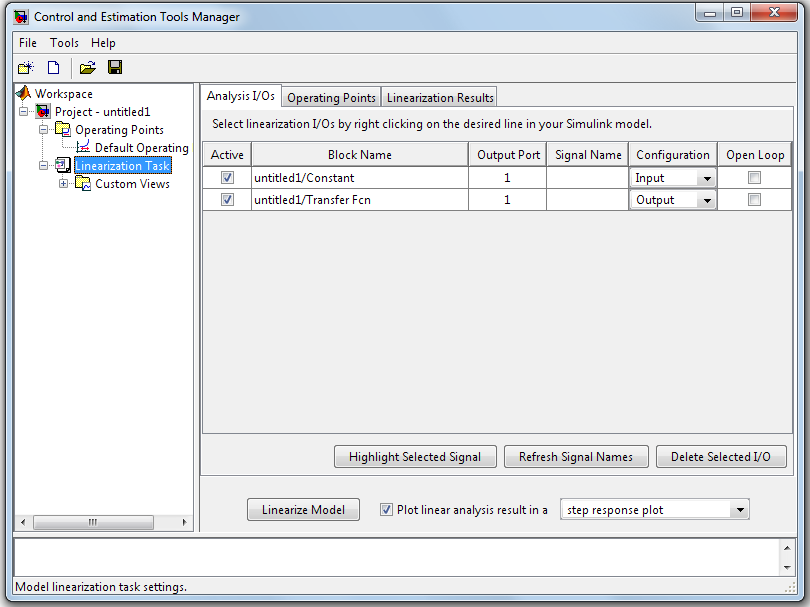
Рис. 3.11
Здесь обозначены расставленные на модели точки. Здесь можно поменять входы и выходы, а также деактивировать некоторые точки.

Далее нажимаем на кнопку LinearizeModel и получаем окно с графическим отображением динамических характеристик (рис.3.12).


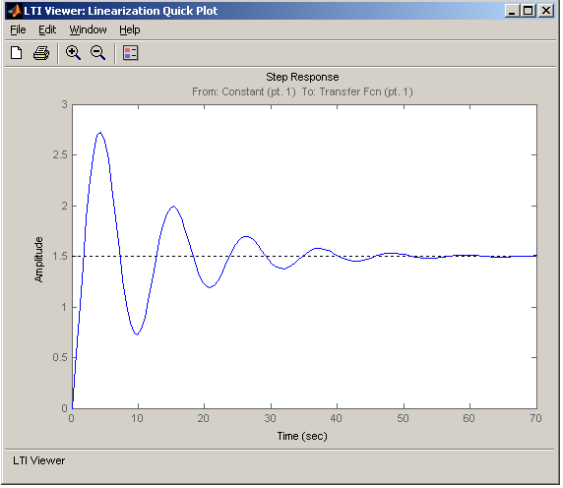
Рис.3.12 Переходной процесс
Для переключения между графиками нужно щелкнуть правой кнопкой мыши по графику и выбрать из подменю PlotTypes/«необходимый график». Здесь «необходимый график» - одина из диграмм:

• 
  Step – реакция на единичный скачок;
  
• 
  Impulse – импульсная характеристика;
  
• 
  Bode, Bode Magnitude – диаграммы Боде;
  
• 
  Nyquist – диаграмма Найквиста;
  
• 
  Nichols - диаграмма Никольса (логарифмическая амплитудно-фазовая диаграмма);
  
• 
  Pole/Zero – картанулей и полюсов.
  

---

На рис.3.13 - 3.14 в качестве примера изображены диаграммы Найквиста и Боде.

Диаграмма Найквиста строится в системе координат: по оси абсцисс откладывается действительная часть передаточной функции при , по ординат – мнимая. Для получения годографа осуществляется изменение частоты от 0 до ∞.


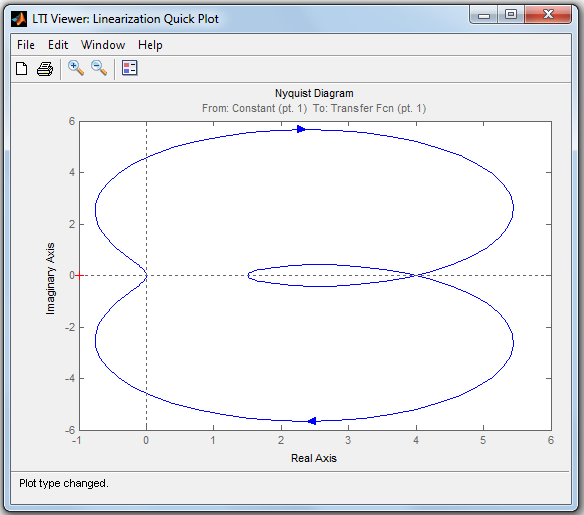
Рис.3.13. Фазовый портрет – диаграмма Найквиста


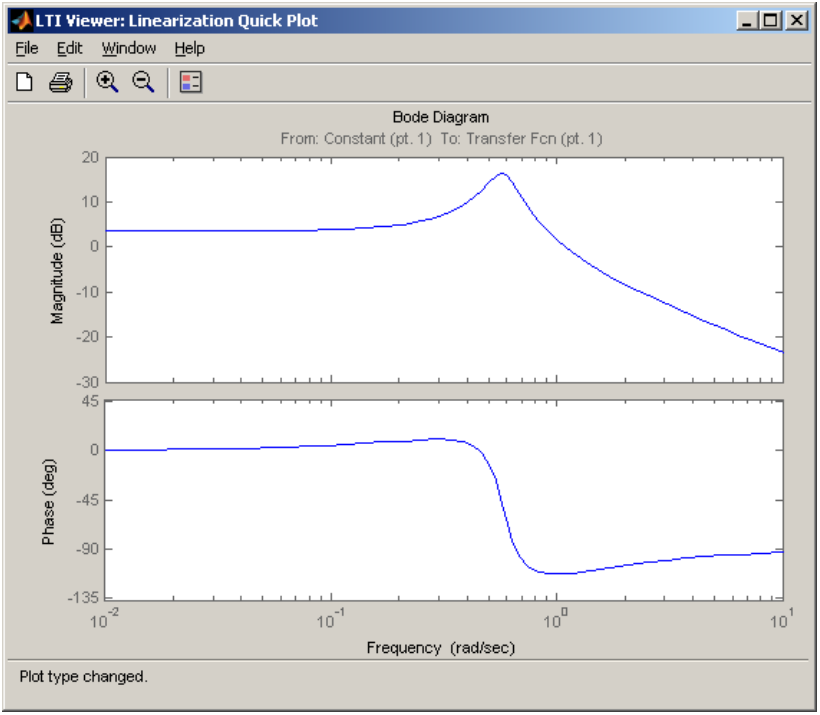
Рис.3.14. Частотная характеристика – диаграмма Боде

Пример 4. Анализ динамических свойств на основе

дифференциальной модели

Постановка задачи

Исследовать математическую систему, показанную на рис. 3.1


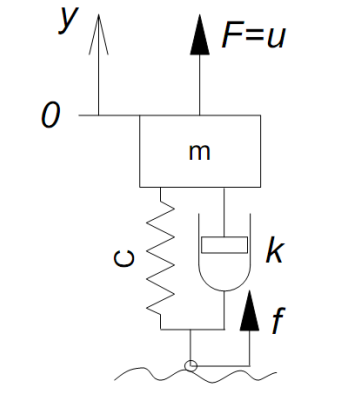
Рис. 3.15. Модель системы подрессоривания:

- силовое воздействие;

- кинематическое воздействие.
и исследовать ее при заданных числовых значениях параметров



Здесь и - амплитуды кинематического и силового воздействий соответственно.

Решение

Система описывается дифференциальным уравнением второго порядка

. (3.1)

Преобразуем уравнение к виду, необходимому для моделирования в среде Matlab Simulink

. (3.2)

Схема для решения дифференциального уравнения представлена на рис. 3.2.

Построение модели начинаем с сумматора. К выходу сумматора подключается линейный преобразователь (множитель 1/m), на выходе которого получаем значение второй производной. Далее подключаем два интегратора, на выходе которых получаем значение первой производной и самой функции.

Далее устанавливаем связи между входами и выходами соответствующих блоков, применяя, где необходимо, дополнительные преобразователи и сумматоры).

---

Для вычисления производной кинематического воздействия используется блок дифференцирования.



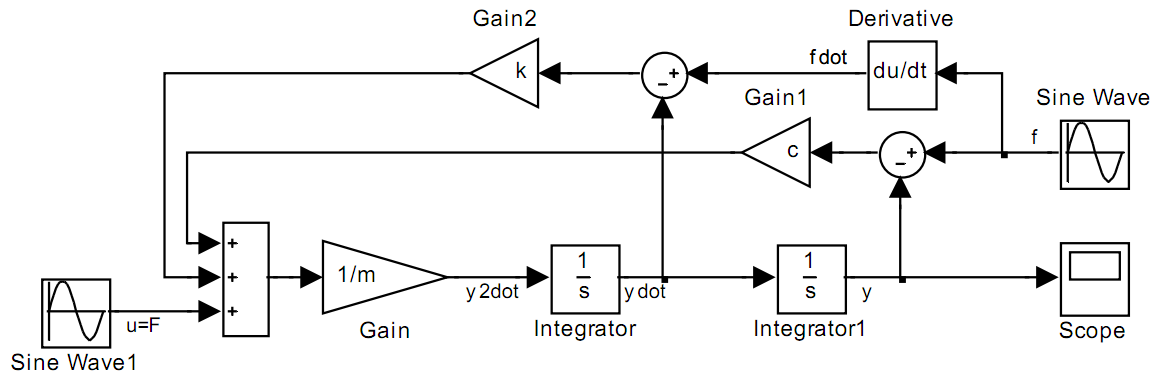
Рис.3.16. Схема Matlab Simulink для решения уравнения (3.2)
3.3. Принципы функционирования среды matlab и simulink
3.3.1. Общие сведения
Система Simulink является составной частью системы MATLAB, предназначенной для структурно-графического моделирования различных динамических объектов, как непрерывных, так и дискретных. В данном методе объект представляется в виде совокупности готовых, законченных блоков, между которыми устанавливаются связи по типу «вход-выход». В графике модели такие связи изображаются простыми стрелками.

Пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты. Это чрезвычайно упрощает процесс моделирования, делает его высокоэффективным.
Для запуска программы необходимо предварительно запустить пакет MATLAB. Основное окно пакета MATLAB показано на рис.3.17. Там же показана подсказка появляющаяся в окне при наведении указателя мыши на ярлык Simulink в панели инструментов.


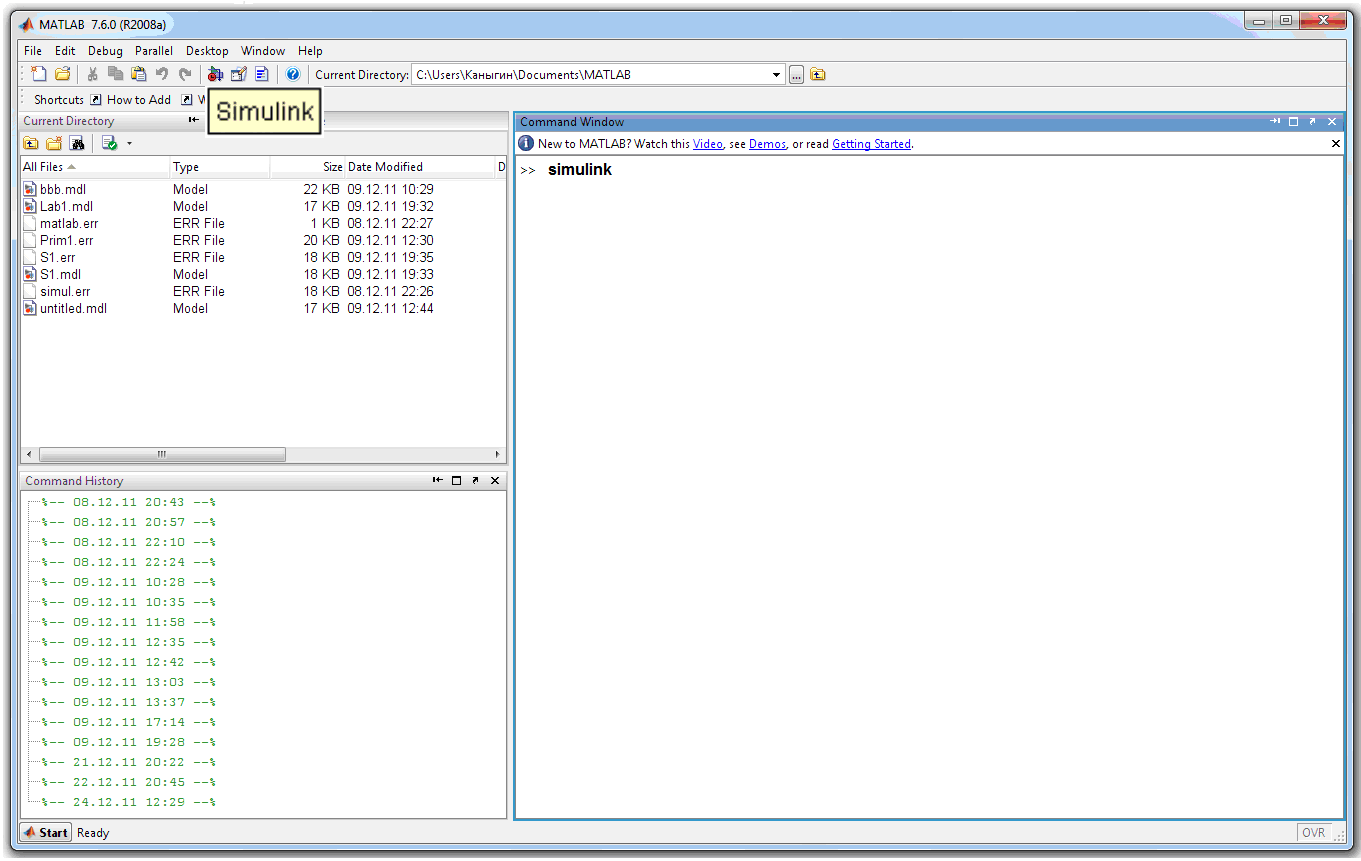
Рис 3.17. Основное окно программы MATLAB
После открытия основного окна программы MATLAB нужно запустить

программу Simulink. Это можно сделать одним из трех способов:

• 
  Нажать кнопку (Simulink) на панели инструментов командного окна
  

MATLAB.

• 
  В командной строке (после символа >>) главного окна MATLAB напечатать Simulink и нажать клавишу Enter на клавиатуре.
  
• 
  Выполнить команду Open… в меню File и открыть файл модели (mdl -
  

файл).

Последний вариант удобно использовать для запуска уже готовой и отлаженной модели, когда требуется лишь провести расчеты и не нужно добавлять новые блоки в модель. Использование первого и второго способов приводит к открытию окна браузера разделов библиотеки Simulink (рис. 3.18).


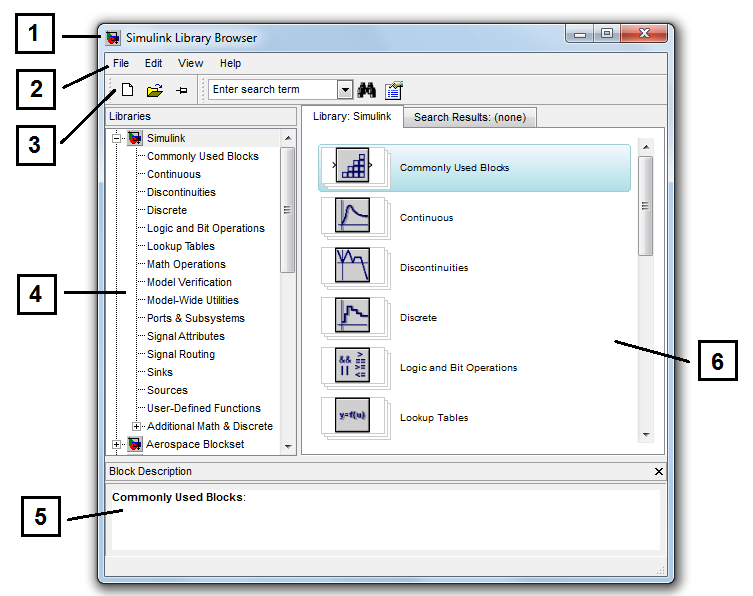
Рис. 3.18. Окно браузера (обозревателя) библиотеки Simulink
Обозреватель разделов библиотеки Simulink

---

Смотрите также файлы

• Спорные проблемы великой отечественной войны.docx

• 2. раздел расчетные элементы.docx

• Кабир (1440, Varanasi, Jaunpur, India 1518, Maghar) Грантхавали (Собрание).doc

• Методы обследования пациентов с инфекционными заболеваниями в сестринской практике.docx

• Отправления передал (Отправитель) ( ) (подпись) (расшифровка).pdf