Вариант 14

По заданной схеме построить имитационную модель и провести моделирование для 20000 заявок.



В СМО поступает поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 6 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 40 до 44 секунд со средним значением 42 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 3 до 9 секунд со средним значением 6 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе.

Вариант 15

По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.


Количество заявок в системе фиксировано и равно 10, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по экспоненциальному закону со средним значением 20 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 23 до 29 минут со средним значением 26 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q.

Вариант 16

По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.



Количество заявок в системе фиксировано и равно 7, они поступают в нее сразу после начала моделирования. Система работает без отказов. Время обработки в D1 величина случайная, распределенная по равномерному закону в интервале от 10 до 16 минут со средним значением 13 минут. Длительность перехода заявки из D1 в Q2 величина случайная, распределенная по равномерному закону в интервале от 32 до 40 минут со средним значением 36 минут. Время обработки в D2 величина случайная, распределенная по экспоненциальному закону со средним значением 15 минут. Длительность перехода заявки из D2 в Q1 величина случайная, распределенная по равномерному закону в интервале от 28 до 30 минут со средним значением 27 минут. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q1 и Q2.

---

Вариант 17

По заданной схеме построить имитационную модель и провести моделирование для 30000 заявок.



В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 13 секунд. Заявки выбираются на обслуживание из накопителя ограниченной емкости равной 8 в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 40 до 46 секунд со средним значением 43 секунд. В отчете отобразить обслуженные и не обслуженные заявки, данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе.

Вариант 18

По заданной схеме построить имитационную модель и провести моделирование для 15000 заявок.



В СМО поступают два класса заявок, заявки первого класса S1 интервалы между которыми распределены по экспоненциальному закону со средним значением 12 секунд и заявки второго класса S2 интервалы между которыми распределены по равномерному закону в интервале от 18 до 26 секунд со средним значением 22 секунды. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления. В системе 4 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе для заявок первого класса постоянна и равна 24 секундам, для заявок второго класса распределена по экспоненциальному закону со средним значением 20 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе.

---

Вариант 19

По заданной схеме построить имитационную модель и провести моделирование для 30000 заявок.



В СМО поступает поток заявок, интервалы между которыми равномерно в интервале от 10 до 14 секунд со средним значением 12 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости Q1 в порядке поступления. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по равномерному закону в интервале от 38 до 46 секунд со средним значением 42 секунд. Очередь Q2 также неограниченной емкости. Длительность обслуживания в приборе D1 распределена по равномерному закону в интервале от 4 до 10 секунд со средним значением 8 секунд. В отчете отобразить данные по МКУ и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очередях и плотности распределения времени пребывания заявок в системе.

Вариант 20

По заданной схеме построить имитационную модель и провести моделирование в течение 8 часов.



Количество заявок в системе фиксировано и равно 18, они поступают в нее сразу после начала моделирования. Система работает без отказов. В системе 5 идентичных обслуживающих приборов D. Длительность обслуживания в одном приборе распределена по экспоненциальному закону со средним значением 18 минуты. Длительность перехода заявки из D в Q величина случайная, распределенная по равномерному закону в интервале от 20 до 30 минут со средним значением 25 минут. В отчете отобразить данные по МКУ и очередям, а так же построить гистограмму плотности распределения времени ожидания заявок в очереди Q.
2. Примеры выполнения лабораторной работы

Пример 1. «Одноканальное устройство»

По заданной схеме построить имитационную модель и провести моделирование для 10000 заявок.



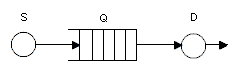
где S – источник заявок, Q – очередь, D – обрабатывающее устройство(канал обслуживания).

В СМО поступает простейший поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд. Заявки выбираются на обслуживание из накопителя неограниченной емкости в порядке поступления.

---

Длительность обслуживания заявок в устройстве – величина случайная, распределенная по равномерному закону в интервале от 4 до 12 секунд со средним значением 8 секунд. В отчете отобразить данные по каналам обслуживания и очередям, а так же построить гистограммы плотности распределения времени ожидания заявок в очереди и плотности распределения времени пребывания заявок в системе.
tabl_1 QTABLE ocher,5,10,10; таблица для гистограммы плотности распределения времени ожидания заявок в очереди

tabl_2 TABLE M1,10,10,10; таблица для гистограммы плотности распределения времени пребывания заявок в системе

GENERATE (EXPONENTIAL(5,0,10)) ; формирование потока заявок

QUEUE ocher; отметка момента поступления заявки в очередь

SEIZE kan; занятия прибора с именем kan

DEPART ocher; отметка момента покидания заявкой очереди

ADVANCE 8,4; задержка на время 8±4 единицы времени

RELEASE kan; освобождение прибора с именем kan

TABULATE tabl_2; регистрирует время покидания заявкой системы

TERMINATE 1; удаление заявки из модели

START 10000
Рассмотрим подробно представленную модель и прокомментируем каждый оператор GPSS-модели, сопоставив их с реально протекающими в системе процессами.
Первыйоператор (команда) QTABLE формирует таблицу для гистограммы плотности распределения времени ожидания заявок в очереди, имя которой указано в операнде A.

Имя tabl_1 задаёт имя таблицы (гистограммы), а операнды A, B, C и D задают соответственно:

A=ocher – имя очереди, для которой формируется гистограмма;

B=5 – верхнюю (правую) границу первого частотного интервала гистограммы;

C=10 – величину всех остальных частотных интервалов;

D=10 – количество частотных интервалов.

Второйоператор TABLE формирует таблицу для гистограммы плотности распределения времени пребывания заявок в системе.

Имя tabl_2, как и в предыдущем случае, задает имя таблицы(гистограммы), а операнды A, B, C и D задают соответственно:

A=M1 – величину, для которой формируется гистограмма; в нашем примере M1 представляет собой СЧА, определяющее резидентное время, вычисляемое как разность между текущим значением модельного времени, определяемым в момент вхождения транзакта в блок TABULATE, и временем появления транзакта в модели, то есть временем поступления заявки в систему, являющимся одним из параметров транзакта;

B=10 – верхнюю границу первого частотного интервала;

---

C=10 – величину всех остальных частотных интервалов;

D=10 – количество частотных интервалов.

Таким образом, команда TABLE используется совместно с блоком TABULATE, который регистрирует момент прохождения транзактом (заявкой) определенного места в модели. Соответственно блок TABULATE должен находиться в модели в том месте, относительно которого измеряется искомое время. Таким местом при измерении времени пребывания заявки в моделируемой системе является точка выхода заявки из системы, когда транзакт покидает прибор многоканальной системы. В качестве параметра A оператора TABULATE выступает имя соответствующей таблицы (гистограммы). В нашем случае эта таблица и соответствующая ей гистограмма имеет имя tabl_2.

Оператор TABLE так же, как и QTABLE, позволяет сформировать гистограмму плотности распределения случайной величины и имеет аналогичную структуру. Основное отличие TABLE от QTABLE состоит в том, что оператор TABLE позволяет формировать гистограмму плотности распределения случайной величины между двумя, в общем случае, произвольными моментами времени, в то время как QTABLE всегда формирует гистограмму плотности распределения времени ожидания в очереди.

Оператор GENERATE формирует поток заявок, интервалы между которыми распределены по экспоненциальному закону со средним значением 10 секунд.

Когда модельное время становится равным моменту формирования очередного транзакта, последний начинает движение в модели к следующему по порядку оператору QUEUE, который заносит транзакт (заявку) в очередь с именем «ocher».

Далее транзакт продолжает движение к следующему оператору SEIZE, в соответствии с которым выполняет попытку занять одноканальное устройство (прибор) с именем «kan». При этом проверяется занятость устройства. Если прибор занят обслуживанием ранее поступившего транзакта, то рассматриваемый транзакт приостанавливает свое движение и остается в очереди до тех пор, пока не освободится прибор. Если прибор свободен, то рассматриваемый транзакт продвигается к следующему оператору DEPART.

Оператор DEPART отмечает момент покидания транзактом очереди с именем (номером) «ocher» с целью сбора статистики по очередям (определяется время нахождения транзакта в очереди, то есть время ожидания заявки). Двигаясь дальше, транзакт попадает в оператор ADVANCE.

---

Смотрите также файлы

• Аымды баылау 3 Таырып. Топыра ортасы жадайыны биоиндикациясы.docx

• Отчёт по практической работе 4.docx

• 6А Сынып азастан тарихы. Iнса 1Тапсырма.docx

• Пп Наименования теоретических и практических педагогических дисциплин.docx

• Лабораторная работа 2 Динамические системы и методы их математического.doc