Файл: Отчет по лабораторной работе 10 по дисциплине Математическое и имитационное моделирование экономических процессов.docx
Добавлен: 09.01.2024
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра автоматизированных систем управления (АСУ)
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. БИРЖЕВОЙ ИГРОК
Отчет по лабораторной работе №10
по дисциплине «Математическое и имитационное моделирование экономических процессов»
| | Выполнили: студенты гр. 440-1 |
| | _________ Заигрин Д.Ю. |
| | _________ Верповский С.В. |
| | «___» _____________ 2023 г. |
| | Руководитель: |
| | профессор, д.т.н. |
| | _________ Мицель А.А. |
| | «___» _____________ 2023 г. |
Томск 2023
ТЕОРИЯ
1.1 Описание модели
Биржевой игрок разработал свой порядок приобретения и продажи акций, состоящий в следующем:
1) обладая пакетом акций, необходимо продать его, как только цены на эти акции начинают падать;
2) как только цены на акции начинают возрастать, их необходимо покупать.
Игрок не желает рисковать своими ограниченными средствами в натурном эксперименте и хочет оценить прибыльность своей стратегии с помощью имитационного моделирования. Для упрощения дальнейших рассуждений будем предполагать, что:
а) игрок покупает и продает только одни какие-нибудь акции;
б) в рассматриваемый момент времени, принимаемый за начальный, игрок располагает пакетом в 100 акций, стоимостью в 10 денежных единиц каждая, и цена акции может ежедневно изменяться на 1 денежную единицу (если сегодня акция стоит 10 денежных единиц, то завтра она будет стоить 9, 10 или 11 денежных единиц);
в) игрок совершает не более одной сделки в день и за каждую сделку платит комиссионные в размере 2 % стоимости купленных или проданных акций;
г) игрок не располагает иными средствами, кроме пакета в 100 акций.
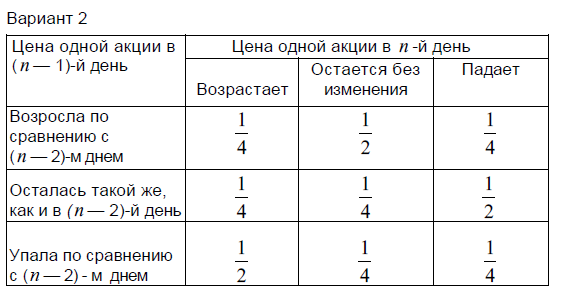
Для оценки прибыльности своей стратегии игрок построил модель суточных флуктуации цен на акции с использованием ретроспективных биржевых данных. Эта модель представлена в виде табл. 1 и определяет вероятности изменения цен на акции. Согласно этой модели, если в понедельник и во вторник цена одной акции равнялась 10 денежным единицам, то в среду (см. табл. 1, вторая строка снизу) она будет стоить 11 денежных единиц с вероятностью 1/4, 10 денежных единиц с вероятностью 1/2 и 9 денежных единиц с вероятностью 1/4. Если же во вторник цена одной акции равнялась 9 денежным единицам, то в среду (см. табл. 1, первая строка снизу) она будет стоить 10 денежных единиц с вероятностью 1/4, 9 денежных единиц с вероятностью 1/4 и 8 денежных единиц с вероятностью 1/2.
Таблица 1
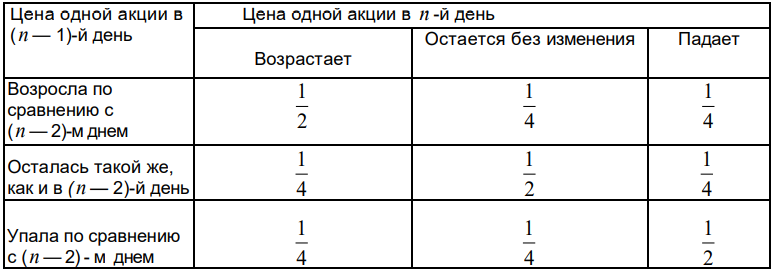
Прежде чем начинать процесс имитационного моделирования, необходима генерация случайных событий, которые с соответствующими вероятностями их реализаций представлены в табл. 1. Не располагая ни вычислительной техникой, ни соответствующим программным обеспечением, наш игрок решил воспользоваться простейшим способом, который заключается в бросании двух монет. Соответствие между возможными исходами этого случайного испытания и генерируемыми случайными событиями он отразил в табл. 2.
Таблица 2
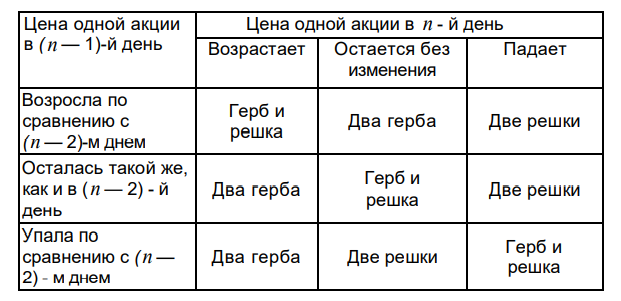
1.2 Прогон модели
Предположим, что игрок решил ограничить длительность периода имитации 20 днями и каждому дню поставил в соответствие номер k = 1, 20. Эти номера, расположенные в порядке возрастания, образуют столбец 1 в табл. 3, отражающей результаты имитирования изменения цен на акции. Столбец 2 в табл. 3 он заполнил после 20-кратного подбрасывания двух монет, воспользовавшись следующими обозначениями: ГГ -— выпали два герба; ГР — выпали один герб и одна решка; РР — выпали две решки. Для определения изменения цен на акции необходимо задать начальные условия: цену одной акции в день с номером k = 0 и направление изменения вчерашней цены. В соответствии с исходными предположениями начальная цена одной акции равнялась 10 денежным единицам и совпадала с ценой в предшествующий день. Это нашло свое отражение в первой строке столбца 3 табл. 3, в котором игрок фиксировал направления изменения вчерашней цены акции. В столбце IV он фиксировал сегодняшнюю цену одной акции.
Таблица 3
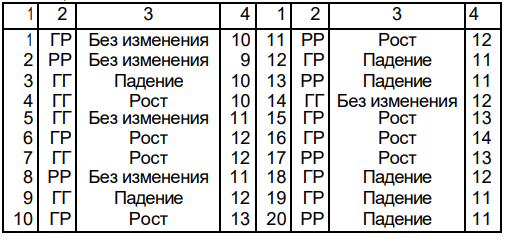
Согласно табл. 2, при рассматриваемых начальных условиях выпадение герба и решки при первом бросании двух монет означает, что в первый день цена акции не изменяется (первая строка, столбец 3) и остается равной 10 денежным единицам (первая строка, столбец 4). Поскольку цены акций в первый день имитирования равны 10 денежным единицам, то выпадение двух решек при втором бросании двух монет (вторая строка, столбец 2) означает падение цены до 9 денежных единиц за акцию (вторая строка, столбец 4). Аналогично проверяется правильность заполнения игроком двух последних столбцов табл. 3.
1.3. Результаты моделирования
Воспользовавшись данными об изменении цены акции за двадцатидневный период, представленными в табл. 3, наш игрок составил табл. 4, в которой отразил результаты имитационного моделирования своей стратегии купли и продажи акций на бирже. Прочерки в третьем столбце этой таблицы означают отсутствие сделок, что может быть обусловлено как выбранной стратегией поведения игрока (дни имитации 1, 4, 7, 13, 20), так и отсутствием у него либо наличных денег (дни имитации 5, 6, 10, 15, 16), либо акций (дни имитации 12, 18, 19). При определении наличных денег учитывались комиссионные с каждой сделки. Так, например, на девятый день имитации игрок, располагая наличностью в размере 931,88 денежных единиц, купил 76 акций по цене 12 денежных единиц за акцию, заплатил комиссионные в размере 0,02 • 12 • 76 = 18,24 денежных единиц и у него осталось в наличии 931,88 — 12 • 76 — 0.02 • 12 • 76 = 1,64 денежных единиц.
Проанализировав результаты имитационного моделирования, записанные в табл. 4, можно сразу отметить, что, придерживаясь своей стратегии, биржевой игрок останется в проигрыше. Но это лишь первое впечатление. Действительно, если процесс имитирования оборвать на шестой или шестнадцатый день, то он выиграет. А что будет, если повторить имитационный эксперимент или увеличить длительность периода имитирования?
Даже этот простейший пример имитационного моделирования игры на фондовой бирже порождает ряд весьма сложных вопросов относительно меры эффективности выбираемой стратегии и метода проектирования научно обоснованного эксперимента по проверке этой эффективности. Кроме того,
становится очевидным, что, несмотря на простоту вычислительных процедур при имитационном моделировании, их объем весьма значителен. Поэтому конструктивное использование имитационного моделирования практически невозможно без использования быстродействующей вычислительной техники.
Таблица 4
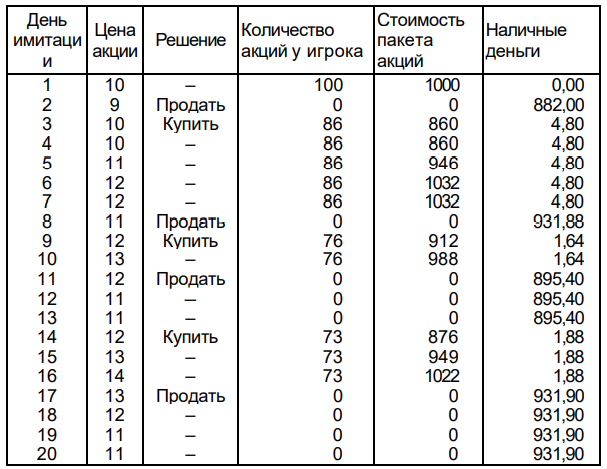
2 РЕЗУЛЬТАТ
Задание
1. Выполнить имитационное моделирование биржевой игры с помощью равномерного датчика случайных чисел, распределенных в интервале (0,1).
2. Проанализировать результаты моделирования для 20 дней:
а) для одной реализации случайных чисел;
б) для 10 реализаций случайных чисел
3. Написать программу в пакете Mathcad.
Вариант 2:
Решение:

Рисунок 1 – Решение задания, часть 1

Рисунок 2 – Решение задания 2 пункт а
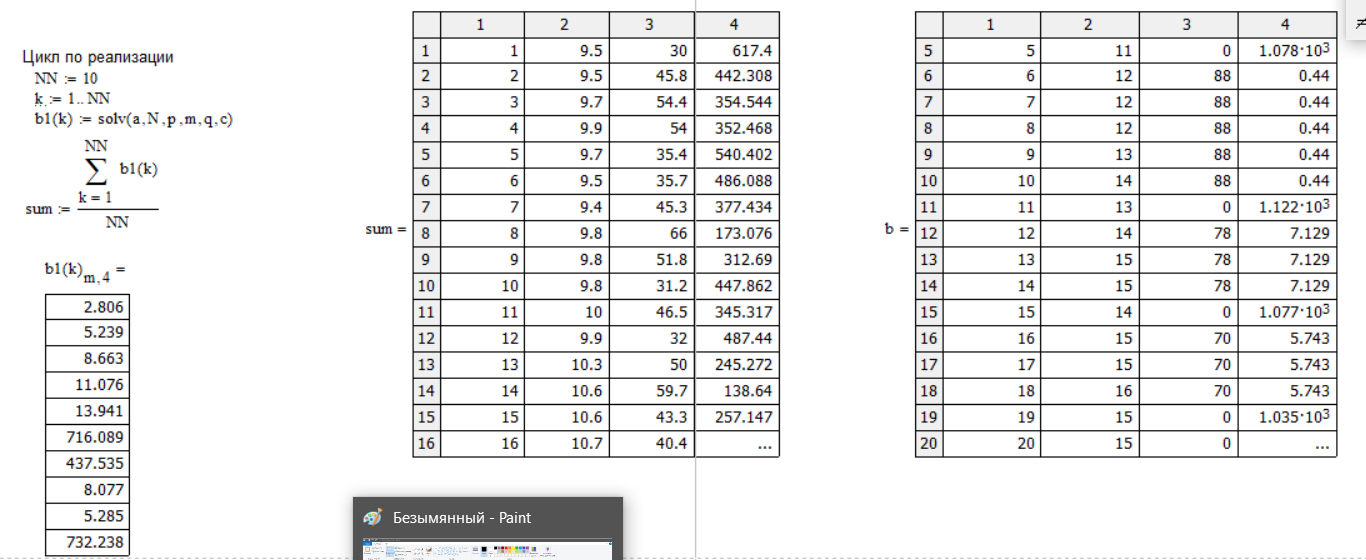
Рисунок 3 – Решение задания 2 пункт б, часть 1

Рисунок 4 – Решение задания 2 пункт б, часть 2
ЗАКЛЮЧЕНИЕ
В ходе лабораторной работы были получены навыки по имитационному моделированию биржевой игры с помощью равномерного датчика случайных чисел. Рассмотренная торговая стратегия показала себя не эффективной, так как первоначально биржевый игрок обладает пакетом из 100 акций стоимостью 10 д.е., совокупной стоимостью в 1000 д.е., при 10 реализациях случайных чисел игрок потерял в среднем 352,444 д.е.