ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Интегрирование способом подстановки
Если заданный интеграл простейшим преобразованием трудно привести (или нельзя привести) к табличному интегралу, то для его отыскания применяют особые приемы. Один из них – интегрирование способом подстановки. Еще этот метод называют способом замены переменной.
Прежде чем перейти к рассмотрению способа подстановки, вспомним понятие дифференциала функции.
О
пределение. Если функция y(x) в точке 
имеет производную 
, то произведение 
является дифференциалом функции у(х) в точке и обозначается dy( 
. Таким образом dy( dx.| dy=  |
Интегрирование способом подстановки заключается в том, что выражение заменяется новой переменной.
Например в интеграле
необходимо произвести замену переменной. Обозначим 
. Найдем дифференциал обеих частей равенства: d( 
Дифференциал данного в интеграле переменного значения необходимо выразить через дифференциал введенной нами переменной.
Имеем:
(таким образом вторую часть подынтегрального выражения выразили через dt).Замену подставляем в интеграл
, и под знаком интеграла получаем выражение, зависящее только от введенной новой переменной t. Если замена проведена правильно, то полученный интеграл должен быть табличным. Таким образом, получаем:
- ответ выражен через вспомогательную переменную t.Чтобы получить окончательный ответ, сделаем обратную замену
:
= 
Подстановка должна выбираться так: если одна часть подынтегрального выражения обозначается за t, то другая должна соответствовать dt с каким-нибудь коэффициентом. В нашем примере
t
dt  |
 |
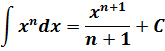Подстановки приводящие к
Пример 1:
.Произведем замену переменной: 2+x=t, dx=dt.
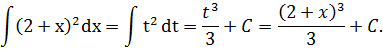
Пример 2.
. Произведем замену: 
.
Пример 3.
. Произведем замену: 
Тогда интеграл примет вид: 
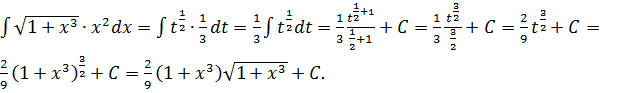
Пример 4.
Произведем замену: 
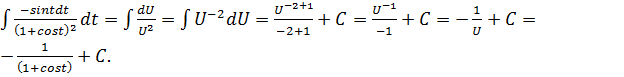
Пример 5.
. Произведем замену: 
= -3 
Пример 6.
Произведем замену: sinx=t; cosxdx=dt
Пример 7.
. Произведем замену: lnx=t; 
+C.Задание №11.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. |  | 1)  |
| 2. |  | 1)  4)-  |
| 3. |  | 1)  |
| 4. |  | 1)  |
| 5. |  | 1)  |
| 6. |  | 1)  |
| 7. |  | 1)  |
| 8. |  | 1)  |