Файл: Методические указания для проведения лабораторной работы Томск 2013 Дисциплина Планирование и организация эксперимента.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Томский политехнический университет
Кафедра компьютерных измерительных систем и метрологии
________________________________________________
Планирование и организация эксперимента
Основы планирования дробного факторного
эксперимента
Методические указания для проведения
лабораторной работы
Томск 2013
Дисциплина: Планирование и организация эксперимента
Время выполнения: 4 часа
Разработали: Казаков В. Ю.
1. Цель работы: изучение основ планирования дробных факторных экспериментов.
2. Используемые технические средства: компьютерный класс, специализированный программный пакет статистических вычислений.
3. Программа работы.
-
Ознакомиться с краткой сводкой общих теоретических положений планирования дробных факторных экспериментов (см. Приложение 1.) -
Выполнить свой вариант задания. -
В зависимости от результата анализа сделать выводы и оформить отчет о проделанной лабораторной работе.
Приложение 1.
Дробный факторный эксперимент
При большом числе факторов ПФЭ требует большого числа опытов. Дробный факторный эксперимент (ДФЭ) позволяет сократить число опытов, но при этом увеличиваются ошибки в определении коэффициентов, а также исключается возможность определения некоторых парных взаимодействий факторов. Ортогональность же матрицы сохраняется.
ДФЭ составляет часть ПФЭ, которая называется дробной репликой. В качестве дробно реплики используются такие части ПФЭ, как 1/2 реплики (полуреплика), 1/4 реплики, 1/8 реплики и т.д. Условное обозначение реплик и количество опытов приведены в таблице.
| Число факторов | Дробная реплика | Обозначение | Количество опытов | |
| ДФЭ | ПФЭ | |||
| 3 4 4 5 5 | ½ реплика от 23 ½ реплика от 24 ¼ реплика от 24 ½ реплика от 25 ¼ реплика от 24 | 2 3 -1 2 4 -1 2 4 -2 2 5-1 2 5 -2 | 4 8 4 16 8 | 8 16 16 32 32 |
Применение ДФЭ эффективно в том случае, если предполагается, что отсутствует или мало влияние на выходной параметр эффектов взаимодействии и соответственно коэффициенты регрессии
при парных произведениях примерно равны нулю. Но в любом случае при большом числе факторов (более 4) ПФЭ становится недостаточно эффективным, так как число опытов с ростом числа факторов увеличивается по показательной функции. Правда, при этом снижаются ошибки в определении коэффициентов полинома, так как все опыты используются для оценки каждого из них. Процесс образования реплик можно проследить на примере. Рассмотрим задачу оценки параметров регрессии
Здесь имеется 8 неизвестных коэффициентов, для которых ПФЭ типа 23 дает 8 уравнений. Если известно, что эффекты взаимодействия малы или незначимы, то число неизвестных сокращается до четырех:
. Для определения данных параметров можно использовать план ПФЭ типа 22 =23–1. Пусть задана матрица ПФЭ типа 22 (см. таблицу 2).| Номер опыта | x0 | x1 | x2 | x1 x2 (x3) | y |
| 1 2 3 4 | + + + + | - + - + | - - + + | + - - + | y1 y2 y3 y4 |
По этой матрице можно получить оценки параметров регрессии
Пусть имеется достаточная уверенность, что в выбранных интервалах варьирования x1 и x2 значение
будет незначимым. Тогда столбец (x1 x2 ) можно использовать для фактора x3. Проведя такой эксперимент, сможем сделать оценку четырех коэффициентов, т.е. получить зависимость
При этом оценки полученных коэффициентов будут смешанными:
смешан с и 
, т.к. столбец 
совпадает со столбцом (
). т.е.
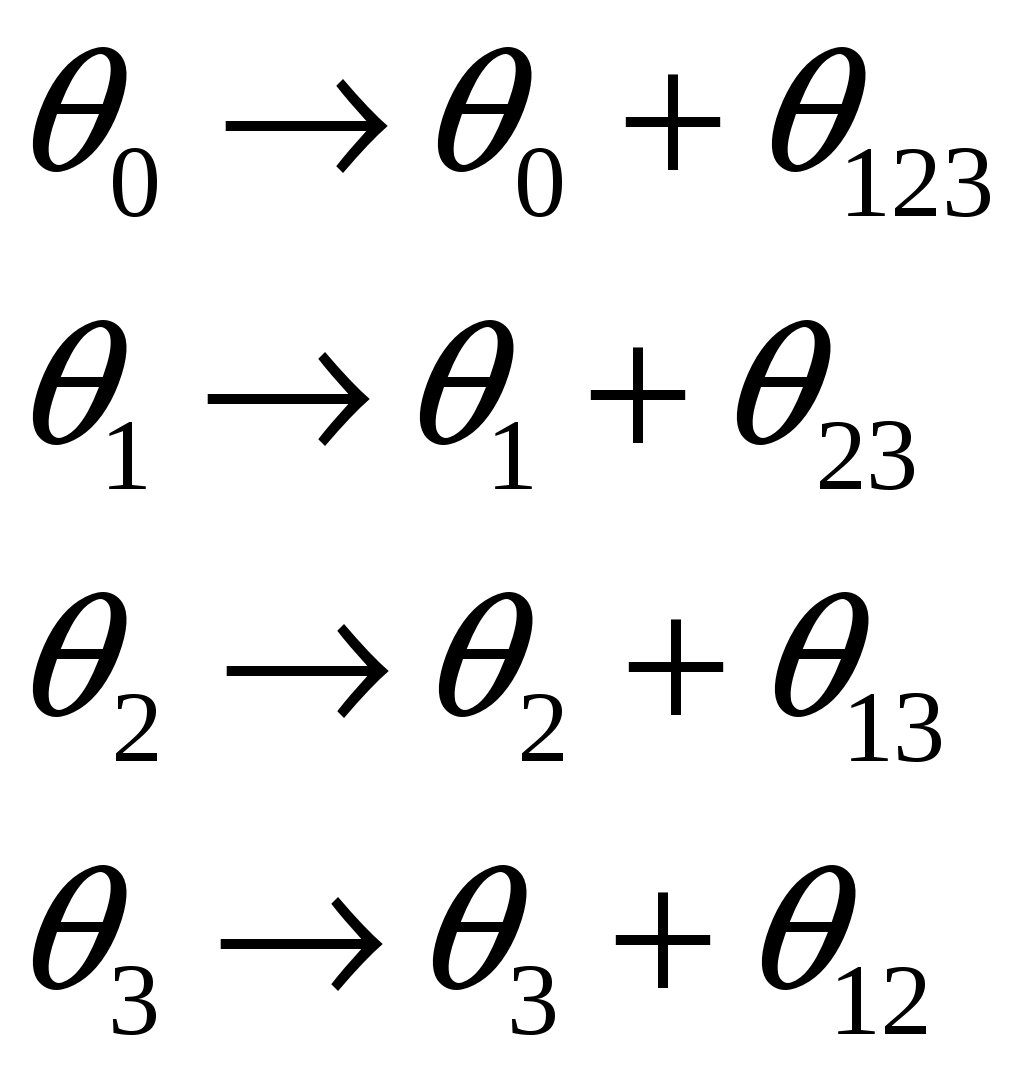
Рассмотренная матрица составляет полуреплику от 23, то есть 2 3 – 1.
Эффективность применения дробных реплик зависит от удачного выбора системы смешивания линейных эффектов с эффектами взаимодействия. При планировании нужно знать, какие эффекты оцениваются совместно, т.e. определить разрешающую способность дробных реплик. Для этого пользуются понятиями "определяющие контрасты (ОК) " и "генерирующие соотношения" (ГС). В рассмотренном случае ДФЭ типа 23–1 могут быть два разных ГС:
Определяющий контраст для нашего случая получается умножением левой и правой частей ГС на x3, т.е.
.Таким образом, произведения столбцов матриц, равные 1 или -1 называются определяющими контрастами, которые помогают найти смешанные эффекты, не изучая матрицу планирования. Для этого нужно последовательно помножить независимые переменные на ОК. Для приведенного примера:
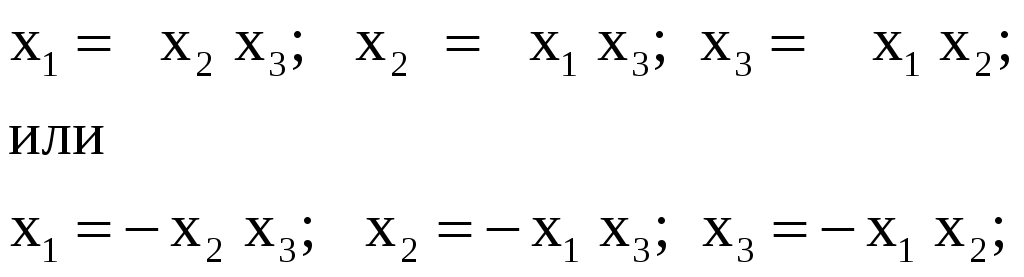
Чтобы получить высокую разрешающую способность реплик, нужно стремиться к такому их плану, чтобы линейные эффекты были смешаны с взаимодействиями более высокого порядка, т.к. они чаще бывают равными нулю.
Пример. Условия эксперимента определены и заданы в таблице
| Фактор xi | Уровни факторов | Интервал варьирования Δxi | ||
| -1 | 0 | 1 | ||
| x1 x2 x3 x4 | 200 3 40 1 | 220 6 100 2 | 240 9 160 3 | 20 3 60 1 |
Для матрицы планирования выбираем полуреплику 24–1 от 24 , заданную генерирующим соотношением
. Определяющий контраст 
. Умножая определяющий контраст последовательно на 
, определяем совместные оценки линейных эффектов и эффектов взаимодействия (смешения)
Матрица планирования и результаты экспериментов приведены в таблице
| Номер опыта | x0 | x1 | x2 | x3 | x4 |  |  |  | y |
| 1 2 3 4 5 6 7 8 | + + + + + + + + | - + - + - + - + | - - + + - - + + | - - - - + + + + | - + + - + - - + | + - - + + - - + | + - + - - + - + | + + - - - - + + | 9 15 25 10 14 5 20 26 |
Вычислив оценки коэффициентов
, получим уравнение регрессии:
Дальнейший анализ проводится также как и в случае ПФЭ.
Задание: варианты задания см.
Короткова Е.И. Практикум по планированию экспериментов. – Томск. Изд-во ТПУ. 2003