Проверяемые задания

Проверяемое задание 1

Тема 1. Основы проектирования в CAD-системах

Задание

Варианты заданий представлены на рис. 1.

Определить:

1) траекторию абсолютного движения заданной точки;

2) амплитуду относительного перемещения;

3) амплитуду угловых перемещений;

4) построить график зависимости относительного перемещения;

5) построить график зависимости линейной скорости при заданной частоте вращения кривошипа; определить максимальное значение линейной скорости.

1	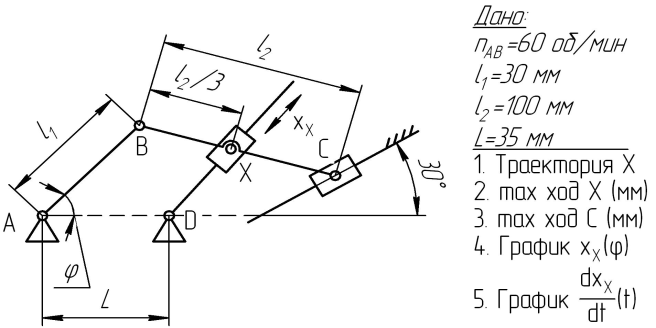2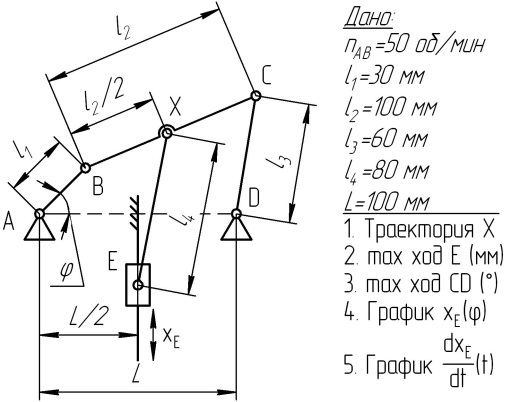
3	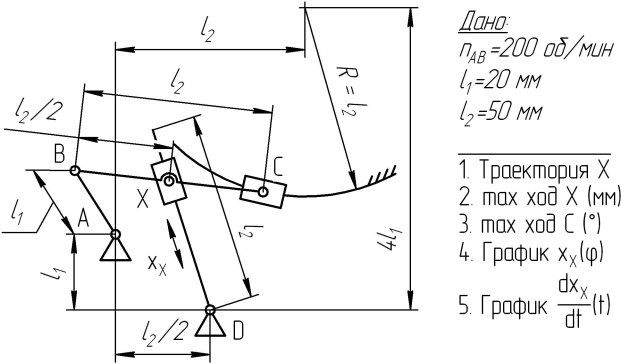4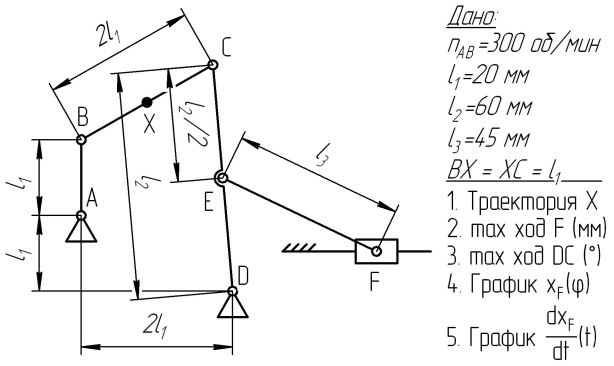
5	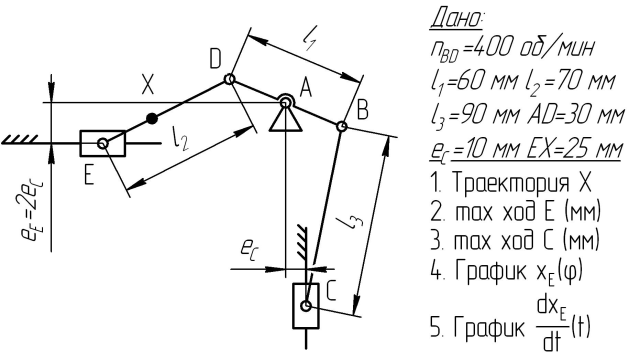6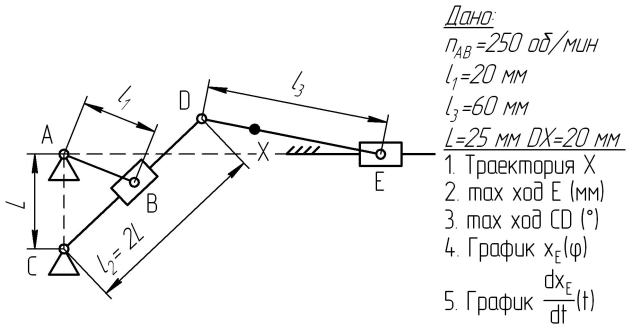
7	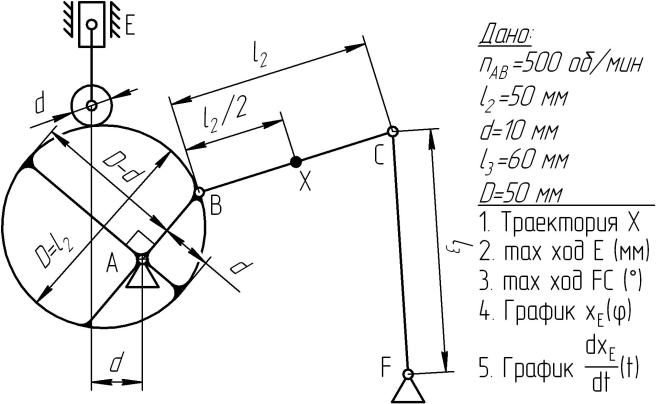8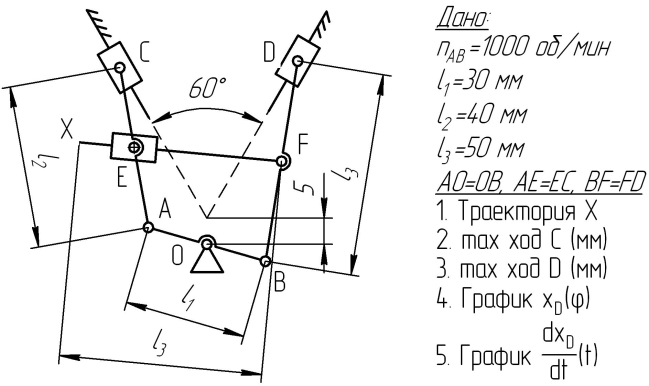
9	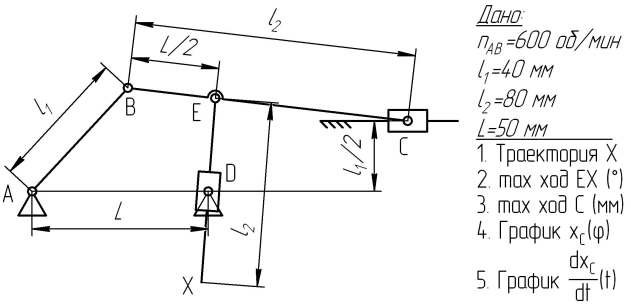10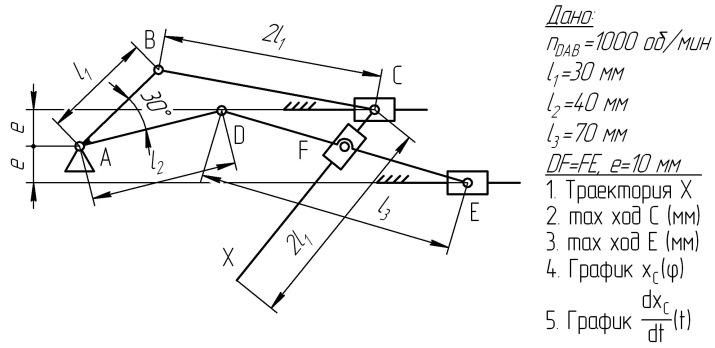

Рис.1. Варианты заданий

Таблица 1

Выбор варианта задания

Первая цифра	Первая буква фамилии	Пример: Жуков Иван – первая буква фамилии соответствует первой цифре 1, вариант 1
1	А, Г, Ж
2	Б, Д, З
3	В, Е, И
4	К, Н, Р
5	У, Ц, Щ
6	Л, О, С
7	Ф, Ч, Э
8	М, П, Т
9	Х, Ш
10	Ю, Я

---

Предъявляется файл «КОМПАС-Фрагмента» (*.frw) с готовой моделью механизма и всеми вспомогательными построениями.

Рекомендации по выполнению задания

Пример. Дана кинематическая схема плоского механизма (рис. 2).

Требуется определить:

1) траекторию абсолютного движения кулисного камня (точки С);

2) амплитуду относительного перемещения кулисного камня относительно кулисы;

3) амплитуду угловых перемещений кулисы;

4) построить график зависимости относительного перемещения кулисного камня относительно кулисы от угла поворота кривошипа;

5) построить график зависимости линейной скорости кулисного камня от времени при условии, что частота вращения кривошипа п = 100 об/мин; определить максимальное значение линейной скорости.

Исходные данные: l₁ = 15 мм, l₂ = 55 мм, l₃ = 80 мм, L = 75 мм. В точках A, B, D звенья имеют шарнирные соединения. Кривошип 1 вращается вокруг точки А с угловой скоростью ω. Кулиса 3 и кулисный камень С образуют поступательную кинематическую пару. Звено 2 жестко соединено с кулисным камнем С под прямым углом, т. е. перпендикулярно кулисе. Стойки 4 и 5 неподвижны.

Требуется определить:

1) траекторию абсолютного движения кулисного камня (точки С);

2) амплитуду относительного перемещения кулисного камня относительно кулисы;

3) амплитуду угловых перемещений кулисы;

4) построить график зависимости относительного перемещения кулисного камня относительно кулисы от угла поворота кривошипа;

5) построить график зависимости линейной скорости кулисного камня от времени при условии, что частота вращения кривошипа п = 100 об/мин; определить максимальное значение линейной скорости.


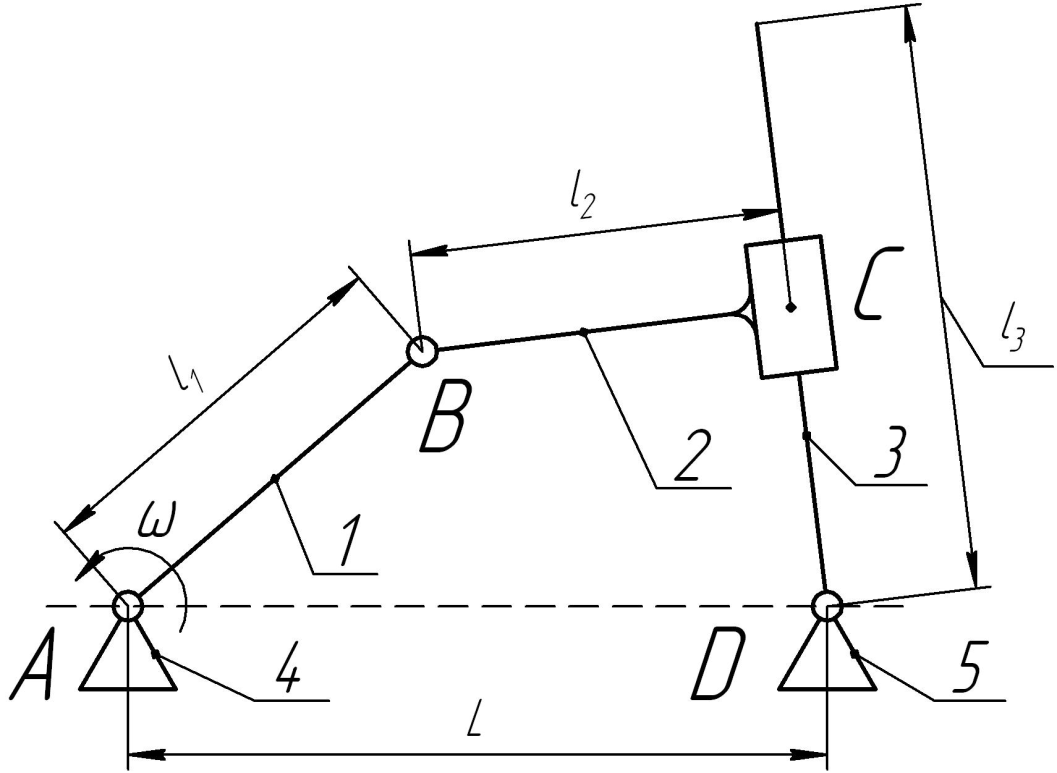
Рис. 2. Схема плоского кривошипно-кулисного механизма

Задание выполняется в программе «Компас». При выполнении работы необходимо оперировать привязками геометрических объектов. В зависимости от выполняемых операций нужно включать и выключать привязки «ближайшая точка», «середина», «точка на кривой» и др.

Поскольку при построении модели используется большое количество объектов (основные геометрические объекты, размеры, вспомогательные построения и др.), то следует пользоваться разнесением их по слоям. Например, в одном слое располагать контуры механизма

---

, во втором − размеры звеньев, в третьем − вспомогательные построения и т. д.

Этап 1. Построение параметрической геометрической модели механизма. При выполнении этапа 1 для задания связей между моделями звеньев механизма необходимо при создании нового фрагмента включить опции ассоциативности и параметризации объектов, а также фиксацию размеров.

1.1. В системном слое (установлен по умолчанию) провести на плоскости изображения 3 линии, как показано на рис. 3. Примечание: привязки, используемые при построении, описаны в таблице 1.1. Для выбора одного из нескольких доступных вариантов привязки при построении отрезка 2 нужно в ходе выполнения команды нажать правую кнопку мыши и из контекстного меню выбрать «Привязка» → <нужный вид привязки>.

Таблица 1.1

Точка	Кинематическая пара	Соединение отрезков	Используемая привязка
В	Шарнир	Начало отрезка 2 в конце отрезка 1	«Ближайшая точка»/«нормаль»
С	Поступательная пара	Конец отрезка 2 внутри отрезка 3	«Точка на кривой»

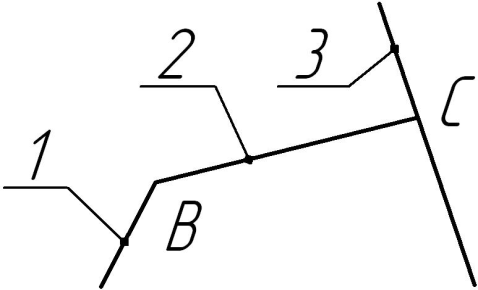
Рис. 3

1.2. Создать новый слой «Размеры», сделать его текущим и проставить размеры звеньев в соответствии с заданием. Размеры должны быть зафиксированными (значения размеров в рамке). Примечание: для отображения ограничений, наложенных на объекты, в версии 8.0 программы «Компас» используется соответствующая кнопка на панели инструментов «Параметризация». Каждому размеру поставить в соответствие имя переменной (рис. 2) − l₁, l₂, l₃, L. После простановки всех размеров слой рекомендуется погасить, сделав текущим системный слой.

1.3. Наложить ограничения на объекты:

− перпендикулярность линий 2 и 3;

− фиксированная точка А (ось кривошипа);

− выравнивание по горизонтали точек А и D(стойки).

Примечание: не следует накладывать ограничение «фиксированная точка» на ось качания кулисы (точка D), поскольку её положение однозначно задаётся размером расстояния AD и ограничением «выравнивание по горизонтали» точек A и D.

1.4. Проверить работоспособность построенной модели. Для этого выделить отрезок 1 (кривошип) и подвигать незафиксированную точку. Вся модель должна двигаться соответствующим образом, повторяя движения кулисного механизма.

---

1.5. Выполнить вспомогательные построения:

− соединить тонкой линией стойки Aи D;

− поставить размер между этой линией и кривошипом (угол поворота кривошипа);

− задать для размера переменную fi;

− на панели переменных¹, на вкладке «Уравнения», создать выражение для этой переменной следующего вида: fi = 90. После ввода уравнения кривошип должен встать в верхнее вертикальное положение;

− пошагово довести значение переменной до fi = 0,001. Примечание: не рекомендуется единовременное изменение значения переменной более чем в 2–5 раз в сторону увеличения или уменьшения, при необходимости такое изменение делается пошагово. Нулевое значение переменной не используется, поскольку при этом значении теряется геометрический смысл размера, обозначенного переменной.

Этап 2. Исследование геометрической модели. При выполнении этапа 2 необходимо отключить опции «Ассоциировать при вводе» и «Параметризовать», которые были включены перед выполнением этапа 1.

2.1. Создать точку на пересечении звеньев 2 и 3 (кулисный камень С).

2.2. Изменить выражение для переменной fi в большую сторону на 10 (0,001; 10; 20 и т. д.).

Повторять п. 2.1 и 2.2 до тех пор, пока кривошип не пройдет один полный оборот. Примечание 1: не рекомендуется делать приращение угла поворота кривошипа больше 10–15°, поскольку это, во-первых, влияет на точность построения, во-вторых, большее изменение значения переменной может завершиться ошибкой программы «Система не имеет решений».

Примечание 2: в данном случае следует использовать значения переменной, входящие в область 0,001 ≤ fi ≤ 350.

2.3. Построить замкнутую кривую Безье, проходящую через все полученные точки, − траекторию движения кулисного камня С (рис. 4).

2.4. Построить две окружности с центром в точке D, касательные к траектории. Разность радиусов построенных окружностей будет равна относительному расстоянию между крайними положениями кулисного камня (амплитуда относительного перемещения камня по кулисе).

2.5. Построить два отрезка из точки D, касательных к траектории, олицетворяющих крайние положения кулисы. Угол между ними будет равен амплитуде угла поворота кулисы (рис. 5).

2.6. Построить зависимость относительного перемещения камня по кулисе от угла поворота кривошипа. Порядок построения кривой проиллюстрирован на рис. 6. Каждому значению

---

fi сопоставляется длина радиус-вектора соответствующей точки траектории относительно точки D. За нулевое положение камня принимается его крайнее положение, максимально приближенное к точке D(в данном случае при нулевом положении кривошипа).

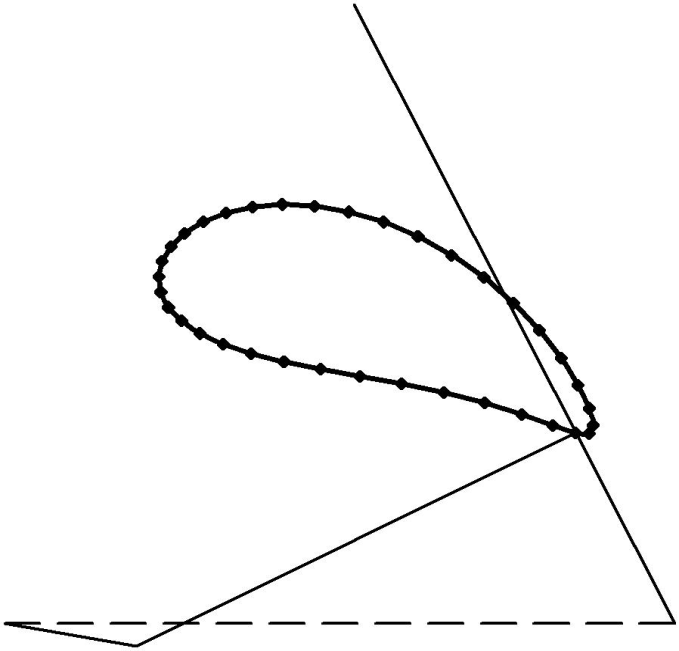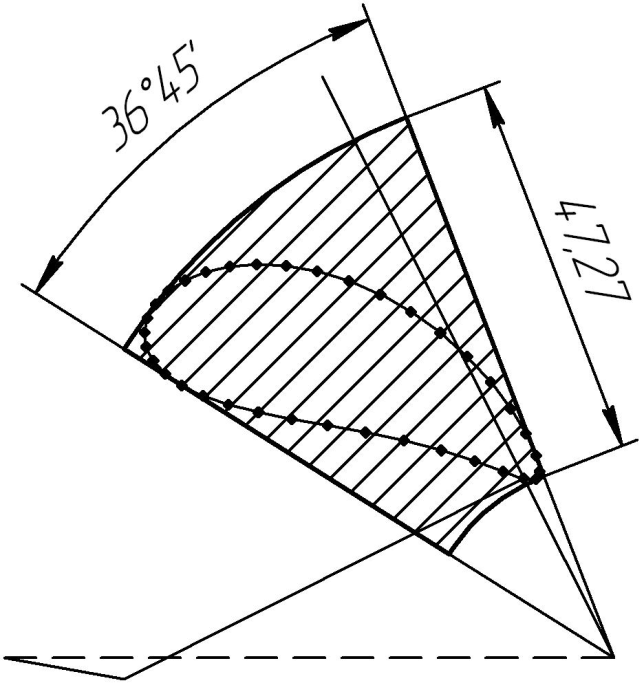Рис. 4.Траектория движения кулисного камня	Рис. 5. Определение максимальных угла и перемещения звеньев механизма

2.7. Построение зависимости скорости от времени. Скорость определяется как первая производная перемещения по времени. Таким образом, задача построения графика изменения скорости от времени сводится к графическому дифференцированию зависимости перемещения от времени (которая при постоянной скорости вращения кривошипа аналогична полученной в п. 2.6). В каждой i-й точке исходного графика x(fi) (начиная со второй) строится вертикальный отрезок длиной |х_i+1 − х_i−1|, который переносится на ось абсцисс. По точкам концов отрезков строится кривая Безье, представляющая собой график зависимости скорости от времени (рис. 7). Шкала оси абсцисс переводится по соотношению

, (1)

где п − частота вращения кривошипа;

fi − шкала угла поворота кривошипа.


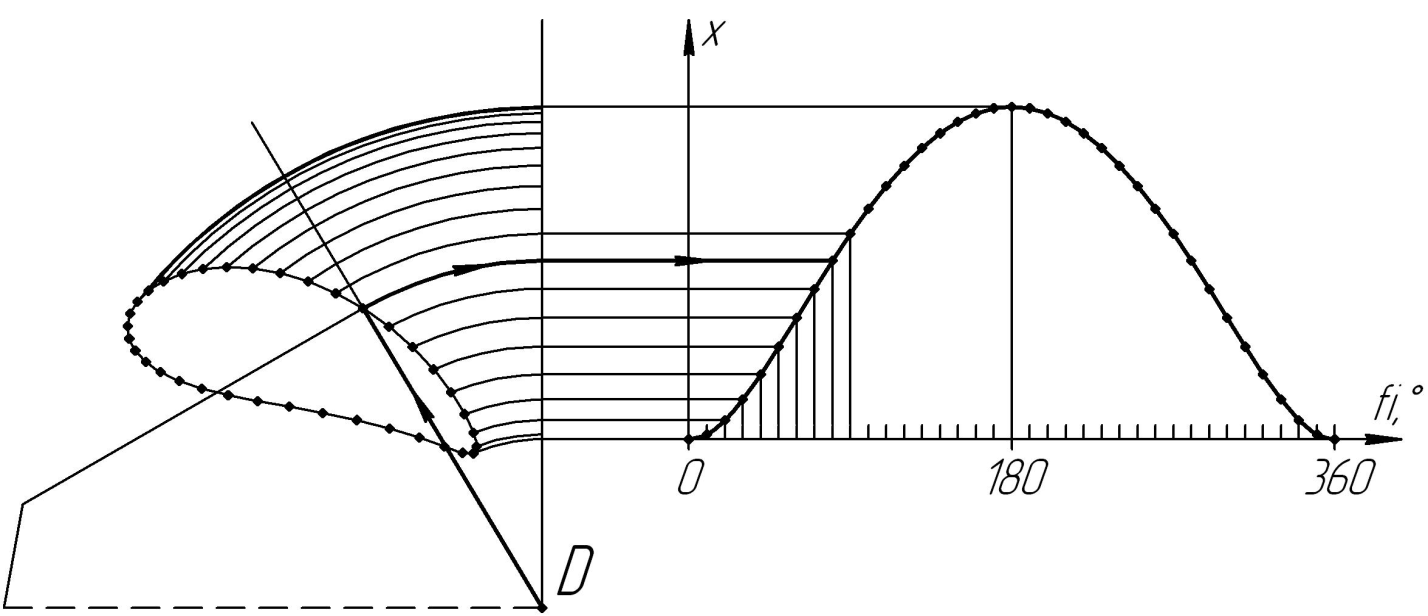
Рис. 6. Зависимость положения камня от угла поворота кривошипа


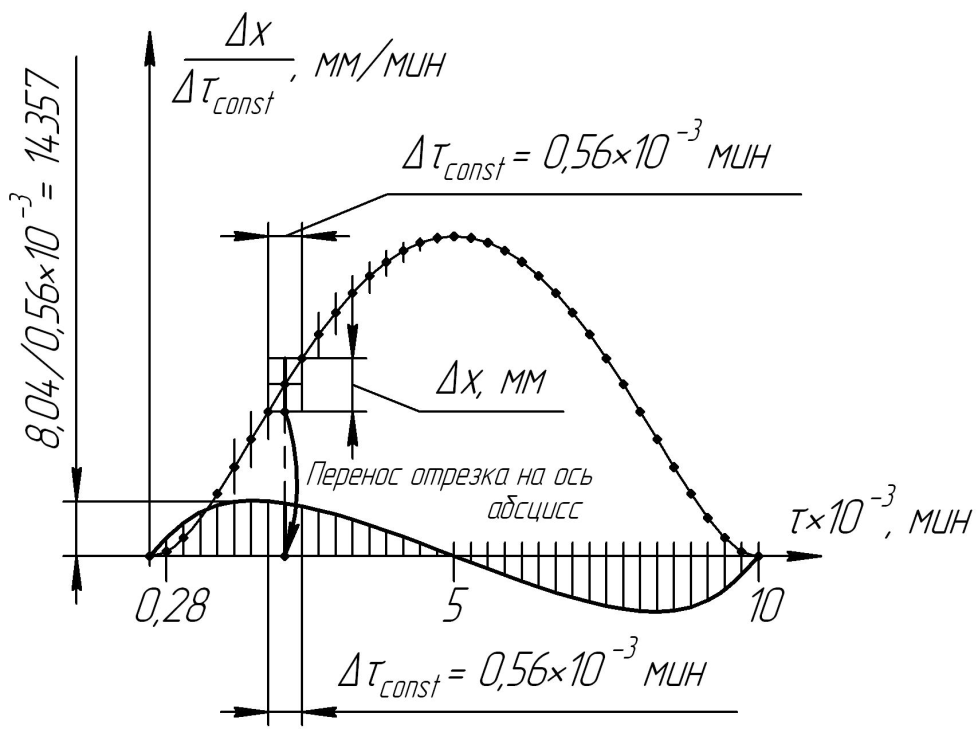
Рис. 7. Построение зависимости скорости от времени

Скорость в мм/мин определяется по формуле

, (2)

где = (х_i+1 − х

---

Смотрите также файлы

• Реализация межпредметных связей в начальной школе на примере урока технологии и математики Муниципальное общеобразовательное учреждение Средняя школа 58 с углублённым изучением предметов естественноматематического цикла.docx

• Анализ производительности труда в организации и пути её повышения.docx

• .doc

• Осветление высокоцветных природных вод северозападного региона сорбционным методом доцент Гладких Светлана Николаевна.pptx

• Хилья Сула Тавасшерна Ручей.docx