BC      3      1
sin A = —— = — = —
              AB      6       2

3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:

              BC       3      1
cos B = —— = — = —
              AB      6       2

 В итоге получается:
sin A = cos B = 1/2.

Или:

sin 30º = cos 60º = 1/2.

Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот.
2
. Значения тригонометрических функций углов в 30°, 45° и 60°.

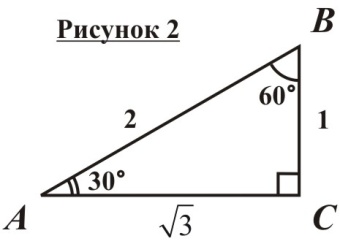
Рассмотрим прямоугольный треугольник с острыми углами в 30° и 60° и меньшим катетом, равным 1 (рисунок 2):

По свойству прямоугольного треугольника с углом в 30°, AB = 2. Катет AC найдем по теореме Пифагора: 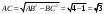. Теперь, зная все стороны треугольника ABC, найдем тригонометрические функции углов в 30° и 60°:

; ;

; .

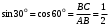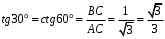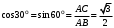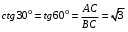Т
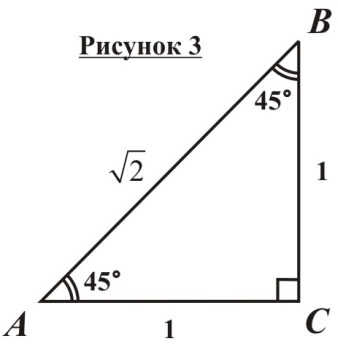
еперь рассмотрим равнобедренный прямоугольный треугольник с катетом, равным 1 (рисунок 3). Оба его острых угла равны по 45°. Найдем гипотенузу по теореме Пифагора: 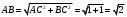. По определению тригонометрических функций острого угла, , .

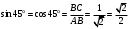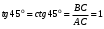Оформим найденные значения тригонометрических функций углов в виде таблицы:

	sin	cos	tg	ctg
30°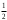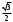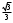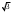
45°		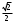	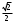1	1
60°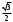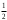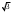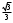

---

Домашнее задание:

---

Смотрите также файлы

• И. Класс Cуммативное оценивание за раздел Основы электростатики i вариант Время выполнения.docx

• Предложения с однородными членами.docx

• Программа наименование учебного предмета Обществознание.docx

• Урока познакомить учащихся с понятием Ситуация криминогенного характера.pptx

• Отчет по лабораторной работе 29 изучение дифракционных решеток. Определение длины световой волны.docx