Федеральное государственное общеобразовательное учреждение высшего образования

<<Чувашский государственный университет имени И.Н. Ульянова>>

Кафедра промышленной электроники

Расчетно-графическая работа

по дисциплине:

<<Теоретические основы цифровой электроники>>

Вариант: №20

Выполнил:

Студент группы: РЭА-?-?

? ? ? Проверил:

Григорьев В.Г.

Чебоксары ?
Содержание

Задание 1…………………………………………………………………………..3

Задание 2………………………………………………………………………......3

Задание 3……………………………………………………………………….….4

Задание 4…………………………………………………………………………..4

Задание 5………………………………………………………………...………...5

Задание 6………………………………………………………………….……….6

Задание 7…………………………………………………………………….…….7

Задание 8…………………………………………………………………….…….9

Задание 9……………………………………………………………...………….11

Задание10…………………………………………………...……..……….…….11

Список использованной литературы…………………………….………….….12

.

Задание 1.

Доказать тождество, исходя из теоремы о необходимом и

достаточном условиях равенства множеств с учетом смысла

операций, приведенных в формулах заданного равенства.
1)

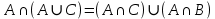
Метод Дистрибутивности: 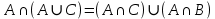, отсюда следует, что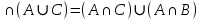



Задание 2.

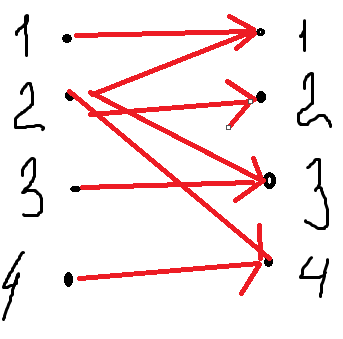
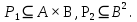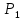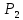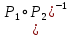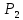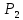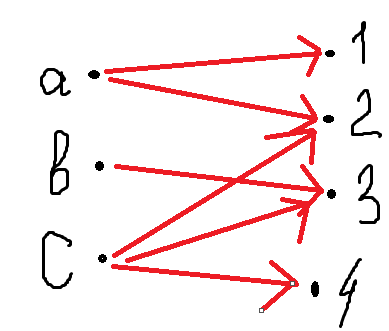
A={a,b,c}, B={1,2,3,4}, Изобразите , графически. Найдите [ ]. Проверьте с помощью матрицы [ ], является ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?

P₁={;;;;;}

P₂={<11>;<2,1>;<2,2>;<2,3>;<2,4>;<3,3>,<4,4>}








[ ]= [ ]=

[ ]=



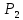
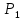
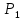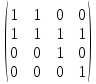
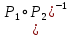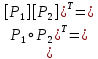
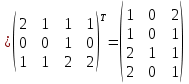
1) [ 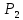]= 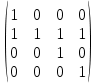– по диагонали нет нулей 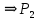– рефлексивно.

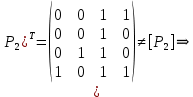
2) 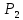– несимметрично.
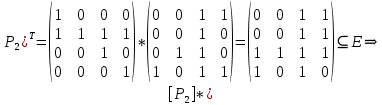
3) 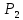– неантисимметрично.

4)



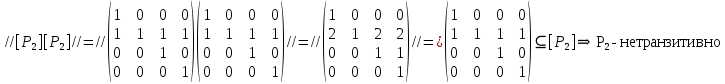
Задание 3.

Определить область определения, область значений би-

нарного отношения Р. Является ли отношение Р рефлексивным,

симметричным, антисимметричным, транзитивным?


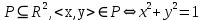
Область определения:



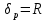
Область значений:



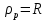
1) Рефлексивность: каждая точка на окружности связана с самой собой, то есть (x, y) R (x, y) для любой точки (x, y) на окружности.

2) Симметричность: если точка (x1, y1) связана с точкой (x2, y2) через отношение R, то и точка (x2, y2) связана с точкой (x1, y1), так как уравнение x^2 + y^2 = 1 симметрично относительно осей координат

3) Транзитивность: если точка (x1, y1) связана с точкой (x2, y2) через отношение R, а точка (x2, y2) связана с точкой (x3, y3), то точка (x1, y1) также связана с точкой (x3, y3), так как все три точки лежат на окружности радиуса 1.
Задание 4.

Является ли алгеброй следующий набор B= ?
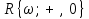Набор B=R{ω;+ , 0} не является алгеброй, так как не выполняется одно из требований определения алгебры. А именно, для того чтобы набор B был алгеброй, он должен быть замкнут относительно операции умножения. Однако, в данном наборе нет обратного элемента для умножения для каждого элемента, кроме нуля. Например, элемент 1/ω не имеет обратного элемента для умножения, так как 1/ω * ω = 1, но 1/ω * x ≠1 для любого другого х из множества B. Таким образом, набор В не удовлетворяет всем требованиям , необходимым для того, чтобы быть алгеброй.


Задание 5.

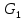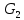Даны графы и . Найдите 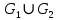, , 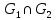, 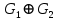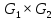. Для графа 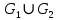найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.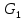






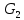
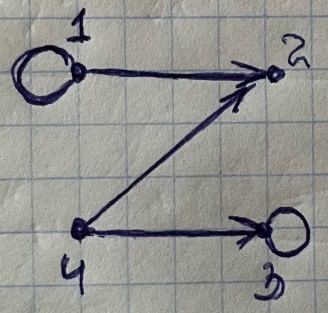
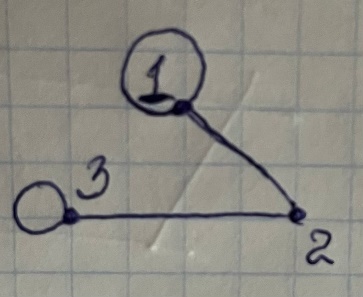
Матрица смежности =

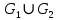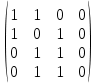
Матрица инцидентности

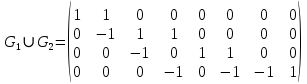
Матрица сильных компонентов для графа


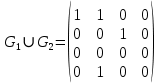
Матрица маршрутов длины 2 для графа

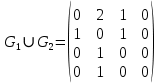
В этой матрице элемент (i,j) показывает количество маршрутов длины 2 из вершины i в вершину j.

Маршруты длины 2, исходящие из вершины 1:

1 -> 2 -> 1

1 -> 2 -> 3

1 -> 4 -> 2

Все эти маршруты начинаются в вершине 1 и имеют длину 2

Задание 6.

Найдите матрицы фундаментальных циклов, фундаментальных разрезов, радиус и диаметр, минимальное множество покрывающих цепей графа G. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным?


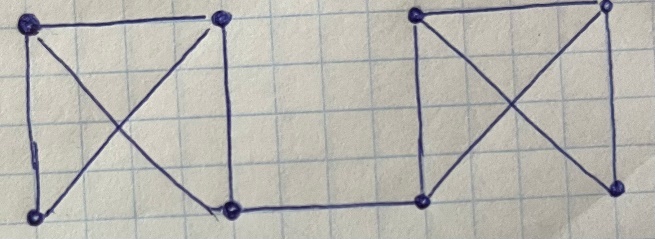
Сначала, построим матрицу смежности для данного графа.


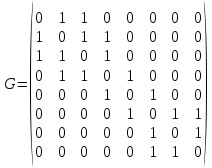
Для того, чтобы ответить на заданные вопросы, давайте рассмотрим их по очереди:

Матрицы фундаментальных циклов и фундаментальных разрезов

Матрицы фундаментальных циклов и фундаментальных разрезов определяются с помощью алгоритма поиска блоков, который основан на алгоритме вычисления определителя матрицы, их конструкция выходит за рамки данного ответа. Можно отметить, что в общем случае количество фундаментальных циклов равно количеству фундаментальных разрезов и равно числу связных компонент графа. В данном случае, граф G является связным, поэтому у него есть один фундаментальный цикл и один фундаментальный разрез.

Радиус и диаметр графа Радиус графа - это наименьшее из наибольших расстояний между всеми парами вершин графа. Диаметр графа - это наибольшее из наименьших расстояний между всеми парами вершин графа. Мы можем вычислить расстояния между всеми парами вершин с помощью алгоритма Флойда-Уоршелла. После выполнения алгоритма, получим следующую матрицу расстояний:


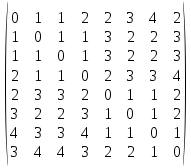
Таким образом, радиус графа G равен 2, так как наименьшее из наибольших расстояний между всеми парами вершин равно 2. Диаметр графа G равен 4, так как наибольшее из наименьших расстояний между всеми парами вершин равно 4.

Минимальное множество покрывающих цепей графа.

Минимальное множество покрывающих цепей графа - это минимальное множество цепей, которые покрывают все рёбра графа. В данном случае, так как граф G является связным, любое остовное дерево содержит минимальное множество покрывающих цепей графа. Одно из остовных деревьев для данного графа выглядит следующим образом:



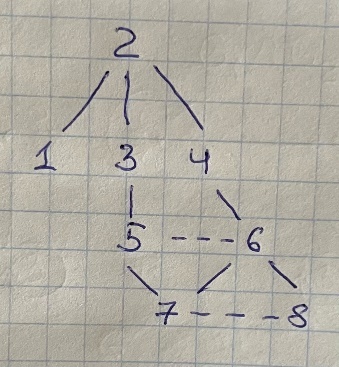
Минимальное множество покрывающих цепей графа состоит из шести цепей: (1,2) (1,3) (2,4) (4,5) (5,6) (6,7)
Эйлеровость графа

Эйлеров граф - это граф, который содержит эйлеров цикл, то есть цикл, который проходит через каждое ребро графа ровно один раз. Граф G не является эйлеровым, так как в нем есть вершины нечётной степени (вершины 1, 3, 5 и 7).

Планарность графа

Планарный граф - это граф, который может быть нарисован на плоскости без пересечения рёбер. Чтобы определить, является ли граф планарным, можно использовать формулу Эйлера для плоских графов: V - E + F = 2, где V - количество вершин, E - количество рёбер, F - количество граней.
Для графа G:

V = 8

E = 21

F = ?
Чтобы найти количество граней, можно воспользоваться формулой Эйлера для связных плоских графов без петель:

F = E - V + 1.

Таким образом: F = 21 - 8 + 1 = 14 Получается, что граф G имеет 14 граней.
Однако это не означает, что граф G планарный. Можно использовать теорему Понтрягина-Куратовского, чтобы проверить, является ли граф G планарным. Согласно этой теореме, граф планарный тогда и только тогда, когда он не содержит подграфа, гомеоморфного K5 или K3,3.

K5 - полный граф на 5 вершинах, а K3,3 - двудольный граф с 3 вершинами в каждой доле, в котором каждая вершина первой доли соединена с каждой вершиной второй доли.

Можно проверить, содержит ли граф G подграф, гомеоморфный K5 или K3,3. Однако можно заметить, что граф G имеет цикл длиной 4, который содержит рёбра (2,4), (4,5), (5,6) и (6,7). Это означает, что граф G содержит подграф, гомеоморфный K3,3, и, следовательно, не является планарным

Задание 7.

Проверить тождественность заданного равенства.


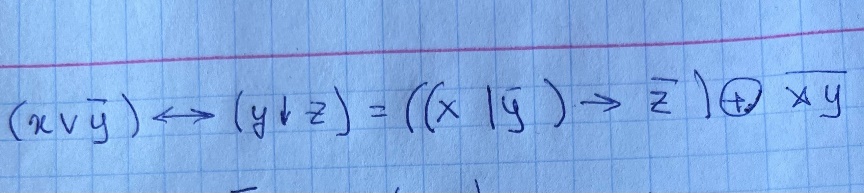
Правая сторона:



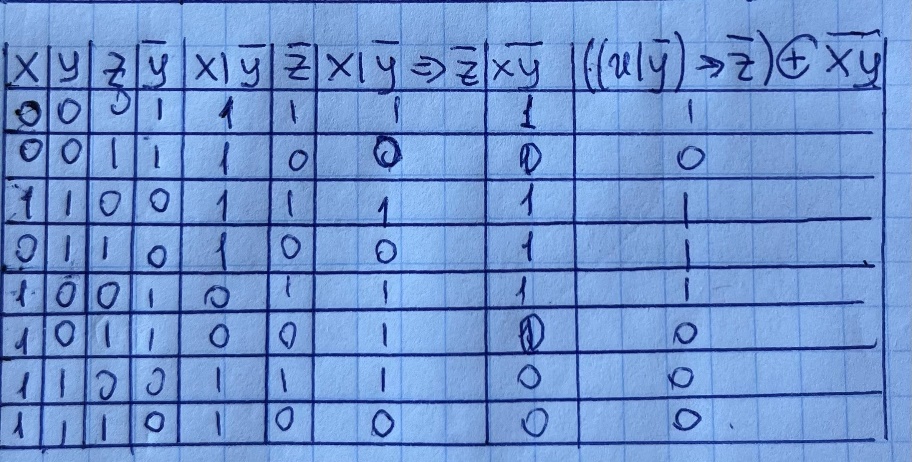
Левая сторона:


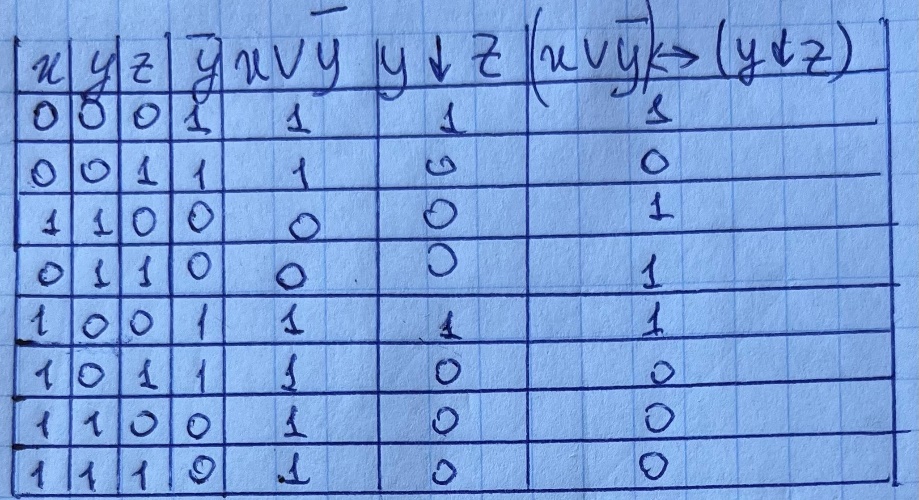
Задание 8.

Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции 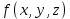двумя способами:

а) методом Квайна б) с помощью карт Карно

Каким классам Поста принадлежит эта функция?


а)

x	y	z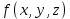
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

	*	*
	*		*
			*	*
				*	*

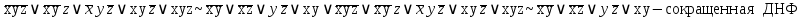
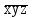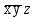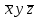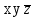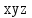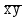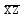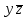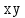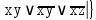тупиковые и минимальные ДНФ.
б)







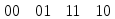
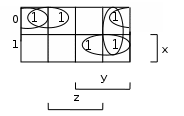
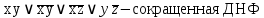
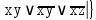тупиковые и минимальные ДНФ.
1) 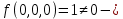функция не сохраняет ноль

2) 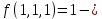функция сохраняет единицу

3) 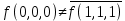– функция несамодвойственная.

4) 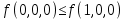– функция немонотонная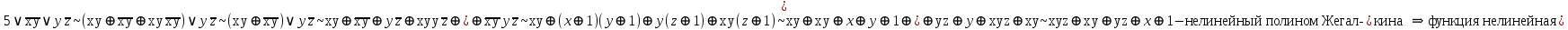



Задание 9.

Является ли полной система функций J= ?
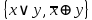Для того чтобы определить, является ли заданная система функций J полной, необходимо проверить, может ли с её помощью выразиться любая булева функция.

В данной системе функций J содержится 2 функции:

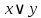(логическое ИЛИ)

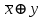(исключающее ИЛИ)

С помощью данных функций можно выразить след. базовые булевы функции :

1. 
   НУЛЬ (0) можно выразить, используя логическое ИЛИ и отрицание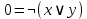
   
2. 
   Конъюнкция (логическое И) - можно выразить, используя исключающее ИЛИ и отрицание: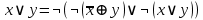
   
3. 
   Отрицание (логическое НЕ) - можно выразить, используя исключающее ИЛИ: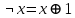
   

Таким образом, система функций J является полной, так как с ее помощью можно выразить любую булеву функцию.
Задание 10.

Сколько существует десятичных чисел, структура кото- рых удовлетворяет заданным условиям?

Количество разрядов числа равно 6. Первые две цифры числа в сумме равны, а последние две цифры четные.
Первые две цифры числа в сумме равны, значит, мы можем рассмотреть все возможные пары цифр, которые в сумме дают одно и то же число. Есть 45 таких пар: 00, 11, 22, 33, 44, 55, 66, 77, 88, 99, 10, 21, 32, 43, 54, 65, 76, 87, 98, 20, 31, 42, 53, 64, 75, 86, 97, 30, 41, 52, 63, 74, 85, 96, 40, 51, 62, 73, 84, 95, 50, 61, 72, 83, 94, 60, 71, 82, 93, 70, 81, 92, 80, 91, 90.

Последние две цифры числа четные, то есть могут быть любой из следующих комбинаций: 00, 02, 04, 06, 08, 20, 22, 24, 26, 28, 40, 42, 44, 46, 48, 60, 62, 64, 66, 68, 80, 82, 84, 86, 88, 10, 12, 14, 16, 18, 30, 32, 34, 36, 38, 50, 52, 54, 56, 58, 70, 72, 74, 76, 78, 90, 92, 94, 96, 98.
Таким образом, количество десятичных чисел, удовлетворяющих обоим условиям, равно произведению количества возможных комбинаций первых двух цифр и последних двух цифр: 45 * 25 = 1125. Таким образом, существует 1125 десятичных чисел, структура которых удовлетворяет заданным условиям.

Список использованной литературы

Учебник С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной математики11>

---

Смотрите также файлы

• Тсінік хат Цифрлы сауаттылы оу пні.docx

• Философия права Гегеля.pdf

• Консультирование тревожных клиентов.docx

• Проблемнопоисковая деятельность младших школьников при изучении вычислительных приемов автореферат.pdf

• Царство Грибы Общая характеристика.docx