Министерство Российской Федерации

по связи и информатизации

Московский технический университет связи и информатики

_________________________________________________________________

Кафедра физики
Лабораторная работа №1

Знакомство с измерительными приборами.

Методика обработки результатов измерений.

Определение плотности твердого тела.
Выполнила: А.Г. Ворона

Проверила: Л.В. Осичева


Москва 2023

Цель работы - знакомство с измерительными приборами и методом обработки физических измерений.

Основные законы:

Плотность тела определяется по формуле p=m/V.

Где m – масса тела, V – объем тела.

Объем тела находиться с помощью измерения фигуры с помощью штангенциркуля.

Масса тела указана в таблице.















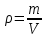
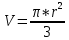
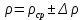
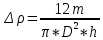
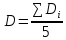
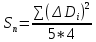
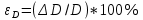
штангенциркуль ШЦ-II с погрешностью 0,1 мм

Вариант 4.

Таблица 1

5	54,1	0	0
Номер наблюдения i	Di мм	ΔDi = D-Di мм	ΔDi2 мм2
1	54,4	0	0
2	54,4	0	0
3	54,3	0,1	0,01
4	54,1	0,2	0,04
5	54,1	0	0

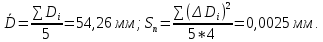
Среднеквадратичная ошибка измерений диаметра цилиндра:

---

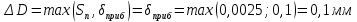
Округление ошибки:


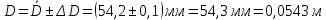
Относительная ошибка данного результата составляет:


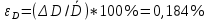
Обработка результатов косвенного измерения плотности конуса

Плотность конуса вычисляется по формуле:



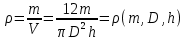
где h – высота конуса, D – диаметр конуса, m – масса конуса

D, h, m находятся в результате прямых измерений.

m = 90,90 ± 0,01 г

В качестве результатов прямых измерений величины h возьмем следующие:

Таблица 2

Номер наблюдения i	Hi мм	ΔHi = H-Hi мм	ΔHi2 мм2
1	76,5	0	0
2	76,7	-0,2	0,04
3	76,5	0	0
4	76,4	0,1	0,01
5	76,4	0,1	0,01

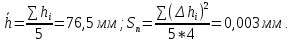
Среднеквадратичная ошибка измерений диаметра цилиндра:



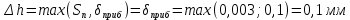
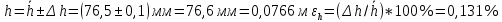
Среднее значение массы:


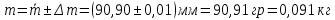
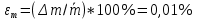
π = 3,14 при этом

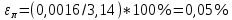
Вычислим среднюю плотность:


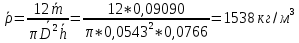
Найдём абсолютную ошибку косвенного измерения плотности по формуле:

---

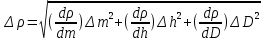
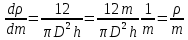
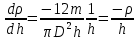
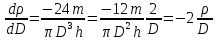
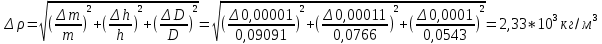
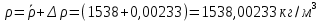
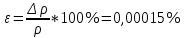
Вопросы 4.1-4.3

4.1 Абсолютная и относительная ошибки. Какая из них характеризует качество измерения различных величин?

Ответ: Абсолютная и относительная ошибки — это характеристики точности измерений и оценки отклонения полученных результатов от истинных значений.

Абсолютная ошибка — это разница между измеренным значением и истинным значением измеряемой величины. Она показывает, насколько измеренное значение отклоняется от истинного значения, и измеряется в тех же единицах, что и сама величина.

Относительная ошибка — это абсолютная ошибка, отнесенная к истинному значению измеряемой величины. Она показывает, какую долю отклонения составляет абсолютная ошибка от истинного значения и измеряется в процентах.

Обе ошибки являются важными характеристиками точности измерений, и выбор той или иной зависит от задачи. Если нужно оценить точность измерения в абсолютном выражении, то следует использовать абсолютную ошибку. Если же нужно оценить точность измерения в относительном выражении, то следует использовать относительную ошибку.

В целом, относительная ошибка более удобна, так как она не зависит от единиц измерения и позволяет сравнивать точность измерений разных величин.
4.2 Правильно ли записаны результаты: т = (479,85±2,35) г, h = (6.71± 0.37) м²

Ответ: нет, результаты не записаны правильно.

• 
  Для массы t правильно записать так: t = 479,85 ± 2,35 г.
  
• 
  Для площади h правильно записать так: h = (6,71 ± 0,37) м².
  

• 
  4.3 Найти ускорение свободного падения, если длина маятника І = (139,5
  

0,5) см, период колебаний Т = (2,38±0,02) с. Рассчитайте абсолютную и относительные ошибки косвенных измерений.

Ответ: для расчета ускорения свободного падения воспользуемся формулой математического маятника:

g = (4 * π² * L) / T²

где g - ускорение свободного падения, L - длина маятника, T - период колебаний.

Подставляя значения, получаем:

g = (4 * π² * 139,5 см) / (2,38 с)²

g ≈ 981,8 см/с²

Для расчета абсолютной ошибки воспользуемся формулой:

Δg = |dg/dL| * ΔL + |dg/dT| * ΔT

где ΔL и ΔT - абсолютные погрешности измерений L и T, соответственно.

Вычислим производные:

---

dg/dL = 4 * π² / T² ≈ 6,62 с^-2

dg/dT = -8 * π² * L / T³ ≈ -1,15 * 10³ с^-2

Подставляя значения, получаем:

Δg = |6,62 с^-2| * 0,5 см + |-1,15 * 10³ с^-2| * 0,02 с

Δg ≈ 11,64 см/с²

Для расчета относительной ошибки воспользуемся формулой:

δg = Δg / g

Подставляя значения, получаем:

δg = 11,64 см/с² / 981,8 см/с² ≈ 0,012

Ответ: ускорение свободного падения g ≈ 981,8 см/с², абсолютная ошибка Δg ≈ 11,64 см/с², относительная ошибка δg ≈ 0,012.

---

Смотрите также файлы

• Билалова К. Р.docx

• Доклад Карл Фейерабенд.docx

• Министерство науки и высшего образования российской федерации федеральное государственное автономное образовательное учреждение высшего образования.docx

• Студентки 2 курса 2 группы очной формы обучения Мамедовой Альбины Владимировны.docx

• Решение задач Заключение Список использованных источников Введение Уравнения. Можно утверждать наверняка, что не найдется ни одного человека, который бы не был знаком с ними. Дети сызмала начинают решать задачи с иксом.rtf