Добавлен: 10.01.2024
Просмотров: 88
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
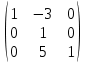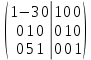
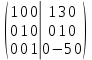
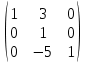
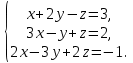
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТАЗадача 1. Найти матрицу, обратную матрице .Решение: Для вычисления обратной матрицы запишем матрицу , дописав к ней справа единичную матрицу:К 1 строке добавляем 2 строку, умноженную на 3; от 3 строки отнимаем 2 строку, умноженную на 5:Ответ: Задача 2. Решить СЛАУ Ответ: {x + 2y –z = 3 (1){3x – y + z = 2 (2){2x - 3y + z = -1 (3)прибавим (1) и (2),получим 4х + у = 5прибавим (1) и (3),получим 3х - у = 27х = 7х = 14*1 + у = 5у = 5 - 4у = 1подставим в (1)1 + 2 - z = 3z = 0Ответ (1 ; 1; 0)Задача 3. Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен: а) ровно 6-ти изделиям;б) более чем 7-ми изделиям;в) хотя бы одному изделию;г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.Решение.Вероятность того, что изделию не будет присвоен знак «изделие высшего качества» равна q=1-p=1-0.2=0.8а) P9(6)= 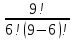· p6· q9-6 = 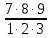· 0,000064 · 0,512 = 0,0028б) P9(m>7) = P9(8 или 9) = P9(8)+P9(9)= 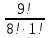·p8·q1 + 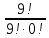·p9·q0= =9·0,28·0,8+1·0,29·1=0,000019 в) событие G – изделию присвоен знак «изделие высшего качества»;событие Ḡ – ни одному изделию не будет присвоен знак «изделие высшего качества»
P(G)=1-P(Ḡ)=1-P9=1- ·p0 · q9 =1-0,13=0,87г) 9· 0,2 - 0,8 ≤ k0 ≤ 9 · 0,2 + 0,29 · 0,2 – 0,8 ≤ k0 ≤ 9 · 0,2 + 0,21 ≤ k0 ≤ 21 ≤ k0 ≤ 2Наивероятнейшее количество изделий у нас получилось 1 или 2, значит их вероятности равны. Найдем P9(1)=P9(2)P9(1)=P9(2)=
· p2 · q7 = 
· 0,04 · 0,21 = 0,302
P(G)=1-P(Ḡ)=1-P9=1- 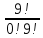·p0 · q9 =1-0,13=0,87г) 9· 0,2 - 0,8 ≤ k0 ≤ 9 · 0,2 + 0,29 · 0,2 – 0,8 ≤ k0 ≤ 9 · 0,2 + 0,21 ≤ k0 ≤ 21 ≤ k0 ≤ 2Наивероятнейшее количество изделий у нас получилось 1 или 2, значит их вероятности равны. Найдем P9(1)=P9(2)P9(1)=P9(2)=
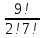· p2 · q7 = 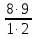· 0,04 · 0,21 = 0,302