Файл: Пермский национальный исследовательский политехнический университет.docx
Добавлен: 10.01.2024
Просмотров: 40
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего образования
Пермский национальный исследовательский политехнический университет
| Факультет: | Аэрокосмический |
| Специальность: | 24.05.02 Проектирование авиационных |
| | и ракетных двигателей |
| Специализация: | Проектирование авиационных двигателей |
| | и энергетических установок |
| Кафедра: | Авиационные двигатели |
Дисциплина «Механика жидкости и газа»
Отчёт о решении задачи №2
| На тему | Определение силы воздействия |
| потока на плоскую пластину | |
| Студенты | Баканина Маргарита Яковлевна | ( | | ) |
| | | | | |
| Группа | АД-19-2с | | | |
| Принял: | | | |
| | ( | Матюнин В.П. | ) |
| Дата: | |
Пермь 2022
ЗАДАНИЕ
Определить силу воздействия потока на плоскую пластину.
ВВЕДЕНИЕ
Представленная задача помогает сформировать понимание о том, как ведет себя поток воздуха при огибании тел.
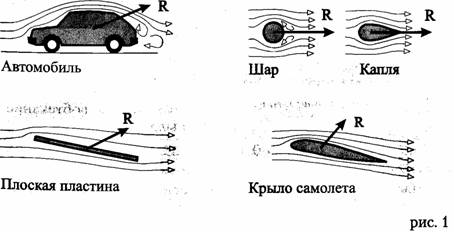
Рис.1.Возникновение подъемной силы при огибании тел потоком воздуха
В данном случае будет рассмотрено самое простое тело – пластина. Известно, что характер воздействия потока на тело зависит от угла атаки - угла между направлением вектора скорости набегающего на тело потока и характерным продольным направлением, выбранным на теле. Для решения этой задачи необходимо сформировать понятие об аэродинамической силе, подъемной силе, силе сопротивления, определить физическую модель и подходящую для нее математическую модель. А также следует определить, имеет ли достоверное решение данная задача и нет ли каких-либо ограничений для полученного решения.
1.ФИЗИЧЕСКАЯ МОДЕЛЬ
Как уже было сказано, в качестве тела будет выбрана тонкая пластина длиной 1 м и шириной 1м. Рассматривать процессы следует в плоскости параллельной направлению течения потока.
Итак, в результате взаимодействия твердого тела с набегающим потоком воздуха, образуется полная аэродинамическая сила R. Эта полная аэродинамическая сила складывается из подъемной силы Y (вертикальная составляющая аэродинамической силы, направлена перпендикулярно набегающему потоку в сторону пониженного давления) и силы сопротивления (горизонтальная составляющая аэродинамической силы, направлена параллельно набегающему потоку).
Величина подъемной силы сильно зависит от угла, под которым набегающий поток «ударяется» в пластину. При увеличении угла атаки, точка деления потока воздуха смещается на нижнюю поверхность профиля. Путь частиц по верхней поверхности увеличивается. Из-за этого возрастает разница давлений и увеличивается подъемная сила.
Теперь следует рассмотреть процесс обтекания пластины воздушным потоком более подробно.
Пусть угол атаки
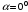 . Тогда пластина установлена вдоль потока. В этом случае поток воздуха пластиной не отклоняется и подъемная сила Y = 0. Сопротивление X минимально, но не равно нулю. Оно будет обеспечиваться сопротивлением трения молекул воздуха о поверхность пластины. Полная аэродинамическая сила R минимальна и совпадает с силой сопротивления
. Тогда пластина установлена вдоль потока. В этом случае поток воздуха пластиной не отклоняется и подъемная сила Y = 0. Сопротивление X минимально, но не равно нулю. Оно будет обеспечиваться сопротивлением трения молекул воздуха о поверхность пластины. Полная аэродинамическая сила R минимальна и совпадает с силой сопротивления
X.
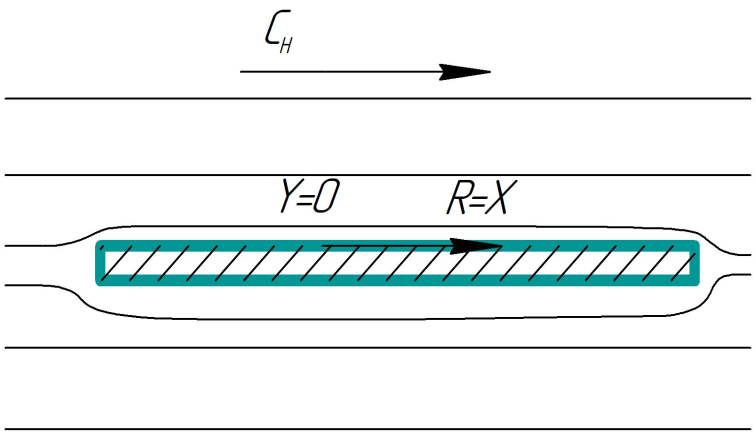
Рис. 2. Положение пластины при угле атаки α=0
Пусть угол атаки
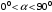 , но меньше критического значения. При данном угле атаки возникает сужение струек сверху пластины и расширение снизу, свидетельствующее об увеличении скорости воздуха над пластиной и уменьшении скорости под пластиной. Из уравнения Бернулли – уравнения связи между скоростью и давлением известно: где скорость больше – давление меньше, и наоборот. Следовательно, давление сверху пластины – меньше, чем давление снизу. В результате разности давлений возникнет полная аэродинамическая сила. Она направлена в сторону меньшего давления ( назад и вверх) (рис.3).
, но меньше критического значения. При данном угле атаки возникает сужение струек сверху пластины и расширение снизу, свидетельствующее об увеличении скорости воздуха над пластиной и уменьшении скорости под пластиной. Из уравнения Бернулли – уравнения связи между скоростью и давлением известно: где скорость больше – давление меньше, и наоборот. Следовательно, давление сверху пластины – меньше, чем давление снизу. В результате разности давлений возникнет полная аэродинамическая сила. Она направлена в сторону меньшего давления ( назад и вверх) (рис.3).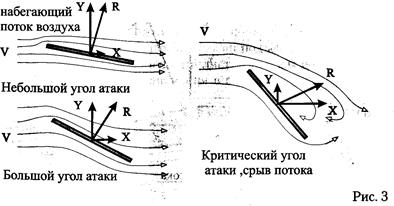
Рис.3.Положение пластины при угле атаки 0<α<90
Угол атаки
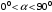 , но близок к критическому значению. Тогда наблюдается следующая картина: по мере постепенного увеличения угла атаки и увеличения скоса потока подъемная сила увеличивается. Очевидно, что сопротивление тоже растет, но на малых углах атаки подъемная сила растет значительно быстрее, чем сопротивление.
, но близок к критическому значению. Тогда наблюдается следующая картина: по мере постепенного увеличения угла атаки и увеличения скоса потока подъемная сила увеличивается. Очевидно, что сопротивление тоже растет, но на малых углах атаки подъемная сила растет значительно быстрее, чем сопротивление.При дальнейшем увеличении угла атаки воздушному потоку становится все труднее обтекать пластину. Подъемная сила продолжает увеличиваться, но медленнее, чем раньше, а сопротивление растет все быстрее и быстрее, постепенно обгоняя рост подъемной силы. В результате полная аэродинамическая сила R начинает отклоняться вправо (рис.4).

Рис.4. Положение пластинки при угле атаки α, близком к критическому
После определенного угла атаки воздушные струйки оказываются не в состоянии плавно обтекать верхнюю поверхность пластины. За пластиной образуется мощный вихрь. Подъемная сила резко падает, а сопротивление увеличивается. Такое явление называется срывом потока (рис.5). Образование вихрей требует построения сложной математической модели, поэтому, для упрощения, в условиях данной задачи они не рассматриваются.

Рис.5.Положение пластинки при критическом угле атаки α
Пусть угол атаки
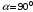 . Обтекание будет также симметричным, как и при горизонтальном обтекании и скорости потока сверху и снизу будут одинакового значения. Происходит резкое торможение потока перед пластинкой, поджатие струек у ее краев и образование непосредственно за краем пластинки разрежения и больших вихрей. Эти вихри заполняют всю область за пластинкой. Перед пластинкой давление будет больше, чем в невозмущенном потоке. А за пластинкой , вследствие разрежения, давление уменьшится. При таком обтекании на пластинку действует сила лобового сопротивления (R=X). Аналогично, из-за образования вихрей, данная физическая модель не рассматривается.
. Обтекание будет также симметричным, как и при горизонтальном обтекании и скорости потока сверху и снизу будут одинакового значения. Происходит резкое торможение потока перед пластинкой, поджатие струек у ее краев и образование непосредственно за краем пластинки разрежения и больших вихрей. Эти вихри заполняют всю область за пластинкой. Перед пластинкой давление будет больше, чем в невозмущенном потоке. А за пластинкой , вследствие разрежения, давление уменьшится. При таком обтекании на пластинку действует сила лобового сопротивления (R=X). Аналогично, из-за образования вихрей, данная физическая модель не рассматривается.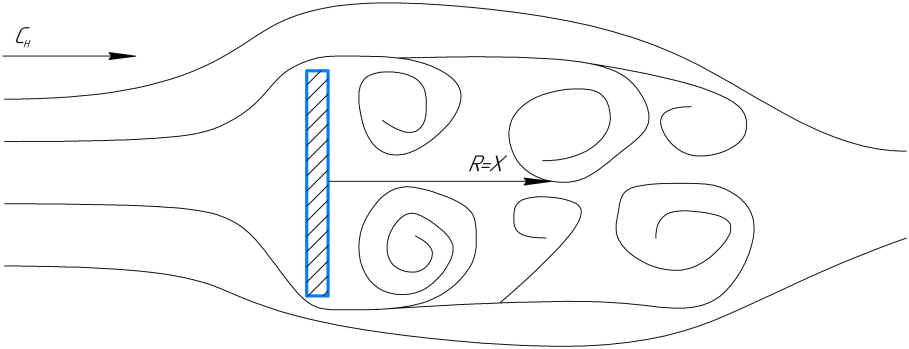
Рис.6.Положение пластинки при угле атаки α=90º
Итак, поскольку использовать в данной задаче проще физическую модель положения пластики при угле атаки от 0º до некого критического угла, следует описать, как распределяется скорость потока в данном случае.
На рис. 7 изображено разложение скорости потока с на нормальную сn и тангенциальную сτ составляющие. Тангенциальная составляющая сτ тормозится на поверхности пластины, переходя в работу трения (гидросопротивления), необратимо рассеивающуюся в виде тепла в пространстве. Пластина принята непроницаемой, значит нормальная составляющая сn обнуляется, тем самым создавая область повышенного давления.
Скорость движения слоёв сn уменьшается по мере уменьшения расстояния до стенки вплоть до cn=0 при n=0, а давление, согласно уравнению Бернулли, увеличивается.
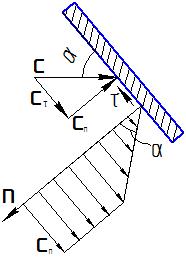
Рис.7. Распределение скорости потока при угле атаки меньше критического
При решении задачи не следует учитывать, как торможение тангенциальной составляющей влияет на давление вдоль пластины, т.к. сила давления значительно больше силы трения. Тогда давление на нижней части пластины возрастает за счёт торможения только нормальной составляющей, и оно называется давлением частичного торможения:
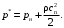 (1)
(1)Следует выделить область возмущения, до которой поток двигался со скоростью
с и после которой будет двигаться с такой же скоростью . Передняя критическая точка — это та точка, в которой поток встречается с поверхностью (по нормали к ней) и делится на две части, которые уходят вверх и вниз. Обе части сходятся в задней критической точке , так как поток неразрывный. Соединившись, поток должен вернуться в исходное по высоте место. Пройденный потоком путь от передней критической точки до задней критической точки по верхней плоскости lв значительно больше, чем по задней lн. Значит скорость прохождения сверху больше, а статическое давление меньше, чем внизу и в набегающем потоке.
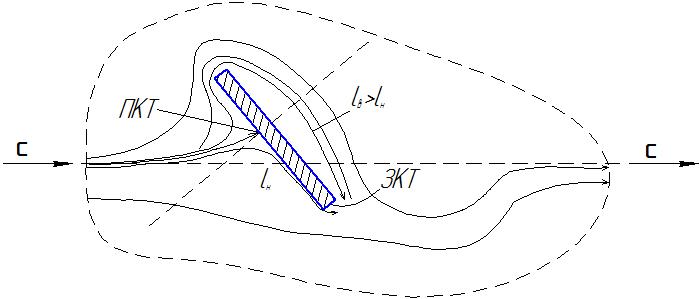
Рис. 5. Схема разделения потока при угле атаки меньше критического

Реальная картина распределения давлений изображено на рис. 8. Сверху и снизу пластины имеются области повышенного давления и области разряжения. Под действием этих перепадов давления появляется крутящий момент, стремящийся повернуть препятствие по часовой стрелке. На большей части верхней поверхности результирующее давление будет ниже атмосферного на величину динамического:
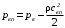 (2)
(2)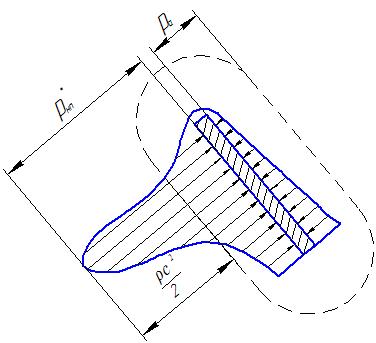
Рис.8. Реальная картина распределения давления
Для упрощения решения необходимо усреднить значение давления торможения на поверхностях пластины и пренебречь перепадом давления на верхней грани, но учесть снизу, таким образом:
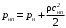 ; (3)
; (3)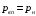 . (4)
. (4)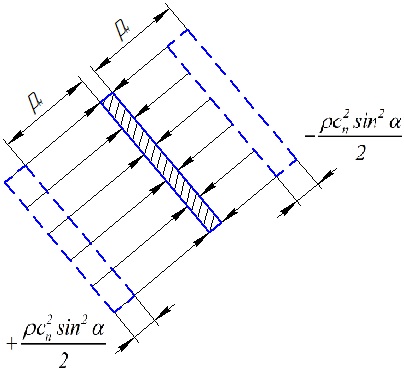
Рис. 7. Усредненное распределение давления
2.МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
2.1 Общее решение
Аэродинамическая сила, действующая на пластину, равна произведению перепада давлений на верхней и нижней гранях пластины на площадь рассматриваемого участка:
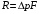 , (5)
, (5)где F – площадь рассматриваемой пластинки .