Файл: Пермский национальный исследовательский политехнический университет.docx
Добавлен: 10.01.2024
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
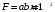 . (6)
. (6)Разность давлений верхней и нижней граней пластины:
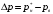 , (7)
, (7)где, согласно уравнению Бернулли:
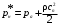 (8)
(8)cn = cнn. (9)
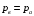 . (10)
. (10)Нормальная составляющая скорости невозмущённого потока равна произведению скорости невозмущённого потока на синус угла атаки:
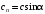 . (11)
. (11)Сила сопротивления и подъёмная сила соответственно равны:
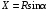 ; (12)
; (12)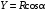 . (13)
. (13)Итак, выражение (5) имеет окончательный вид :
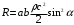 . (14)
. (14)В преобразованном виде (14) можно выделить коэффициент аэродинамической силы:
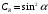 . (15)
. (15)Также можно записать выражения для сил сопротивления и подъемной силы, учитывая (14):
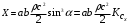 ; (16)
; (16)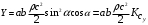 . (17)
. (17)В данных выражениях поправочные коэффициенты соответственно равны :
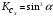 ; (18)
; (18) 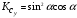 . (19)
. (19)Нужно сказать, что представленная модель для расчёта сил учитывает только влияние угла атаки на нормальную составляющую скорости, т.е. на давление частичного торможения. Но она не учитывает различные завихрения, неравномерность распределения по площади давлений и температур. Следовательно, она подходит только для физических моделей с углом атаки от 0 до некоторого критического значения.
2.2 Частное решение
Поскольку для рассмотрения была выбрана физическая модель пластины, угол атаки к которой принадлежит интервалу от 0º до 90º не включительно, то нужно найти значения полной аэродинамической силы для этого диапазона угла атаки.
Следует принять нормальные условия для высоты H=0 м согласно международной стандартной атмосфере:
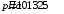 ; (20.1)
; (20.1)
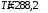
; (20.2)
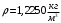 . (20.3)
. (20.3)Для упрощения математической модели, газ считали несжимаемым. В воздухе сжимаемость необходимо учитывать при скоростях v > 100 м/сек, которым соответствует число М > 0,3. Соответственно, следует взять число Маха меньше 0,3. Пусть М=0,25.
Так как число Маха представляет собой отношение скорости течения с в данной точке газового потока к местной скорости распространения звука a в движущейся среде. Согласно нормальным условиям для высоты H=0 м местная скорость распространения звука равна:
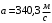 . (20.4)
. (20.4)Соответственно, предельная скорость течения будет равна:
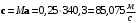 . (21)
. (21) Значение полной аэродинамической силы для угла атаки
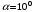 :
: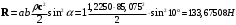 . (22)
. (22)Значение силы сопротивления для угла атаки
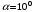 :
: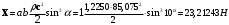 . (23)
. (23)Значение подъемной силы для угла атаки
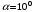 :
: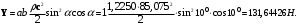 (24)
(24)Проверка:
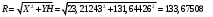 . (25)
. (25)Результаты расчетов для разных углов атаки отображены в диаграмме (рис.9):
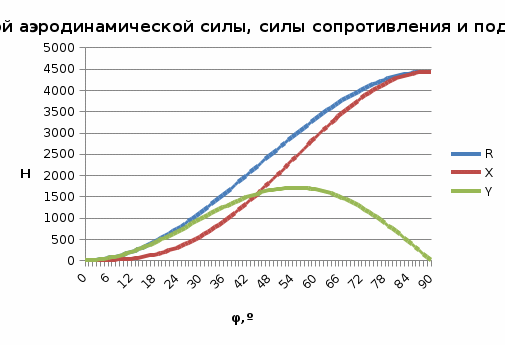
Рис.9.Графики зависимости полной аэродинамической силы, силы сопротивления и подъемной силы от угла атаки
3.АНАЛИЗ
С ростом угла атаки, как и ожидалось, аэродинамическая сила увеличивается, а её направление изменяется, что можно наблюдать из соотношения X и Y. Сила R в диапазоне углов от нуля до 25…30° возрастает по параболе, затем следует рост по линейному закону до 60°. Сила сопротивления X растёт по тому же принципу, но с некоторым запозданием, а при углах близких к 90° практически совпадает с аэродинамической силой. Значение подъёмной силы
Y до углов α = 20° практически совпадает со значением R. При дальнейшем увеличении угла атаки Yвозрастает, пока не достигнет своего максимума, критической точки, после чего её величина резко падает. Угол атаки, при котором подъемная сила достигает своего максимума, а после которого начинает уменьшаться, называется критическим углом. Соответственно, для данной физической модели критический угол получился равным 55º (см. таб.1 в приложении). При достижении критических углов атаки, плавное обтекание профиля пластины нарушается, появляется срыв потока, в результате чего подъёмная сила крыла резко уменьшается. И полученное решение не может быть использовано.
ЗАКЛЮЧЕНИЕ
В ходе проделанной работы были выполнены все поставленные задачи.
Выводы
Таким образом, с помощью простых математических вычислений были получены приблизительные данные о зависимости полной аэродинамической силы, подъемной силы, силы сопротивления от угла атаки. Такие расчеты не пригодны для реальных конструкторских расчетах, так как было принято много упрощений. Самую большую ошибку даёт отброс потери энергии на образование турбулентных вихрей.
Область применимости данной задачи ограничивается расчетами каких-либо плоских конструкций, работающих в условиях сильных воздушных возмущений. Так как было сказано о том, что составить математическую модель для случаев срыва потока довольно сложно, следует упомянуть, что данное решение пригодно для углов атаки меньше 55º.
Приложение
Таблица 1
Результаты расчёта аэродинамической силы, силы сопротивления и подъемной силы при предельной скорости потока c для разных углов атаки
| Угол атаки α,º | Аэродинамическая сила R | Сила сопротивления X | Подъемная сила Y |
| 0 | 0 | 0 | 0 |
| 1 | 1,35027 | 0,023565 | 1,350064 |
| 2 | 5,399435 | 0,188438 | 5,396146 |
| 3 | 12,14256 | 0,635493 | 12,12592 |
| 4 | 21,57144 | 1,504747 | 21,51889 |
| 5 | 33,67457 | 2,934932 | 33,54643 |
| 6 | 48,43721 | 5,063067 | 48,17187 |
| 7 | 65,84138 | 8,024046 | 65,35061 |
| 8 | 85,86588 | 11,95022 | 85,03024 |
| 9 | 108,4863 | 16,971 | 107,1507 |
| 10 | 133,6751 | 23,21243 | 131,6443 |
| 11 | 161,4015 | 30,79687 | 158,4361 |
| 12 | 191,6319 | 39,84251 | 187,4443 |
| 13 | 224,3293 | 50,46312 | 218,5798 |
| 14 | 259,454 | 62,7676 | 251,7471 |
| 15 | 296,9631 | 76,8597 | 286,8443 |
| 16 | 336,8109 | 92,83767 | 323,7634 |
| 17 | 378,9489 | 110,7939 | 362,3907 |
| 18 | 423,3258 | 130,8149 | 402,6068 |
| 19 | 469,8874 | 152,9804 | 444,2873 |
| 20 | 518,5772 | 177,3638 | 487,3031 |
| 21 | 569,3356 | 204,0316 | 531,5206 |
| 22 | 622,1009 | 233,0431 | 576,8019 |
| 23 | 676,8089 | 264,4503 | 623,0058 |
| 24 | 733,3927 | 298,2977 | 669,9876 |
| 25 | 791,7836 | 334,6222 | 717,5997 |
| 26 | 851,9104 | 373,4529 | 765,692 |
| 27 | 913,6998 | 414,811 | 814,1125 |
| 28 | 977,0766 | 458,7097 | 862,7074 |
| 29 | 1041,963 | 505,1539 | 911,3217 |
| 30 | 1108,281 | 554,1407 | 959,7998 |
| 31 | 1175,95 | 605,6588 | 1007,985 |
| 32 | 1244,886 | 659,6888 | 1055,723 |
| 33 | 1315,005 | 716,2033 | 1102,856 |
| 34 | 1386,224 | 775,1664 | 1149,232 |
| 35 | 1458,454 | 836,5346 | 1194,695 |
| 36 | 1531,607 | 900,2561 | 1239,096 |
| 37 | 1605,595 | 966,2713 | 1282,285 |
| 38 | 1680,328 | 1034,513 | 1324,116 |
| 39 | 1755,713 | 1104,906 | 1364,446 |
| 40 | 1831,661 | 1177,369 | 1403,133 |
| 41 | 1908,077 | 1251,811 | 1440,044 |
| 42 | 1984,869 | 1328,136 | 1475,045 |
| 43 | 2061,943 | 1406,242 | 1508,01 |
| 44 | 2139,206 | 1486,017 | 1538,816 |
| 45 | 2216,563 | 1567,346 | 1567,346 |
| 46 | 2293,92 | 1650,108 | 1593,49 |
| 47 | 2371,182 | 1734,173 | 1617,142 |
| 48 | 2448,257 | 1819,409 | 1638,203 |
| 49 | 2525,049 | 1905,678 | 1656,581 |
| 50 | 2601,465 | 1992,838 | 1672,189 |
| 51 | 2677,412 | 2080,74 | 1684,95 |
| 52 | 2752,798 | 2169,234 | 1694,791 |
| 53 | 2827,53 | 2258,166 | 1701,65 |
| 54 | 2901,518 | 2347,378 | 1705,47 |
| 55 | 2974,672 | 2436,708 | 1706,202 |
| 56 | 3046,902 | 2525,996 | 1703,806 |
| 57 | 3118,12 | 2615,075 | 1698,25 |
| 58 | 3188,24 | 2703,781 | 1689,51 |
| 59 | 3257,176 | 2791,945 | 1677,57 |
| 60 | 3324,844 | 2879,399 | 1662,422 |
| 61 | 3391,162 | 2965,977 | 1644,068 |
| 62 | 3456,049 | 3051,51 | 1622,517 |
| 63 | 3519,426 | 3135,831 | 1597,786 |
| 64 | 3581,215 | 3218,775 | 1569,901 |
| 65 | 3641,342 | 3300,176 | 1538,897 |
| 66 | 3699,733 | 3379,874 | 1504,817 |
| 67 | 3756,316 | 3457,708 | 1467,71 |
| 68 | 3811,024 | 3533,52 | 1427,635 |
| 69 | 3863,79 | 3607,158 | 1384,658 |
| 70 | 3914,548 | 3678,472 | 1338,854 |
| 71 | 3963,238 | 3747,315 | 1290,304 |
| 72 | 4009,8 | 3813,546 | 1239,096 |
| 73 | 4054,176 | 3877,028 | 1185,326 |
| 74 | 4096,314 | 3937,63 | 1129,097 |
| 75 | 4136,162 | 3995,226 | 1070,518 |
| 76 | 4173,671 | 4049,695 | 1009,702 |
| 77 | 4208,796 | 4100,925 | 946,7731 |
| 78 | 4241,493 | 4148,807 | 881,8561 |
| 79 | 4271,724 | 4193,24 | 815,0833 |
| 80 | 4299,45 | 4234,132 | 746,5917 |
| 81 | 4324,639 | 4271,396 | 676,5226 |
| 82 | 4347,259 | 4304,952 | 605,0216 |
| 83 | 4367,284 | 4334,731 | 532,238 |
| 84 | 4384,688 | 4360,668 | 458,3247 |
| 85 | 4399,451 | 4382,71 | 383,4374 |
| 86 | 4411,554 | 4400,808 | 307,7344 |
| 87 | 4420,983 | 4414,924 | 231,3764 |
| 88 | 4427,726 | 4425,029 | 154,5254 |
| 89 | 4431,775 | 4431,1 | 77,34514 |
| 90 | 4433,125 | 4433,125 | 2,72E-13 |