Файл: Лабораторная работа 2 Проверила Мишура Людмила Геннадьевна Дата Оценка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего
образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИТМО»
Выполнили:
Студент группы U312121
Камышева Е.В.
Лабораторная работа №2
Проверила: Мишура Людмила Геннадьевна
Дата:
Оценка:
Специальность: 38.03.05 Бизнес-информатика
09.02.03 Программирование в компьютерных системах
Санкт-Петербург 2022
Исходные данные:
Данные о величинах суммарных активов и чистого дохода банков Японии в млн. долл. США.
| Данные о величинах суммарных активов и чистого дохода банков Японии, млн. долл. США | | | |||||||||||||
| | |||||||||||||||
| Суммарные активы | 507.2 | 506.6 | 487.8 | 496.6 | 458.1 | 429.3 | 486.9 | 311.5 | 302.2 | 386.9 | | | | ||
| Чистый доход | 6.92 | 7.12 | 6.73 | 6.1 | 4.96 | 4.62 | 5.11 | 3.3 | 1.8 | 4.5 | | | |||
Таблица 1. Исходные данные.
Выявление связи между признаками:
В данном случае суммарные активы это факторный признак, а чистый доход – результативный.
1.Построение точечной диаграммы корреляционного поля.
Построим точечную диаграмму корреляционного поля, исходя из табличных значений, где принимаем суммарные активы за результативный признак, а доход за факторный признак. (Рисунок 1).
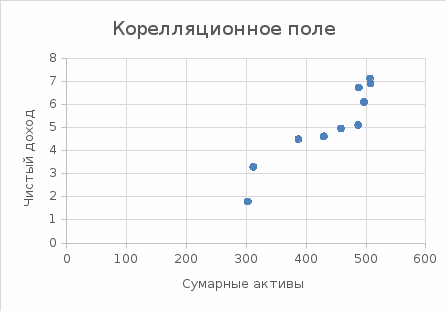
Рисунок 1. Точечная диаграмма корреляционного поля.
В расположении точек на диаграмме наблюдается определенная зависимость: точки на графике расположены примерно на линии вида
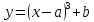. Визуально можно сказать, что между признаками существует связь, они не хаотично разбросаны по корреляционному полю.2. Проверка по результативному признаку на однородность и нормальность.
Используем результаты аналитической группировки для проверки единиц наблюдения по результативному признаку на однородность и нормальность.
Рассчитываем среднюю арифметическую проcтую
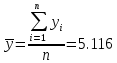.Рассчитываем дисперсию уровней динамического ряда и среднее квадратическое отклонение уровней по двум формулам:
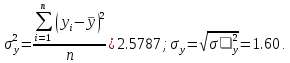
Теперь рассчитаем коэффициент вариации для факторного признака по формуле:
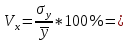31.4%<
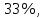следовательно, ряд считается однородным, колеблемость признака не высокая.Оценим нормальность совокупности. Для этого проверим выполнение правила «трех сигм» для факторного признака:
| 2. Проверка распределения на нормальность (правило 3-х сигм) | ||||
| Начало и конец интервала | Число единиц попадающих в интервал | Удельный вес единиц, попавших в интервал, % | ||
| yср ± σ | 3.51 | 6.72 | 5 | 50% |
| yср ± 2σ | 1.90 | 8.33 | 9 | 90% |
| yср ± 3σ | 0.30 | 9.93 | 10 | 100% |
Таблица 2. Нормальность распределения.
В распределении есть незначительные отклонения от нормального. Аномальных значений в первичной информации нет.
3. Описание связи в табличной форме.
Представим выявленную связь в табличном виде. Для этого проранжируем совокупность по факторному признаку(суммарные активы). (Таблица 3).
| Ранжированная совокупность по факторному признаку. | | | ||||||||||||
| | ||||||||||||||
| Суммарные активы | 302.2 | 311.5 | 386.9 | 429.3 | 458.1 | 486.9 | 487.8 | 496.6 | 506.6 | 507.2 | | | ||
| Чистый доход | 1.8 | 3.3 | 4.5 | 4.62 | 4.96 | 5.11 | 6.73 | 6.1 | 7.12 | 6.92 | | | ||
Таблица 3. Проранжированная таблица по факторному признаку.
4. Описание связи в графической форме.
Далее нам следует представить связь в графическом виде. Построим линию эмпирической регрессии, где абсцисса – факторный признак, а ордината – результативный. Полученный рафик, можно увидеть на рисунке 2.
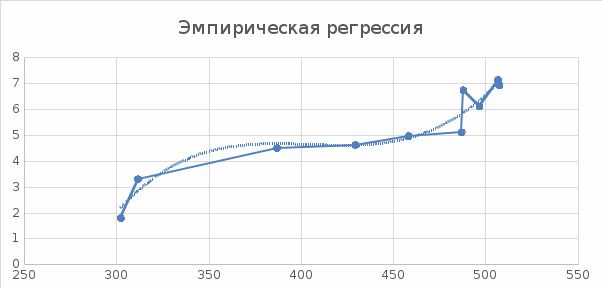
Рисунок 2. Линия эмпирической регрессии.
Таким образом, мы получили ломанную линию, отражающую основную тенденцию рассматриваемой зависимости.
5. Описание связи в аналитической форме.
Далее нам необходимо представить связь в аналитическом виде
. Для этого нам нужно построить несколько различных корреляционных моделей, используя разные математические функции. Подбор функции осуществляется на основе анализа эмпирической линии регрессии. Проанализировав ее, мы можем предположить, что справедливо построить линейную и параболическую функцию.
Параметры модели рассчитываются с использованием метода наименьших квадратов:
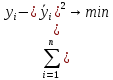. Для начала рассчитаем линейный коэффициент корреляции, что бы установить наличие связи между факторными и результативными признаками:
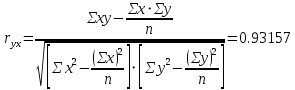. Оценка производится по шкале Чеддока: 
По ней можно сделать вывод, что тесноту связи между суммарными активами и чистым заработком, можно считать сильной.
5.1 Линейная зависимость.
Поэтому первую математическую модель для построения уравнения парной регрессии выберем линейную. Она имеет вид : полинома первой степени:
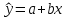. Для нахождения численных значений параметров a и b мы воспользуемся методом наименьших квадратов, используя систему нормальных уравнений: 
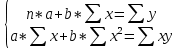, отсюда получаем, что a = -3.6788 и b = 0.02011. Уравнение имеет вид: 
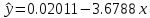. Интерпретируем модель. Коэффициент b – коэффициент регрессии. Он положительный, значит кривая графика функции стремится вверх, то есть при увеличении факторного признака увеличивается результативный признак.
Далее нам необходимо оценить существенность корреляционной связи, получившейся линейной модели. Мы можем это сделать с помощью t-критерия Стьюдента:
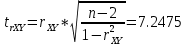. Критическое значение t-критерия Стьюдента 
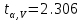, при уровне значимости α=0.05 и числе степеней свободы вариации V=10-2=8. 
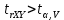, следовательно связь между результативным и факторным признаками признается достоверной, а построенная модель - надежной. Далее нам необходимо посчитать остаточную дисперсию по формуле
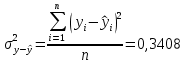. Оценим тесноту связи по теоретическим данным. Для линейной модели рассчитаем по формуле: 
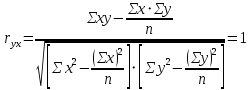.Результаты вычисления можно увидеть в таблице 4, а изображение зависимости на рисунке 3.
Т
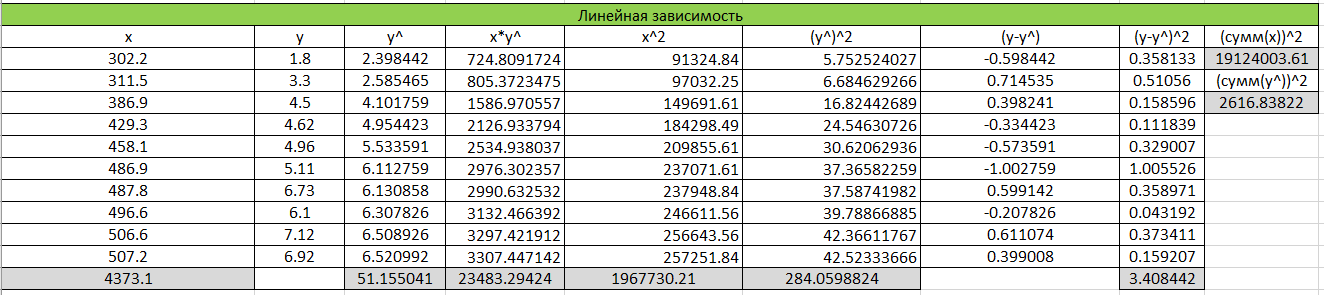аблица 4. Линейная зависимость.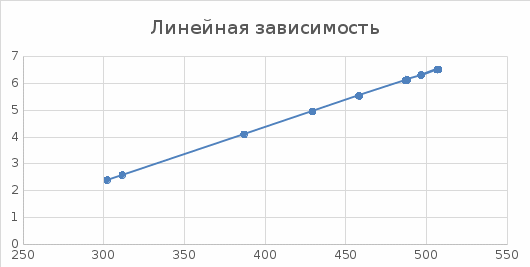
Рисунок 3. Линейная зависимость.
По полученным теоретическим данным связь между активами и объемами продаж предприятий получилась функциональная.
5.2 Полином третьей степени.
Построим вторую математическую функцию для уравнения парной регрессии. Теперь это будет функция - полином третьей степени:
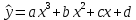. Система нормальных уравнений для нахождения параметров имеет вид: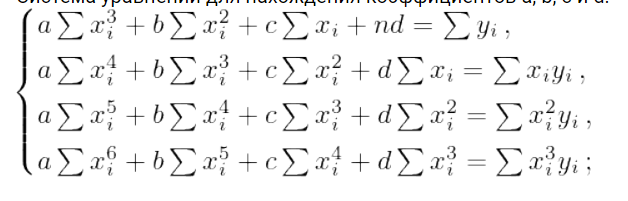
Получились такие коэффициенты: a=2.49953*10^(-6); b= -0.0030; c= 1.2281; d= -160.5081.
Таким образом полученное уравнение:
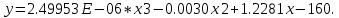81. Расчеты для полинома можно увидеть в таблице 5.
Таблица 5. Расчеты для полинома третьей степени.
Далее мы рассчитали остаточную дисперсию, по соответствующей формуле:
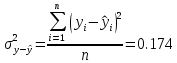. Все расчеты можно найти в таблице 6, получившуюся функцию на рисунке 4.| x | y | y^ | (y-y^)^2 | x*y^ | x^2 | (y^)^2 |
| 302.20 | 1.80 | 2.177675429 | 0.14263873 | 658.0935147 | 91324.84 | 4.742270275 |
| 311.50 | 3.30 | 2.827790921 | 0.222981414 | 880.8568719 | 97032.25 | 7.996401493 |
| 386.90 | 4.50 | 4.670856207 | 0.029191844 | 1807.154267 | 149691.61 | 21.81689771 |
| 429.30 | 4.62 | 4.613231319 | 4.5815E-05 | 1980.460205 | 184298.49 | 21.28190321 |
| 458.10 | 4.96 | 4.876324137 | 0.00700165 | 2233.844087 | 209855.61 | 23.77853709 |
| 486.90 | 5.11 | 5.7985631 | 0.474119143 | 2823.320374 | 237071.61 | 33.62333403 |
| 487.80 | 6.73 | 5.841912603 | 0.788699225 | 2849.684968 | 237948.84 | 34.12794286 |
| 496.60 | 6.10 | 6.320387603 | 0.048570696 | 3138.704484 | 246611.56 | 39.94729945 |
| 506.60 | 7.12 | 6.993648569 | 0.015964684 | 3542.982365 | 256643.56 | 48.91112031 |
| 507.20 | 6.92 | 7.038734919 | 0.014097981 | 3570.046351 | 257251.84 | 49.54378926 |
| 4373.1 | | 51.15912481 | 1.743311182 | 23485.14749 | 1967730.21 | 285.7694957 |