Таблица 6. Расчеты для полинома третьей степени.



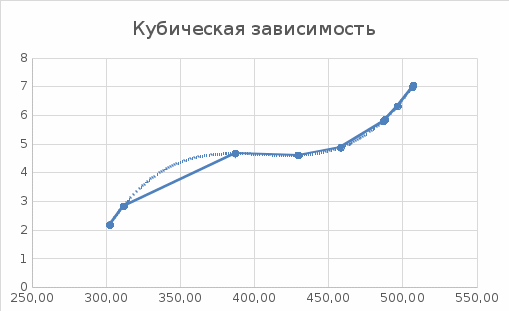
Рисунок 4. Кубическая зависимость.

Давайте проверим существенность связи через F-критерий. Для начала нам надо найти фактическое значение F-критерия, мы делаем это по формуле: 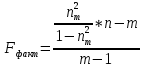, где теоретический коэффициент детерминации, определяется по формуле: 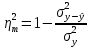. . 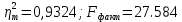Далее нам необходимо найти критическое значение критерия Фишера. Оно равно 4.76, при α=0,05 и числе степеней свободы V1=3, V2=10-4=6. 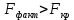, следовательно связь можно считать надежной и достоверной.

Оценим тесноту связи для теоретических данных, с помощью множественного коэффициента корреляции – R, 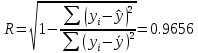, по шкале Чеддока связь считается значимой.

6. Сравним полученные модели.

Модель	Остаточная дисперсия	Коэффициенты тесноты	t-критерий / F-критерий
Линейная	0,3408	1	7,24
Полином третей степени	0,174	0,9656	27,584

Анализируя полученную таблицу отдаем предпочтению, графику модели полиному третьей степени.

7. Вывод.

В ходе работы мы построили и проанализировали корреляционное поле, определили, что между признаками существует связь, так как точки с координатами признаков не хаотично разбросаны по корреляционному полю. Рассчитав коэффициент вариации для факторного признака, убедились, что наша совокупность является однородной. Затем оценили нормальность совокупности проверив выполнение правила «трех сигм» для факторного признака. Удалось заметить, что в совокупности отсутствуют аномальные значения, распределение значений не отклоняется от нормы.

Далее представили выявленную связь в табличном виде (для этого упорядочили совокупность по факторному признаку (суммарные активы)) и графическом виде (построили линию эмпирической регрессии, где абсцисса – факторный признак, ордината – результативный.). Результат графического представления - ломанная линия, отражающая основную тенденцию рассматриваемой зависимости.

---

Мы рассчитали линейный коэффициент корреляции (он получился положительным, значит связь прямая – при увеличении зарплат в регионах увеличивается и прожиточный минимум, и наоборот, при этом в линейной модели эта зависимость высокая), оценили его по шкале Чеддока и сделали вывод, что теснота связи высокая. (0,94 ∈[0,91;0,99]).

Затем построили линейную математическую модель для уравнения парной регрессии и оценили существенность парной корреляционной связи, получившейся линейной модели с помощью критерия Стьюдента.( trXY>t(α,V), следовательно модель признается значимой).

Построили вторую математическую модель для построения уравнения парной регрессии (полином третьей степени) и воспользовались критерием Фишера для определения ее надёжности. (Fфакт>Fкр), следовательно корреляционная модель признается надежной).

Мы отдали предпочтение кубической модели, потому что у данной модели все показатели выше, чем у линейной, кроме тесноты связи, но различие незначительное.

---

Смотрите также файлы

• Рассказать свои стихи Мы уже настроились. Я проснулся очень рано, Поскорее встал с дивана, Умывался, наряжался.docx

• Что такое seo и зачем это фрилансерам.docx

• Урока Тема занятия Критерий оценки.docx

• 4. Общие проблемы малой группы. Динамические процессы в малой группе. Развитие малой группы. Прочитайте случаи, найдите в них один или несколько законов социальной психологии (групповые эффекты), объясните, какие фразы в тексте говорят об этом, а так же п.docx

• Занятие для обучающихся 57 классов по теме 110 лет со дня рождения советского писателя и поэта, автора слов гимна ссср и гимна россии с. В. Михалкова.doc