Файл: Пояснительная записка Предмет Теоретическая и прикладная механика Тема курсовой работы Кинематическое исследование механизмов Автор работы Наурзалиев Ерлан Бержанович.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 . Из чертежа измеряем отрезки и вычисляем (в числовом выражении) скорости
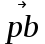 =75 мм ,
=75 мм , 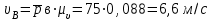
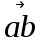 = 55 мм ,
= 55 мм , 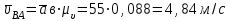
На плане скоростей:
вектор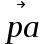 условно изображает абсолютную скорость точки А (VА = 6,6 м/с); вектор
условно изображает абсолютную скорость точки А (VА = 6,6 м/с); вектор 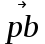 условно изображает абсолютную скорость точки В - (VВ = 6,6 м/с);
условно изображает абсолютную скорость точки В - (VВ = 6,6 м/с);
вектор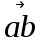 условно изображает относительную скорость точки В относительно точки А- (VВА = 4,84 м/с);
условно изображает относительную скорость точки В относительно точки А- (VВА = 4,84 м/с);
Вектора проходящие через полюс называются абсолютными, а не проходящие через полюс - относительными.
Определяем угловую скорость 2 звена (АВ), т.е. шатуна

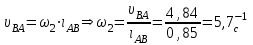
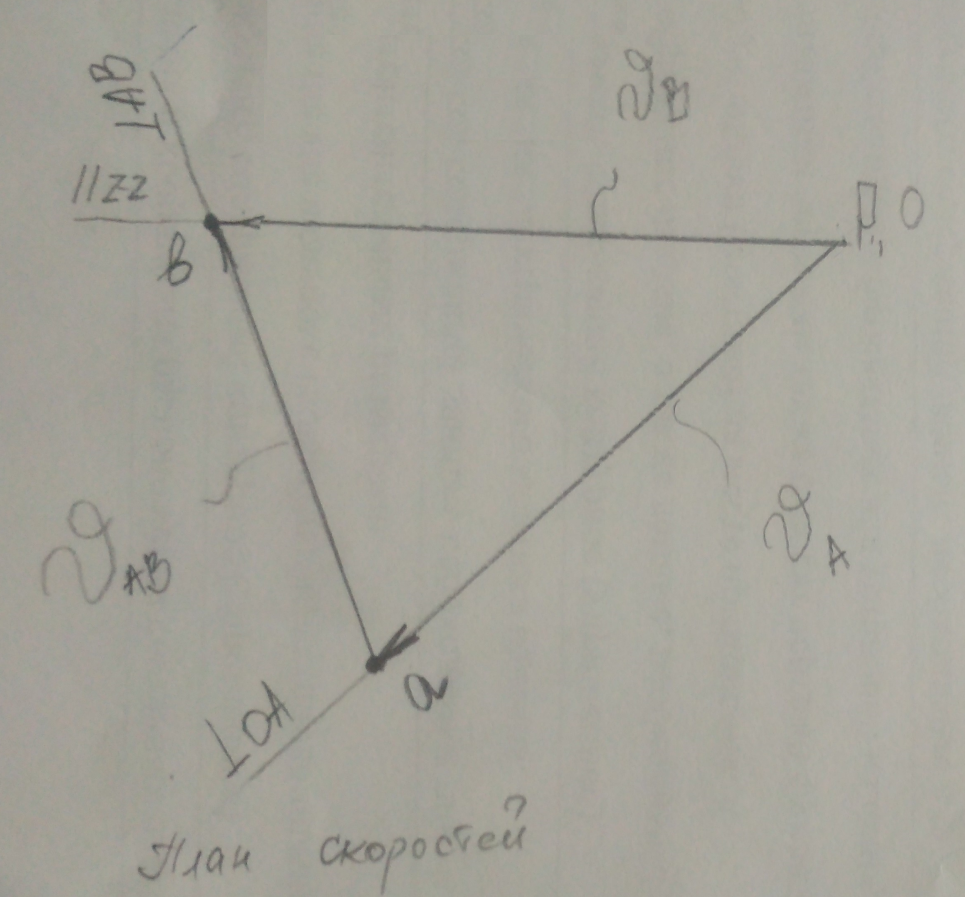
Рис.4 – План скоростей
Строим план ускорений.
Определяем ускорение точки А через известное ускорение точки О. Запишем векторное уравнение для первого звена. (см. Рис.5).
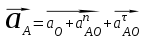 ,
,
где: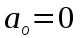 ,
,
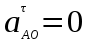 , т.к. ω1 = const., т.е. ε=0 тогда векторное уравнение примет вид:
, т.к. ω1 = const., т.е. ε=0 тогда векторное уравнение примет вид:
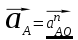
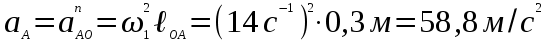
Выбираем масштаб ускорений:
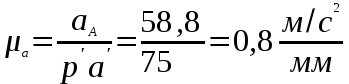
Выбираем произвольную точку р/ – полюс плана ускорений. От точки p/ проводим линию параллельную // к АО в сторону направления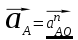 ускорения и на ней отложим вектор
ускорения и на ней отложим вектор 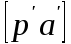 = 75 мм. (выбираем произвольно). Вектор p/a/ условно изображает абсолютное ускорение точки А (
= 75 мм. (выбираем произвольно). Вектор p/a/ условно изображает абсолютное ускорение точки А (
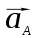 );
);
Определяем ускорение точки В через известное ускорение точки А.
Для этого напишем векторное уравнение для второго звена :
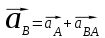
где: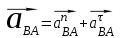 , тогда векторное уравнение примет вид:
, тогда векторное уравнение примет вид:
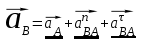
В этом уравнении ускорение точки А подчеркиваем дважды, так как оно известно нам в числовом значении и по направлению.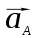 направлено параллельно звену ОА в направлении от точки А к точке О (к центру вращения). Звено АВ совершает сложное движение (плоскопараллельное), а в относительном движении т.В вращается вокруг т.А.
направлено параллельно звену ОА в направлении от точки А к точке О (к центру вращения). Звено АВ совершает сложное движение (плоскопараллельное), а в относительном движении т.В вращается вокруг т.А.
Нормальное ускорение точки В относительно точки А известно также дважды: в числовом выражении и по направлению.
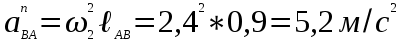

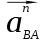 направлено параллельно звену АВ в направлении от точки В к точке А.
направлено параллельно звену АВ в направлении от точки В к точке А.
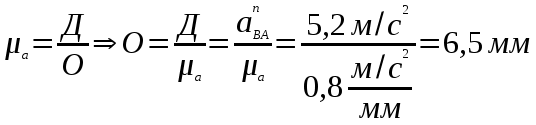 = а/n2
= а/n2
От т. а/ (черт.5) проводим линию перпендикулярную к АВ в сторону А (А- мгновенный центр вращения) и на ней отложим отрезок
а/n2 = 6,5 мм. (а/n2 - нормальное ускорение второго звена).

Через точку n2 проводим линию ┴ к АВ, так как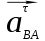 ┴
┴ 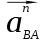 , а от точки р (полюса) проведем параллельную линию к оси Z-Z. На пересечении двух линий находим искомую точку b/. При построении получаем четырехугольник p/ а/ n2 b/ , который называется планом ускорения. Из чертежа измеряем полученные отрезки
, а от точки р (полюса) проведем параллельную линию к оси Z-Z. На пересечении двух линий находим искомую точку b/. При построении получаем четырехугольник p/ а/ n2 b/ , который называется планом ускорения. Из чертежа измеряем полученные отрезки
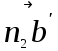 = 68мм ,
= 68мм ,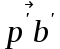 = 17мм
= 17мм
Соединяем а/ в/ и определяем графически.
Вектор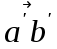 = 68мм изображает полное относительное ускорение.
= 68мм изображает полное относительное ускорение.
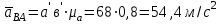
Вектор условно изображает абсолютное ускорение т.В
условно изображает абсолютное ускорение т.В
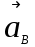 =
=  ∙µа = 17 мм · 0.8 = 13,6 м/с2;
∙µа = 17 мм · 0.8 = 13,6 м/с2;
Вектор условно изображает касательное ускорение звена (АВ)
условно изображает касательное ускорение звена (АВ) 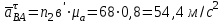
Положения точек S и С на плане ускорений определяются на основании теоремы подобия планов механизма и ускорений по следующим пропорциям:
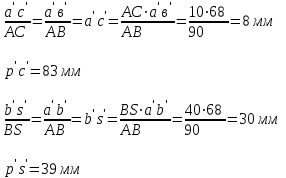
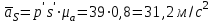
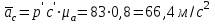
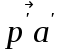 ,
,  ,
, 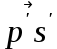 ,
, 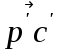 - абсолютная величина
- абсолютная величина
 - относительная величина
- относительная величина
Вектора проходящие через полюс (Р) называются абсолютными величинами, а не проходящие через полюс- относительными.
Угловое ускорение ε2 второго звена (АВ)
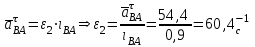
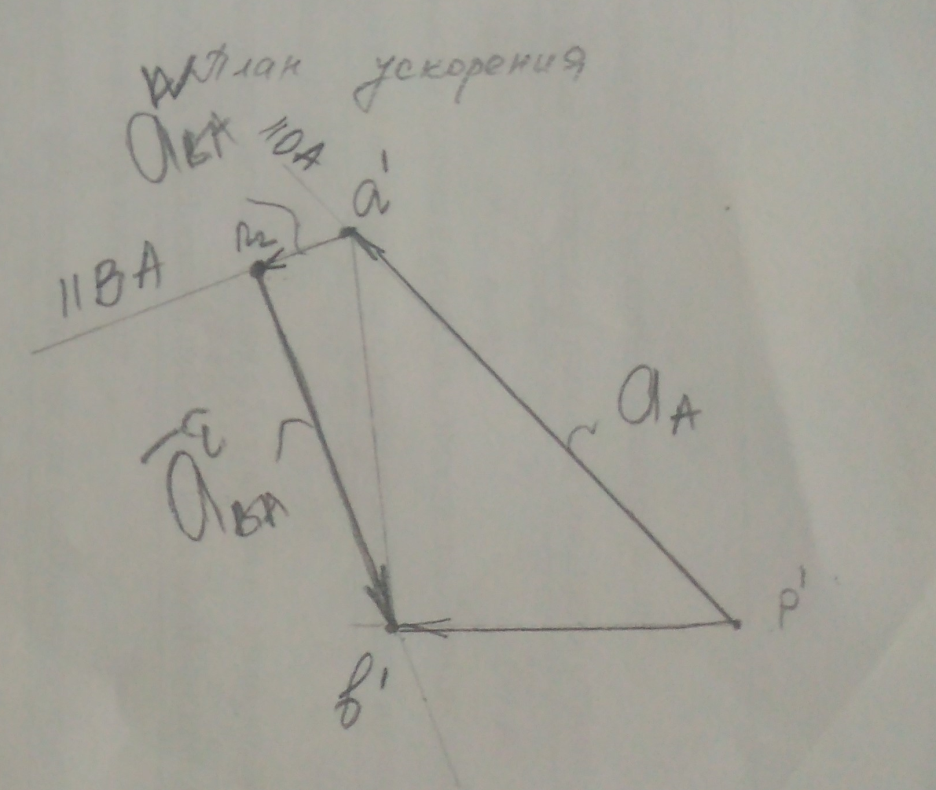
Рис.5 – План ускорения
Раздел 2 «Кинематическое исследование сложного кривошипно-шатунного механизма
2.1. Построение плана механизма
Для построения плана механизма необходимо выбрать масштаб μℓ.
С учетом размеров звеньев механизма выбираем масштаб длины μℓ= 0,005 м/мм.
Переведем все действительные размеры в масштабные по формуле:
 =
=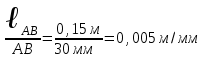



,
где: О – масштабная величина, мм; Д – действительная величина, м;
 - масштаб длины, м/мм.
- масштаб длины, м/мм.
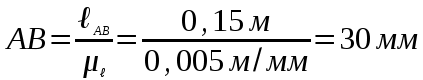 и т. д.
и т. д.
Все полученные величины занесем в таблицу 1.
Таблица 1
ω1=22 с-1
По приведенным данным таблицы 1 построим план механизма (см.Рис.1).
Выбираем произвольную т.О - начало координатных осей. Проводим горизонтальную ось ОХ и вертикальную ось ОУ. Радиусом АВ = 30 мм с
центром в т.А проводим окружность. Окружность является траекторией движения т. В при вращении.
С помощью циркуля окружность разделим на 12 равных частей и каждое деление отмечаем буквами ВО, В1, В2, В3, . . . . .В11, В12 (ВО);
На расстоянии [L1] от центра А и [L3] определяем положение неподвижной опоры ( точки D) . От точки D радиусом CD=90 мм чертим дугу , а от точки В радиусом ВС=90 мм чертим вторую дугу. При пересечении находим искомую точку С. Аналогично таким же методом находим 12 положений точки С: С0, С1, С2, С3, С4, С5, С6, С7, С8, С9
, С10, С11, С12 (С0).
Чтобы найти положение точки М, нужно от точки С радиусом СМ=40 мм и от точки D радиусом DM=70 мм чертим дуги. При пересечении двух дух находим положение точки М.
Затем от центра ,т.е точки А на расстоянии [L2]= 36 мм проводим вертикальный шток. При пересечении второго звена (АВ) соответственно нумеруем 12 положений точки Е : Е0, Е1, Е2, Е3, Е4, Е5, Е6, Е7, Е8, Е9, Е10, Е11, Е12 (Е0).
От каждой точки Е соответственно откладываем отрезок [EF]=60 мм и находим 12 положений точки F: F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12 (F0).
На вертикальном штоке измеряем расстояние от верхней, крайней точки до нижней ,крайней точки F (Рис.4, Чертеж 1).
F2 – F10 = Н- ход штока , F2 –нижняя , крайняя точка штока , а F10- верхняя, крайняя точка штока . F2- принимаем за начало отсчета. Из чертежа 1 измеряем расстояния,тогда
F2 F1=5мм
F2 F2=0мм
F2 F3=2мм
F2 F4=9 мм
F2 F5=12 мм
F2 F6=15мм
F2 F7=20 мм
F2 F8=28мм
F2 F9=36мм
F2 F10=40мм
F2 F11=32мм
F2 F12=19мм
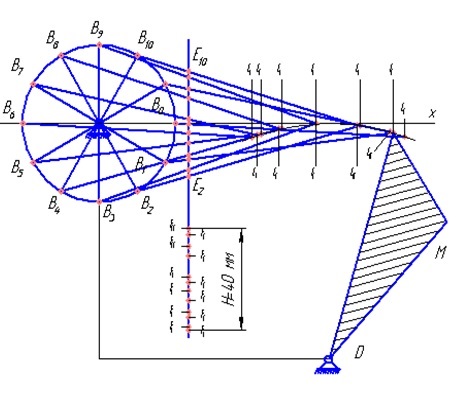
Рис.1 – Траектория точек В,С,Е,F
2.1.Построение диаграммы перемещения штока
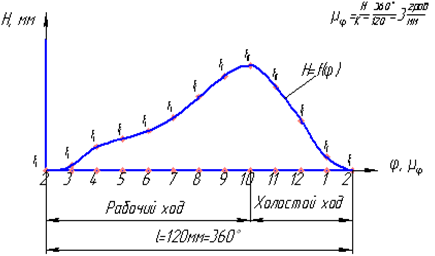
При одном полном обороте перемещение ползуна изменяется. И это изменение мы должны показать на диаграмме. Чтобы построить диаграмму нужно определить масштаб угла

Построим прямоугольную систему координат ХОУ(φОН). φ- угол поворота кривошипа; Н-ход ползуна; т.О- начало координат.
По горизонтальной оси откладываем отрезок L=120 мм, условно изображающий 360о, т.е. один полный оборот кривошипа.
Отрезок L разделим на 12 равных частей и тогда каждое деление условно изображает 30о угла поворота кривошипа.
По вертикальной оси откладываем величины: В0В1...В0В12. Полученные точки соединяем плавной кривой.
Таким образом получим диаграмму перемещения ползуна в зависимости от угла поворота кривошипа . Это кривая математически выражается Н=f(φ). (см.Рис.2)
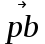 =75 мм ,
=75 мм , 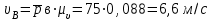
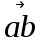 = 55 мм ,
= 55 мм , 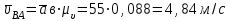
На плане скоростей:
вектор
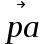 условно изображает абсолютную скорость точки А (VА = 6,6 м/с); вектор
условно изображает абсолютную скорость точки А (VА = 6,6 м/с); вектор 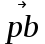 условно изображает абсолютную скорость точки В - (VВ = 6,6 м/с);
условно изображает абсолютную скорость точки В - (VВ = 6,6 м/с);вектор
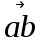 условно изображает относительную скорость точки В относительно точки А- (VВА = 4,84 м/с);
условно изображает относительную скорость точки В относительно точки А- (VВА = 4,84 м/с); Вектора проходящие через полюс называются абсолютными, а не проходящие через полюс - относительными.
Определяем угловую скорость 2 звена (АВ), т.е. шатуна

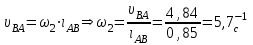

Рис.4 – План скоростей
-
1.5.Построение планов ускорений
Строим план ускорений.
Определяем ускорение точки А через известное ускорение точки О. Запишем векторное уравнение для первого звена. (см. Рис.5).
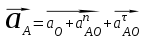 ,
, где:
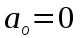 ,
, 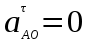 , т.к. ω1 = const., т.е. ε=0 тогда векторное уравнение примет вид:
, т.к. ω1 = const., т.е. ε=0 тогда векторное уравнение примет вид: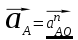
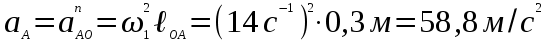
Выбираем масштаб ускорений:
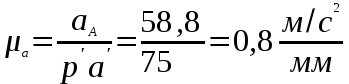
Выбираем произвольную точку р/ – полюс плана ускорений. От точки p/ проводим линию параллельную // к АО в сторону направления
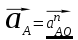 ускорения и на ней отложим вектор
ускорения и на ней отложим вектор 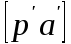 = 75 мм. (выбираем произвольно). Вектор p/a/ условно изображает абсолютное ускорение точки А (
= 75 мм. (выбираем произвольно). Вектор p/a/ условно изображает абсолютное ускорение точки А (
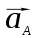 );
);Определяем ускорение точки В через известное ускорение точки А.
Для этого напишем векторное уравнение для второго звена :
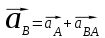
где:
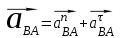 , тогда векторное уравнение примет вид:
, тогда векторное уравнение примет вид: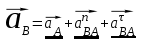
В этом уравнении ускорение точки А подчеркиваем дважды, так как оно известно нам в числовом значении и по направлению.
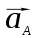 направлено параллельно звену ОА в направлении от точки А к точке О (к центру вращения). Звено АВ совершает сложное движение (плоскопараллельное), а в относительном движении т.В вращается вокруг т.А.
направлено параллельно звену ОА в направлении от точки А к точке О (к центру вращения). Звено АВ совершает сложное движение (плоскопараллельное), а в относительном движении т.В вращается вокруг т.А. Нормальное ускорение точки В относительно точки А известно также дважды: в числовом выражении и по направлению.
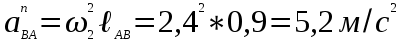

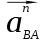 направлено параллельно звену АВ в направлении от точки В к точке А.
направлено параллельно звену АВ в направлении от точки В к точке А.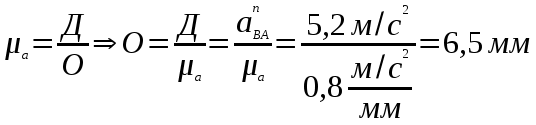 = а/n2
= а/n2От т. а/ (черт.5) проводим линию перпендикулярную к АВ в сторону А (А- мгновенный центр вращения) и на ней отложим отрезок
а/n2 = 6,5 мм. (а/n2 - нормальное ускорение второго звена).

Через точку n2 проводим линию ┴ к АВ, так как
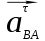 ┴
┴ 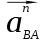 , а от точки р (полюса) проведем параллельную линию к оси Z-Z. На пересечении двух линий находим искомую точку b/. При построении получаем четырехугольник p/ а/ n2 b/ , который называется планом ускорения. Из чертежа измеряем полученные отрезки
, а от точки р (полюса) проведем параллельную линию к оси Z-Z. На пересечении двух линий находим искомую точку b/. При построении получаем четырехугольник p/ а/ n2 b/ , который называется планом ускорения. Из чертежа измеряем полученные отрезки 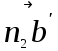 = 68мм ,
= 68мм ,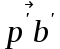 = 17мм
= 17мм Соединяем а/ в/ и определяем графически.
Вектор
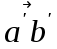 = 68мм изображает полное относительное ускорение.
= 68мм изображает полное относительное ускорение.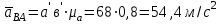
Вектор
 условно изображает абсолютное ускорение т.В
условно изображает абсолютное ускорение т.В 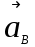 =
=  ∙µа = 17 мм · 0.8 = 13,6 м/с2;
∙µа = 17 мм · 0.8 = 13,6 м/с2; Вектор
 условно изображает касательное ускорение звена (АВ)
условно изображает касательное ускорение звена (АВ) 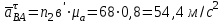
Положения точек S и С на плане ускорений определяются на основании теоремы подобия планов механизма и ускорений по следующим пропорциям:
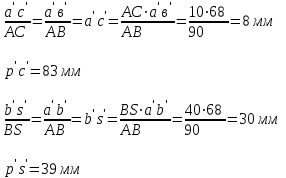
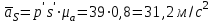
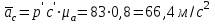
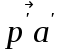 ,
,  ,
, 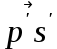 ,
, 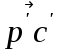 - абсолютная величина
- абсолютная величина - относительная величина
- относительная величинаВектора проходящие через полюс (Р) называются абсолютными величинами, а не проходящие через полюс- относительными.
Угловое ускорение ε2 второго звена (АВ)
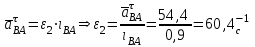

Рис.5 – План ускорения
Раздел 2 «Кинематическое исследование сложного кривошипно-шатунного механизма
2.1. Построение плана механизма
Для построения плана механизма необходимо выбрать масштаб μℓ.
С учетом размеров звеньев механизма выбираем масштаб длины μℓ= 0,005 м/мм.
Переведем все действительные размеры в масштабные по формуле:
 =
=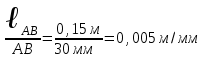



,
где: О – масштабная величина, мм; Д – действительная величина, м;
 - масштаб длины, м/мм.
- масштаб длины, м/мм.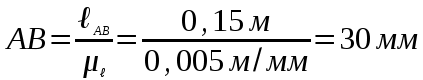 и т. д.
и т. д.Все полученные величины занесем в таблицу 1.
Таблица 1
| Действительная величина,м | |
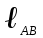 | 0,15 |
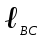 = =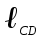 | 0,45 |
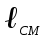 | 0,2 |
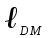 | 0,35 |
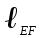 | 0,3 |
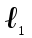 = =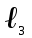 | 0,45 |
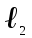 | 0,18 |
| φ | 650 |
ω1=22 с-1
По приведенным данным таблицы 1 построим план механизма (см.Рис.1).
Выбираем произвольную т.О - начало координатных осей. Проводим горизонтальную ось ОХ и вертикальную ось ОУ. Радиусом АВ = 30 мм с
центром в т.А проводим окружность. Окружность является траекторией движения т. В при вращении.
С помощью циркуля окружность разделим на 12 равных частей и каждое деление отмечаем буквами ВО, В1, В2, В3, . . . . .В11, В12 (ВО);
На расстоянии [L1] от центра А и [L3] определяем положение неподвижной опоры ( точки D) . От точки D радиусом CD=90 мм чертим дугу , а от точки В радиусом ВС=90 мм чертим вторую дугу. При пересечении находим искомую точку С. Аналогично таким же методом находим 12 положений точки С: С0, С1, С2, С3, С4, С5, С6, С7, С8, С9
, С10, С11, С12 (С0).
Чтобы найти положение точки М, нужно от точки С радиусом СМ=40 мм и от точки D радиусом DM=70 мм чертим дуги. При пересечении двух дух находим положение точки М.
Затем от центра ,т.е точки А на расстоянии [L2]= 36 мм проводим вертикальный шток. При пересечении второго звена (АВ) соответственно нумеруем 12 положений точки Е : Е0, Е1, Е2, Е3, Е4, Е5, Е6, Е7, Е8, Е9, Е10, Е11, Е12 (Е0).
От каждой точки Е соответственно откладываем отрезок [EF]=60 мм и находим 12 положений точки F: F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12 (F0).
На вертикальном штоке измеряем расстояние от верхней, крайней точки до нижней ,крайней точки F (Рис.4, Чертеж 1).
F2 – F10 = Н- ход штока , F2 –нижняя , крайняя точка штока , а F10- верхняя, крайняя точка штока . F2- принимаем за начало отсчета. Из чертежа 1 измеряем расстояния,тогда
F2 F1=5мм
F2 F2=0мм
F2 F3=2мм
F2 F4=9 мм
F2 F5=12 мм
F2 F6=15мм
F2 F7=20 мм
F2 F8=28мм
F2 F9=36мм
F2 F10=40мм
F2 F11=32мм
F2 F12=19мм

Рис.1 – Траектория точек В,С,Е,F
2.1.Построение диаграммы перемещения штока
При одном полном обороте перемещение ползуна изменяется. И это изменение мы должны показать на диаграмме. Чтобы построить диаграмму нужно определить масштаб угла

Построим прямоугольную систему координат ХОУ(φОН). φ- угол поворота кривошипа; Н-ход ползуна; т.О- начало координат.
По горизонтальной оси откладываем отрезок L=120 мм, условно изображающий 360о, т.е. один полный оборот кривошипа.
Отрезок L разделим на 12 равных частей и тогда каждое деление условно изображает 30о угла поворота кривошипа.
По вертикальной оси откладываем величины: В0В1...В0В12. Полученные точки соединяем плавной кривой.
Таким образом получим диаграмму перемещения ползуна в зависимости от угла поворота кривошипа . Это кривая математически выражается Н=f(φ). (см.Рис.2)
