МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»

Архитектурно-строительный институт
Центр архитектурных, конструктивных решений и организации строительства

КОнтрольная работа
по учебному курсу «Геодезия 2»
Вариант 14

Студент	(И.О. Фамилия)
Группа
Преподаватель	(И.О. Фамилия)

Тольятти 2021
Вариант №14

1 В каких случаях применяется метод нивелирования поверхности по квадратам? Как строится сеть квадратов?

Данный метод используют при топографической съемке открытых участков местности с размеренным рельефом в больших масштабах (1:500--1:5000) с малой (0,1--0,5 м) высотой сечения рельефа с целью составления проекта вертикальной планировки и подсчета размеров земельных работ.

Последовательность работ при нивелировании по квадратам:

• 
  - рекогносцировка участка съемки;
  
• 
  - разбивка сетки квадратов и съемки ситуации;
  
• 
  - планово-высотная привязка сетки квадратов;
  
• 
  - съемка рельефа;
  
• 
  - расчетно-графические работы.
  

Рекогносцировка участка съемки. На этом этапе работ оценивают возможность без помех разбить сетку квадратов и произвести геометрическое нивелирование, выбирают начальное направление одной из сторон сетки, станции нивелирования, связующие точки, а также оптимальный вариант привязки сетки квадратов к пунктам плановой и высотной геодезической сети.

Разбивка сетки квадратов и съемка ситуации. Размеры разбиваемых на местности квадратов (от 10ґ10 м до 100ґ100 м) зависят от характера рельефа местности, заданной высоты сечения, площади участка под застройку и требований к точности изображения рельефа. Обычно начинают с разбивки внешнего полигона в виде прямоугольника или квадрата. Для этого вдоль границы снимаемого участка закрепляют опорную линию (А1-А5)

---

Теодолит устанавливали в начальную точку А1 и ориентировали по начальному направлению А1-А5. В створе этой линии через 20 м забивали колышки, т.е. закрепляли точки А2, А3 и т.д. В точках А1 и А5 при помощи теодолита откладывали прямые углы и откладывали отрезки А1- Д1 и А5-Д5. Для контроля измеряли сторону Д1-Д5, ее длина не отличалась от проектной (80 м) более чем на 1:2000. Теодолит последовательно устанавливали в точках А2, А3 и т.д. и по аналогии закрепляли внутренние вершины квадратов.

При необходимости на сторонах квадратов в точках перегиба рельефа местности закрепляют плюсовые точки. При длинах сторон внешнего полигона до 300 м разбивку заполняющих квадратов комфортно делать длинноватыми тросами, размеченными через расстояния, равные длине стороны квадрата. Одновременно с разбивкой пикетов делается съемка ситуации линейными промерами от сторон квадратов до соответствующих точек контуров и местных предметов. Результаты съемки заносят в абрис, на котором также демонстрируют стрелками направление скатов.

Вершины квадратов закрепляются колышками высотой 10 см, которые забивают так, чтобы над поверхностью земли оставалось примерно 1,5 см



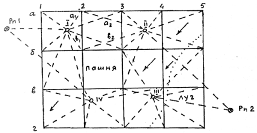
Планово-высотная привязка сетки квадратов. Для того чтобы топографический план был построен в принятой системе координат и высот, съемочное обоснование должно быть привязано к опорной геодезической сети. С этой целью сетка квадратов, являющаяся съемочным обоснованием, соединяется привязочными ходами к пунктам плановой и высотной основы.

Съемка рельефа. Перед началом нивелирования на листе плотной бумаги составляют схему квадратов, которая одновременно является и полевым журналом. Места для станций нивелирования выбирают так, чтобы с каждой из них можно было выполнить нивелирование вершин нескольких квадратов. При этом каждые две смежные станции должны иметь общие связующие точки, которые необходимы для передачи отметок на последующие станции.

Опорный ход замкнутый

В данном случае для пяти станций связующими точками выбраны вершины квадратов А2, В4, Г3, Д5 (см. рис. 1). На схеме выделяют опорный разомкнутый ход, проходящий по связующим точкам (от Rp 1 по А2, В4, Г3, Д5 до Rp 2). На рис. 1 видно, что связующие точки нивелировались дважды со смежных станций. Пунктирные линии, соединяющие станции с соответствующими вершинами квадратов, схематично изображают визирные линии при нивелировании остальных вершин квадратов. Связующие точки нивелируются с контролем по двум сторонам реек.

---

При нивелировании вершин квадратов рейку последовательно устанавливали на колышек и брали отсчеты по черной стороне рейки. Все отсчеты записывались на схеме нивелирования около соответствующей вершины.
2. Что называется горизонтом прибора? Как вычисляются отметки через превышение и горизонт прибора? Ответ дополнить схемой.

Высота визирной оси над уровнем моря или над условным уровнем называется горизонтом прибора. Как видно из рис.1, горизонт прибора, т. е. горизонт прибора равен высоте точки плюс взгляд (отсчет по рейке) на эту точку.



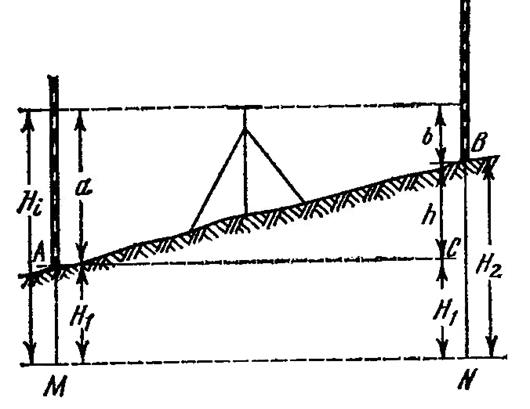
Зная горизонт прибора, легко найти высоту любой точки, на которую был сделан взгляд. Из рис.1 видно, что, т. е. высота точки равна горизонту прибора минус взгляд на эту точку.

Таким образом, по высоте какой-либо точки и по взглядам на нее и на другие точки высоты последних могут быть получены двояко: по превышениям и по горизонту прибора.

Вычислять высоты точек по горизонту прибора очень удобно, когда были сделаны взгляды на несколько точек с одной станции (точки стояния прибора) и одна из них имеет известную высоту.

При нивелировании находят разности высот (превышения) между точками; по данной высоте начальной точки и по превышениям относительно нее других точек получают высоты всех остальных точек местности. В геометрическом нивелировании превышения определяются отсчетами по вертикальным рейкам горизонтальной линией визирования нивелира. Различают нивелирование из «середины» и «вперед».

Геометрическое нивелирование из середины.

Для определения превышения точки В над точкой А (рис.1) поставим в точках А и В отвесно рейки, разделенные на сантиметры, а между ними примерно на одинаковых расстояниях - нивелир. Направив последовательно установленную горизонтально визирную ось прибора на обе рейки, делаем отсчеты по ним a и b. Из рис.1 видно, что искомое превышение h определяется из равенства.

Если считать условно точку А задней, а точку В - передней, то можно сказать, что превышение передней точки над задней равно взгляду (отсчету по рейке) назад минус взгляд (отсчет) вперед.

Если превышение по указанной формуле окажется положительным, то это покажет, что передняя точка лежит выше задней и, следовательно, линия АВ повышается. Отрицательное превышение означает, что точка В ниже точки А, т.е. линия АВ понижается.

---

Зная высоту точки А и превышение h над ней точки В, получают высоту точки В по формуле, т.е. высота последующей точки равна высоте предыдущей точки плюс соответствующее превышение.

Нивелирование вперед.

Иногда нивелир устанавливают так, что окуляр зрительной трубы приходится по отвесу над точкой А (рис.2). Вертикальное расстояние i от центра окуляра при установленной горизонтально визирной оси зрительной трубы до точки А называется высотой прибора.



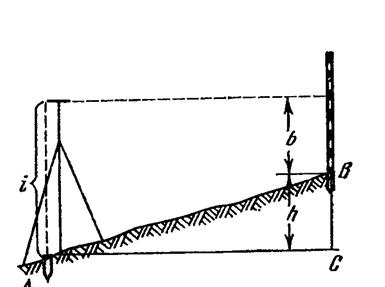
Пусть в точке В вертикально установлена рейка. Направив на нее горизонтальную визирную ось и сделав отсчет по рейке b, получим, т.е. в этом случае превышение равно высоте прибора минус взгляд вперед. Высоту прибора можно отсчитать по рейке или измерить рулеткой. Если передняя точка В выше задней А, то превышение положительно; при понижении местности от А к В превышение отрицательно.
3 Как вычисляется невязка в превышениях замкнутого нивелирного хода и разомкнутого нивелирного хода? Как вычислить допустимые невязки и как распределить поправки?

Невязки в нивелирных ходах, их допустимость и распределение

Рассмотрим разомкнутый ход нивелирования (рис.2.1). Измеренное превышение между начальной и конечной точками хода равно сумме превышений, измеренных на каждой станции, то есть

,

где   - превышение, измеренное на i-ой станции. Полученное таким образом превышение между начальной и конечной точками хода называют измеренной, или практической, суммой превышений. С другой стороны, если высота H₀ начальной точки хода и высота   конечной точки хода известны, то в соответствии с определением превышения превышение между ними может быть определено как разность их высот:

 .



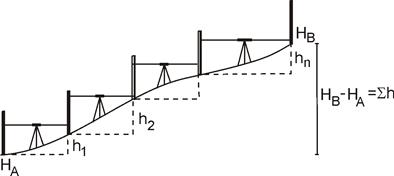
Рис. 2.1. Сумма превышений

 

Данное значение превышения между точками A и B называют теоретической суммой превышений

---

. Очевидно, что измеренная сумма превышений должна равняться теоретической

.

Но также очевидно, что вследствие ошибок измерений такое равенство будет выполняться только тогда, когда ошибки измерений полностью компенсируются. За крайне редкими исключениями такой компенсации ошибок не будет, и сумма измеренных превышений будет отличаться от теоретической суммы превышений, то есть будет иметь место соотношение

.

Разность между измеренной суммой превышений и ее теоретическим значением называется невязкой превышений

.

(В общем случае разность между результатом   измерений некоторой величины и ее теоретическим значением   называется невязкой:   . Пример: угловая невязка в треугольнике на плоскости есть разность между суммой его измеренных углов и 180°.)

В замкнутом нивелирном ходе отметка начальной точки равна отметке конечной точки, то есть H₀=H_n. Следовательно, теоретическая сумма превышений в замкнутом ходе равна

.

Тогда невязка в замкнутом нивелирном ходе будет равна измеренной сумме превышений, то есть

.

Очевидно, что величина невязки в нивелирном ходе будет зависеть от использованных приборов, тщательности выполненных измерений, внешних условий и ряда других факторов. При техническом нивелировании для оценки качества выполненных измерений превышений служит величина допустимой невязки, вычисляемая по эмпирической формуле

---

Смотрите также файлы

• В последние годы жизни Сталина Булганин вошёл в число трёхчетырёх наиболее приближённых людей.docx

• 1. Политическая власть. Ее признаки.docx

• Практическая работа Задание.docx

• Вагоны отчет по научноисследовательской работе студента Тема Исследование повреждаемости колесных пар Научный консультант.docx

• 400 лет Шории в составе России задания Найдите два термина, выпадающих.docx