Файл: КОнтрольная работа по учебному курсу Геодезия 2 Вариант 14 Студент (И. О. Фамилия).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 192
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
где L – число километров в ходе; говорят также, что L – длина хода, выраженная в километрах.
Если на каждый километр нивелирного хода приходится большое число станций (более 25), то рекомендуется использовать другую формулу:
,
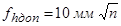где n - общее число станций в ходе.
Если полученная невязка превышений по модулю больше допустимой невязки, то есть имеет место соотношение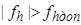
, то результаты измерений превышений не могут быть признаны удовлетворительными, и полевые измерения должны быть выполнены повторно. Если выполняется условие 
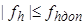, то результаты измерений считаются доброкачественными, выполненными надлежащим образом, и обработка хода может быть продолжена.
Таблица 2.1. Пример обработки журнала технического нивелирования
Но если невязка превышений допустима и не равна нулю (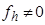
), то мы имеем определенное противоречие: измеренная сумма превышений не равна теоретической сумме превышений, чего не может быть. Поэтому полученные результаты измерения превышений нужно привести в соответствие с требованиями геометрии и здравым смыслом, “исправить” их определенным образом. В таких случаях говорят, что нужно распределить невязку, ввести в измеренные значения некоторые поправки. При этом поправки должны вводиться таким образом, чтобы сумма исправленных превышений равнялась теоретической.
Существует бесконечное число вариантов распределения поправок. При выборе такого варианта можно рассуждать следующим образом. Полевые измерения выполнялись одним и тем же прибором, по одной и той же методике, при одной и той же погоде, и прочих равных условиях, поэтому у нас нет оснований одним измерениям доверять меньше и вводить в них большие поправки, а другим измерениям доверять больше и вводить в них меньшие поправки. Представляется разумным и достаточно обоснованным считать результаты наших измерений равноточными и руководствоваться при этом принципом равенства поправок. Тогда во все измерения необходимо вводить одну и ту же поправку δ, которая может быть вычислена по формуле
,
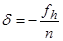где n – число станций в ходе. При этом говорят, что поправка в превышения равна невязке с противоположным знаком, деленной на число станций. Значения поправок округляются до 1 мм.
После вычисления поправок в превышения выполняется их контроль, который сводится к проверке выполнения соотношения
,
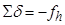то есть сумма поправок в превышения должна равняться невязке, взятой с противоположным знаком.
Так как при обработке результатов технического нивелирования значения превышений и поправки в превышения округляются до 1 мм, может случиться так, что вследствие ошибок округления последнее соотношение не выполняется, тогда некоторые поправки увеличивают или уменьшают на 1 мм так, чтобы выполнялось равенство
. Желательно, чтобы превышения с такими поправками располагались примерно равномерно по всему ходу нивелирования.
Таким образом, можно считать, что в отдельном ходе поправки вводятся поровну во все измеренные превышения с округлением до 1 мм.
Исходные данные для вычисления отметок вершин квадратов и построения топографического плана:
где l – отсчет по рейке.
6320 мм > 6317 мм
Разность составляет 3 мм. Допустимое расхождение составляет 5 мм.
6066 мм = 6066 мм
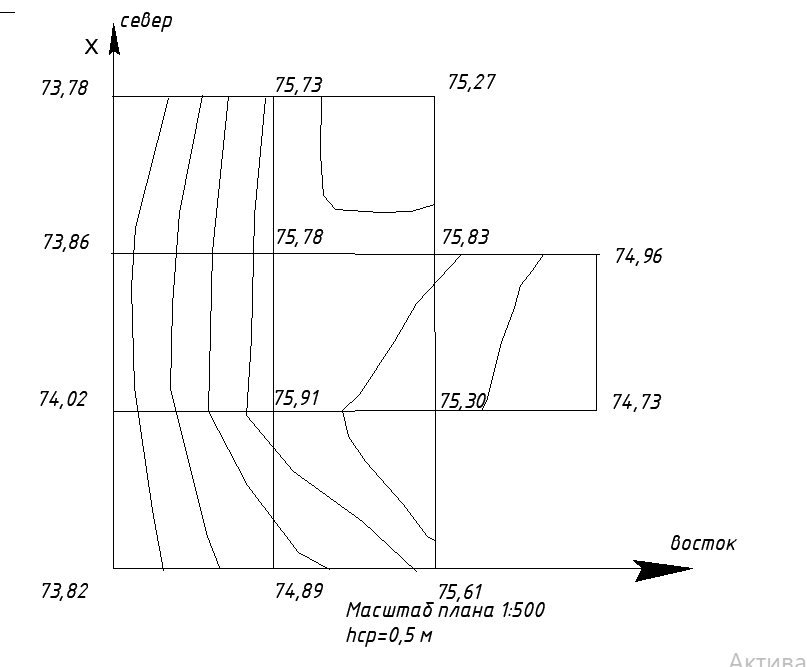
Рис. 1.3. Топографический план строительной площадки.
где Нmin – наименьшая из фактических отметок вершин квадратов, n – число квадратов.
Согласно топографическому плану (рис. 1.3.) вычисляют: h1, h2, h3, h4
где L – число километров в ходе; говорят также, что L – длина хода, выраженная в километрах.
Если на каждый километр нивелирного хода приходится большое число станций (более 25), то рекомендуется использовать другую формулу:
,где n - общее число станций в ходе.
Если полученная невязка превышений по модулю больше допустимой невязки, то есть имеет место соотношение
, то результаты измерений превышений не могут быть признаны удовлетворительными, и полевые измерения должны быть выполнены повторно. Если выполняется условие , то результаты измерений считаются доброкачественными, выполненными надлежащим образом, и обработка хода может быть продолжена.Таблица 2.1. Пример обработки журнала технического нивелирования
| № станции | № пикетов | Отсчеты по рейкам | Превышения | Горизонт прибора | Отметки | | | | | |
| Задняя | Перед. | Промеж. | Черн. | Красн. | Средн. | Испр. | | | | |
| | | | | | | | | | | |
| | | | | | | | -3 | | | |
| | Рп. 1 | | | | +1208 | +1210 | +1209 | +1206 | | 123.456 |
| | | | | | | | | | | |
| | Х1 | | | | | | | | | |
| | | | | | | | -3 | | | |
| | Х1 | | | | +1596 | +1595 | +1596 | +1593 | | 124.662 |
| | | | | | | | | | | |
| | ПК0 | | | | | | | | | |
| | | | | | | | -3 | | | |
| | ПК0 | | | | -0534 | -0537 | -0536 | -0539 | | 126.255 |
| | | | | | | | | | | |
| | ПК1 | | | | | | | | | |
| | | | | | | | -3 | | | |
| | ПК1 | | | | -0089 | -0088 | -0088 | -0091 | 126.716 | 125.716 |
| | | | | | | | | | | |
| | ПК2 | | | | | | | | | |
| | | | | | | | | | | |
| | +25 | | | | | | | | | 124.928 |
| | +41 | | | | | | -3 | | | 125.993 |
| | ПК2 | | | | -1134 | -1136 | -1135 | -1138 | | 125.625 |
| | | | | | | | | | | |
| | ПК3 | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | -3 | | | |
| | ПК3 | | | | +2294 | +2296 | +2295 | +2292 | | 124.487 |
| | | | | | | | | | | |
| | Рп.2 | | | | | | | | | 126.779 |
| | | | | | | | | | | |
| | | | | | | | | | | |
| | S | | | | |  | +3341 | +3323 | | |
 | +3340 | | |    | +3323 +18  | =30 мм | | | | |
Но если невязка превышений допустима и не равна нулю (
), то мы имеем определенное противоречие: измеренная сумма превышений не равна теоретической сумме превышений, чего не может быть. Поэтому полученные результаты измерения превышений нужно привести в соответствие с требованиями геометрии и здравым смыслом, “исправить” их определенным образом. В таких случаях говорят, что нужно распределить невязку, ввести в измеренные значения некоторые поправки. При этом поправки должны вводиться таким образом, чтобы сумма исправленных превышений равнялась теоретической.Существует бесконечное число вариантов распределения поправок. При выборе такого варианта можно рассуждать следующим образом. Полевые измерения выполнялись одним и тем же прибором, по одной и той же методике, при одной и той же погоде, и прочих равных условиях, поэтому у нас нет оснований одним измерениям доверять меньше и вводить в них большие поправки, а другим измерениям доверять больше и вводить в них меньшие поправки. Представляется разумным и достаточно обоснованным считать результаты наших измерений равноточными и руководствоваться при этом принципом равенства поправок. Тогда во все измерения необходимо вводить одну и ту же поправку δ, которая может быть вычислена по формуле
,где n – число станций в ходе. При этом говорят, что поправка в превышения равна невязке с противоположным знаком, деленной на число станций. Значения поправок округляются до 1 мм.
После вычисления поправок в превышения выполняется их контроль, который сводится к проверке выполнения соотношения
,то есть сумма поправок в превышения должна равняться невязке, взятой с противоположным знаком.
Так как при обработке результатов технического нивелирования значения превышений и поправки в превышения округляются до 1 мм, может случиться так, что вследствие ошибок округления последнее соотношение не выполняется, тогда некоторые поправки увеличивают или уменьшают на 1 мм так, чтобы выполнялось равенство
. Желательно, чтобы превышения с такими поправками располагались примерно равномерно по всему ходу нивелирования.Таким образом, можно считать, что в отдельном ходе поправки вводятся поровну во все измеренные превышения с округлением до 1 мм.
Исходные данные для вычисления отметок вершин квадратов и построения топографического плана:
-
М 1:500 -
l = 20 м -
hср = 0,25 м -
-
-
-
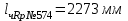
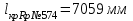
α0 = 120º00' -
i0 = 0,025
-
Вычисление горизонта прибора на I станции
-
Вычисляют горизонт прибора на I станции, используя отметку репера №574 и отсчеты по красной и черной сторонам рейки, установленной на репере
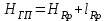 , | (1.1) |
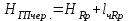 , | (1.2) |
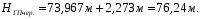 , | (1.3) |
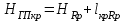 , | (1.4) |
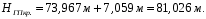 . | (1.5) |
-
Вычисление отметок всех вершин квадратов пронивелированных с I станции
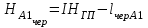 , | (1.6) |
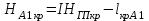 , | (1.7) |
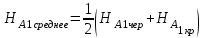 . | (1.8) |
| НА1чер= 76,24– 2,421 м = | 73,819 | м | НА1ср= | 73,820 | м |
| НА1кр= 81,026– 7,205 м = | 73,821 | м | |||
| НБ1чер= 76,24– 1,355 м = | 74,885 | м | НБ1ср= | 74,885 | м |
| НБ1кр= 81,026– 6,142 м = | 74,884 | м | |||
| НА2чер= 76,24– 2,225 м = | 74,015 | м | НА2ср= | 74,016 | м |
| НА2кр= 81,026– 7,010 м = | 74,016 | м | |||
| НБ2чер= 76,24– 0,334 м = | 75,906 | м | НБ2ср= | 75,906 | м |
| НБ2кр=81,026– 5,120 м = | 75,906 | м | |||
| НА3чер= 76,24– 2,379 м = | 73,861 | м | НА3ср= | 73,862 | м |
| НА3кр= 81,026– 7,164 м = | 73,862 | м | |||
| НБ3чер= 76,24– 0,461 м = | 75,779 | м | НБ3ср= | 75,780 | м |
| НБ3кр= 81,026– 5,245 м = | 75,781 | м | |||
| НА4чер= 76,24– 2,466 м = | 73,774 | м | НА4ср= | 73,775 | м |
| НА4кр= 81,026– 7,251 м = | 73,775 | м | |||
| НБ4чер= 76,24– 0,516 м = | 75,724 | м | НБ4ср= | 75,725 | м |
| НБ4кр= 81,026– 5,300 м = | 75,726 | м |
-
Выполняют контроль взятия отсчетов на связующих точках Б2 и Б3 пронивелированых с двух станций:
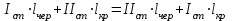 , | (1.9) |
где l – отсчет по рейке.
-
Вершина квадрата Б3: 0461 мм + 5859 мм >1072 мм + 5245 мм
6320 мм > 6317 мм
Разность составляет 3 мм. Допустимое расхождение составляет 5 мм.
-
Вершина квадрата точка Б2: 0334 мм + 5732 мм = 0946 мм + 5120 мм
6066 мм = 6066 мм
-
Вывод: контроль удовлетворяет требованиям, значит вершины квадратов: Б2 и Б3 можно использовать для вычисления горизонта прибора на II станции.
-
Вычисление горизонта прибора на II станции
-
Вычисляют горизонт прибора на II станции, используя вычисленные отметки связующих точек (вершин) Б2, Б3 и результаты нивелирования этих вершин на II станции: -
вершина Б3: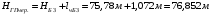
,
(1.10)
.
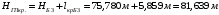(1.11)
-
вершина Б2: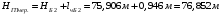
,
(1.12)
.
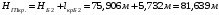(1.13)
-
Вывод: средние значения ГП, полученные по результатам нивелирования вершин Б2 и Б3 принимают за окончательные и используют для вычисления отметок вершин квадратов, пронивелированных на станции II.
-
Вычисление отметок всех вершин квадратов пронивелированных с II станции
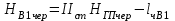 , | (1.14) | |||||
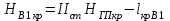 , | (1.15) | |||||
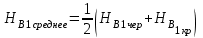 . | (1.16) | |||||
| НВ1чер= 76,852м– 1,092 м = | 75,760 | м | НВ1ср= | 75,761 | м | |
| НВ1кр= 81,639м– 5,878 м = | 75,761 | м | ||||
| НВ2чер= 76,852м– 1,553 м = | 75,299 | м | НВ2ср= | 75,300 | м | |
| НВ2кр=81,639м – 6,338 м = | 75,301 | м | ||||
| НВ3чер= 76,852м– 1,021 м = | 75,831 | м | НВ3ср= | 75,832 | м | |
| НВ3кр= 81,639м– 5,807 м = | 75,832 | м | ||||
| НВ4чер= 76,852м– 1,583 м = | 75,269 | м | НВ4ср= | 75,270 | м | |
| НВ4кр= 81,639м– 6,368 м = | 75,271 | м | ||||
| НГ2чер= 76,852м– 2,127 м = | 74,725 | м | НГ2ср= | 74,726 | м | |
| НГ2кр= 81,639м– 6,912 м = | 74,727 | м | ||||
| НГ3чер= 68,991 м – 1,896 м = | 74,956 | м | НГ3ср= | 74,956 | м | |
| НГ3кр=81,639м– 6,683 м = | 74,956 | м | ||||
-
Построение топографического плана по результатам нивелирования строительной площадки
-
Для построения топографического плана по результатам нивелирования поверхности строительной площадки вычерчивают сеть квадратов в масштабе М 1:500. Сторону А1–А4 ориентируют на север и принимают за ось абсцисс – Х, а сторону А1–В1 принимают за ось ординат – Y. -
В каждой вершине квадрата подписывают вычисленные отметки с точностью до 0,01 м. По всем сторонам квадратов и по диагоналям (направлениям скатов местности) выполняют интерполирование горизонталей.
Рис. 1.3. Топографический план строительной площадки.
-
Вычисление проектной отметки горизонтальной площадки.
-
Вычисляют проектную отметку горизонтальной площадки по формуле:
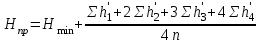 , | (2.1) |
где Нmin – наименьшая из фактических отметок вершин квадратов, n – число квадратов.
-
Для облегчения расчетов вводят в расчетную формулу понятие: условная отметка h. Вычисляют условную отметку для каждой вершины квадрата:
| h = Hфакт – Нmin. | (2.2) |
Согласно топографическому плану (рис. 1.3.) вычисляют: h1, h2, h3, h4
-
h1 – сумма отметок вершин квадратов, принадлежащих только одному квадрату;
h1 = HА1 + НА4 + НВ4 + НГ3 + НГ2 + НВ1.
(2.3)
-
h2 – сумма отметок вершин квадратов общих для двух смежных квадратов:
h2 = НБ4 + НБ1 + НА2 + НА3.
(2.4)
-
Полученную сумму h2 подставляют в формулу (2.1): -
h3 – сумма отметок вершин квадратов общих для трех смежных квадратов: