ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4.1 Тісті беріліс механизмінің схемасын сипаттау.
4.1-суретте планетарлық сатысы бар беріліс механизмінің диаграммасы көрсетілген. Механизм жылжымалы звенодан Н (тасымалдаушы), Z2 спутниктер блогынан, Z3 тірек доңғалағынан, Z1 тісті доңғалағынан тұрады.
| Параметр аты | Белгіленуі | Бірлік | Құндылықтар |
| Иінді біліктің бұрыштық жылдамдығы (1 беріліс) | ω1 | s-1 | 840 |
| Беріліс қатынасы | 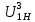 | - | 3.1 |
| Беріліс модулі | м | мм | 2.0 |
| Спутниктердің саны | TO | - | 3 |
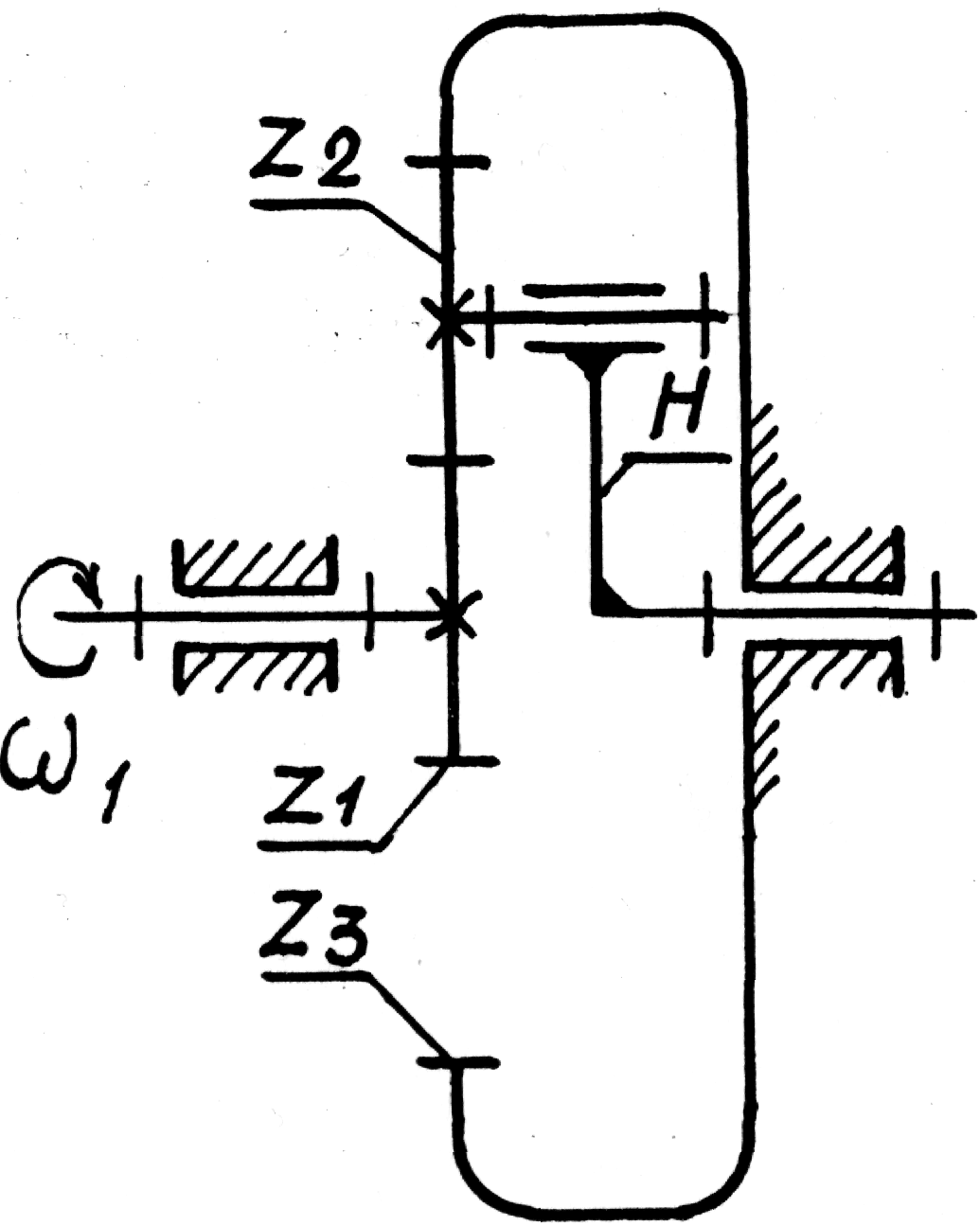
4.1-сурет – Планетарлық сатысы бар беріліс механизмінің схемасы
4.2 Планетарлық берілістің тіс санын таңдау.
Планетарлық беріліс қорабының тістерінің санын таңдау келесі реттілікпен жүзеге асырылады.
Планетарлық беріліс сатысының беріліс қатынасының формуласын жазамыз:
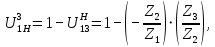
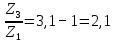
Осы планетарлық беріліс үшін туралау шартын жазайық:
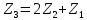
Z3, Z2 дөңгелегі тістерінің санын анықтайық:
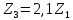
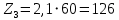
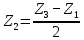
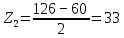
Планетарлық беріліс қорабының тістерінің санын таңдағаннан кейін біз мына схеманы тексереміз:
-
берілген беріліс коэффициенті (рұқсат етілген дәлдікпен); -
теңестіру шарты; -
көршілестік жағдайы (бірнеше спутниктерді орналастыру); -
құрастыру шарты (спутниктер арасындағы бұрыштардың тең болуы шарты); -
дұрыс араласу шарты.
1. Берілген беріліс қатынасы:
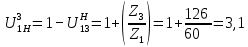
Беріліс қорабының есептелген беріліс коэффициенті көрсетілгенге тең.
2. Туралау шарты:
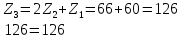
Шарт орындалды.
3. Көршінің жағдайы:
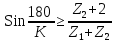
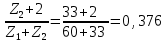
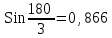
0,866>0,376
Көршілестік шарты орындалды.
4. Құрастыру шарты:
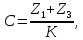
мұндағы K – жерсеріктердің саны;
C – бүтін сан.
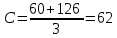
Шарт орындалды.
5. Дұрыс қосылу шарты:
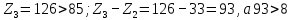
Шарт орындалды.
4.3 Беріліс қорабының схемасын құру
Біз беріліс қорабының барлық тісті доңғалақтарының қадам шеңберлерінің радиустарын анықтаймыз:
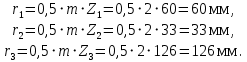
Тісті беріліс тізбегінің масштаб коэффициентін таңдау
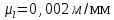
Содан кейін дөңгелектердің масштабының радиустары дөңгелектердің нақты радиустарын редуктор схемасының масштабтық коэффициентіне бөлудің коэффициенті ретінде анықталады.
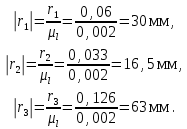
Берілген масштабта беріліс қорабының кинематикалық диаграммасын саламыз.
4.4 Жылдамдықтардың суретін және жоспарын құру
беріліс қорабының бұрыштық жылдамдықтары.
Жылдамдықтардың суретін салу үшін біз ордината сызығын саламыз және оған беріліс қорабының барлық сипаттамалық нүктелерін проекциялаймыз.
1 және 2 дөңгелектерге жататын А нүктесінің жылдамдығын анықтаңыз
(біріктірілген нүкте):
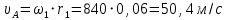
Жылдамдық үлгісінің масштабтық коэффициентін анықтаймыз:
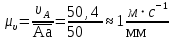
А нүктесінен 1-дөңгелектің А нүктесінің жылдамдық векторын бейнелейтін Aa = 50 мм кесіндісін шетке шығарамыз. А нүктесін О нүктесімен (О нүктесінің жылдамдығы нөлге тең) қоса отырып, 1 түзуін аламыз, ол 1-дөңгелектің жылдамдықтарының таралу сызығы.
2-дөңгелекке көшейік.Бұл дөңгелекте А нүктесінің жылдамдығы (ол 1-дөңгелектің А нүктесінің жылдамдығымен бірдей) және С нүктесінің жылдамдығы (оның жылдамдығы нөлге тең). Демек, а және С нүктелерін қоса отырып, 2-ші дөңгелектің жылдамдықтарының таралу сызығы болып табылатын 2 түзуін аламыз.
H тасымалдаушысына өтеміз. В нүктесінен жылдамдықтардың таралу сызығымен қиылысқанша көлденең түзу жүргіземіз 2. Біз b нүктесін аламыз - спутник осінің жылдамдығы сегментінің соңы 2. Сол кезде уақыт, бұл H тасымалдаушы осінің жылдамдығы. b және O нүктелерін қосу; (О нүктесінің жылдамдығы нөлге тең – тасымалдаушының айналу осі), Н түзу сызығын аламыз, ол H тасымалдаушысының жылдамдықтарының таралу сызығы болып табылады.
Бұрыштық жылдамдықтардың жоспарын құру үшін масштаб коэффициентін анықтаймыз:
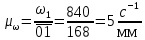
Біз түзуге перпендикуляр түзу жүргіземіз және оған 01 = 168 мм кесіндіні шетке қоямыз. 1 нүктеден жылдамдық үлгісінің 1 сызығына параллель сәулені ОП тік сызығымен қиылысқанша жүргіземіз. Р нүктесінен – бұрыштық жылдамдық жоспарының полюсі 2, 3 және H түзулеріне параллель сәулелерді саламыз. Алынған 0-1, 0-2, 0-3 және O-H кесінділері сәйкес бұрыштық жылдамдықтарға пропорционал:
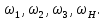
Бұрыштық жылдамдық жоспарын пайдалана отырып, беріліс қорабының беріліс қатынасын графикалық түрде анықтауға болады:
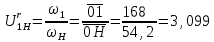
Есептердегі сәйкессіздіктің пайызын анықтаңыз:
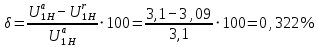
Рұқсат етілген қате 6-8% құрайтын инженерлік есептеулердің дәлдігінен аспауы керек.
4.5 Эвольвентті буынның суретін салу.
Эвольвентті тарту үлгісінің масштабтық коэффициентін таңдау
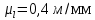немесе ГОСТ бойынша 4:1.Біз беріліс қорабының барлық тісті доңғалақтарының қадам шеңберлерінің радиустарын анықтаймыз:
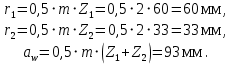
Қалыпты дөңгелектерде қадам шеңбері бастапқымен сәйкес келеді.
Орталық қашықтықты қалдырыңыз
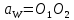
ал О1 және О2 дөңгелектерінің центрлерінен радиустары r1 және r2 болатын бөлу шеңберлерін саламыз.
Бөлгіш шеңберлердің жанамасының Р нүктесін түйісу полюсі деп атайды.
Жалғау полюсі P арқылы біз ортақ жанама T - T және қосылу бұрышында жүргіземіз
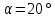- N - N келісім сызығы (генерациялау желісі). T - T жанама O1 - O2 центрлерінің сызығына қатаң перпендикуляр салынуы керек.Z1 және Z2 берілістерінің негізгі шеңберлерінің радиустарын формулалар бойынша анықтаймыз:
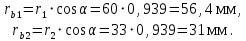
Біз радиустары бар негізгі шеңберлерді саламыз
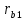және
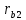.Тексеріңіз: бұл шеңберлер N - N сызығына тиіп тұруы керек (бірақ қиылыспауы керек). O1 және O2 дөңгелектерінің центрлерінен O1A және O2B перпендикулярларын N - N қосылу сызығына түсіреміз. Біз A және B нүктелерін аламыз. Шарт сызығының АВ кесіндісі теориялық байланыс сызығы деп аталады.
А және В нүктелерінің орнын дәлірек анықтау үшін формулаларды қолданамыз:
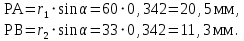
Z1 және Z2 берілістерінің шыңдарының шеңберлерінің радиустарын формулалар бойынша анықтаймыз:
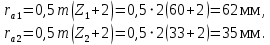
Біз радиустары бар негізгі шеңберлерді саламыз
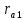және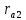
.Радиус төбелерінің шеңбер қиылысы
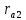N - N түйісу сызығымен а нүктесін береді, ал радиус төбелерінің шеңберінің қиылысуы 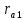N–N қосылу сызығымен b нүктесін береді.N - N келісім сызығының ab сегменті әрекеттесудің белсенді сызығы деп аталады. ω1 және ω2 берілістерінің көрсетілген айналу бағытымен жұп тістердің қосылуы а нүктесінен басталып, b нүктесінде аяқталады.
Z1 және Z2 берілістерінің шыңдарының шеңберлерінің радиустарын формулалар бойынша анықтаймыз:
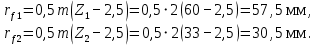
Көрсетілген радиустары бар ойпат шеңберлерін саламыз.
Тіс профильдері инволюталар арқылы сызылған. Эвольвентті салу үшін түзу сызықты шығаратын және оған нүкте салатын негізгі шеңбер болуы керек. Әдетте, сызба нүктесі ретінде Р звеносының полюсі алынады.
N - N генерациялау сызығын бірінші негізгі шеңбер бойымен (радиусы
) бірінші дөңгелектің эвольвенті (тіс профилі) шығады. N - N генерациялау сызығын екінші негізгі шеңбер бойымен (радиусы
) екінші дөңгелектің эвольвенті (тіс профилі) алынады.Екінші дөңгелектің эвольвентін (тіс профилін) тұрғызу үшін RV сегментін тең бөліктерге бөлеміз, мысалы, төртке. Әрбір бөліктің ұзындығы h болсын. Негізгі шеңбер доғасының бойымен В нүктесінен кішкене сегменттерді бір жаққа қойыңыз
оң және сол. 1,2,3,4,…,7 бөлу нүктелерін белгілейік.1,2,3,4,…,7 нүктелері доңғалақтың центрімен О2 радиустары арқылы байланысқан және алынған 1,2,3,4,…,7 нүктелерінің әрқайсысында радиустың негізгі шеңберіне жанамаларды саламыз.
. 1-ші нүктеден тангенциалды түрде бір кішкене h кесіндісін, 2-ші нүктеден - 2h және т.б. Алынған нүктелерді тегіс қисық сызықпен байланыстырамыз, негізгі шеңберден шыңдар шеңберіне дейін салынған эволюцияны аламыз.Тістің эвольвентті емес бөлігі (радиустың негізгі шеңберінен
радиустың ойыстарының шеңберіне дейін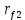 
) алдымен радиус бойымен сызылады, радиус бойынша дөңгелектеу орындалады.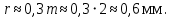
Біз тістің қалыңдығын формула бойынша қадамдық шеңберлер бойынша анықтаймыз:
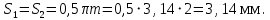
r2 бөлетін шеңбер бойымен P түйісу полюсынан S2/2 тісінің қалыңдығының жартысына тең қашықтықты бөліп алып, тістің симметрия осін табайық. Біз симметрия осін сызамыз және осы оське қатысты біз сызылғанға симметриялы дұрыс тіс саламыз.
Бөлу шеңберінің бойымен айналмалы қадамның өлшемін есептейміз
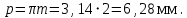
және Z2 дөңгелектің бұрыштық қадамы формула бойынша:
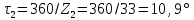
Екінші тісті тұрғызу үшін бірінші тістің симметрия осінен бұрыштық қадамның мәнін кейінге қалдырамыз.
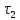бұрыштың жанамасының мәні бойынша. Екінші тістің симметрия осін аламыз. Симметрия осіне ие болғандықтан, екінші тісте салу қиын емес.