Файл: Определение длины световой волны при помощи бипризмы френеля (Лабораторная работа 64).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 238
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ПРИ ПОМОЩИ БИПРИЗМЫ ФРЕНЕЛЯ (Лабораторная работа 64)
ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТА
ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ С ПОМОЩЬЮ ЛАЗЕРА (Лабораторная работа 78)
ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТА
ПОЛУЧЕНИЕ И ИССЛЕДОВАНИЕ ПОЛЯРИЗОВАННОГО СВЕТА (Лабораторная работа 69)
ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТА
ИЗУЧЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ (Лабораторная работа 80)
ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТА
ИЗУЧЕНИЕ ЗАКОНОВ ФОТОЭФФЕКТА (Лабораторная работа 81)
ПРОТОКОЛ ИЗМЕРЕНИЙ
Результаты измерений
| Светофильтр | мм | мм | | мм | мм | мм | мм | мм | мм |
| Красный | | | | | | | | | |
Расчеты
Ширина интерференционной картины:
Расстояние между двумя темными полосами:
Расстояние между изображениями мнимых источников:
Истинное расстояние между мнимыми источниками:
Длина волны:
Выводы
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
ВОПРОСЫ ДЛЯ ДОПУСКА
-
Какие волны называются когерентными?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Как записывается выражение для амплитуды результирующих колебаний?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Какие источники называются когерентными?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Почему свет от естественных источников не является когерентным?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Как создать когерентные источники?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
В чем заключается явление интерференции?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Как связана оптическая разность хода с разностью фаз?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
-
Как записываются условия максимума и минимума интерференции для разности хода? Для разности фаз?
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
_______________________________________________________________________________________________________
Примечание: При затруднениях с ответами на вопросы используйте /2, § 1.3 – 1.4/
ТЕСТ
-
Какая из приведённых пар волн является когерентной?
а)
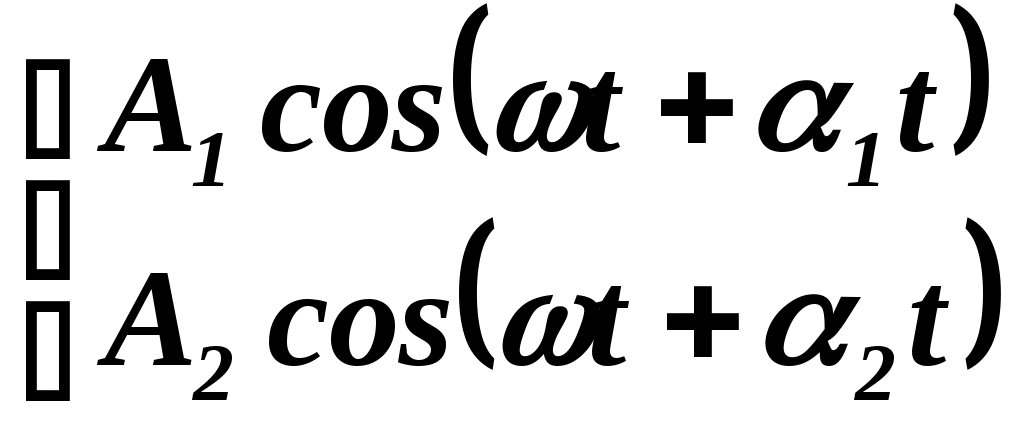 ; б)
; б) 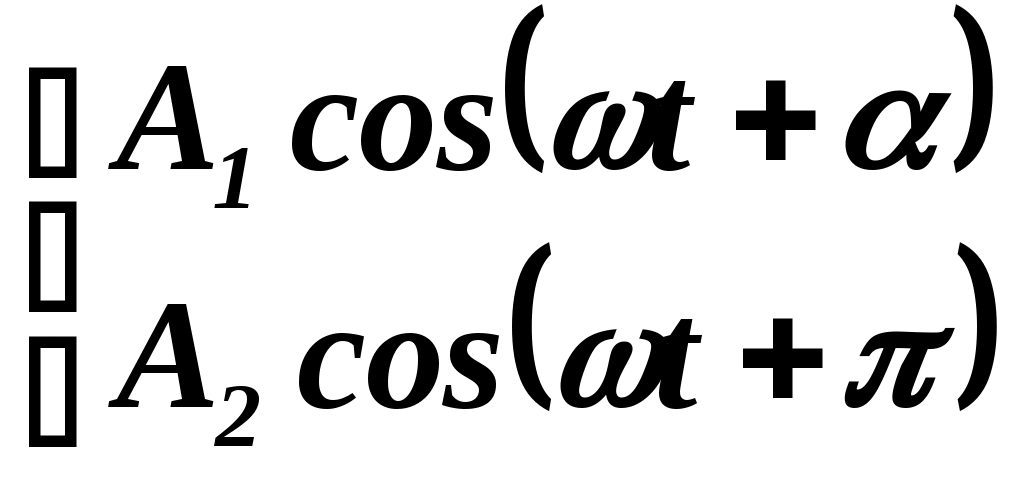 ; в)
; в)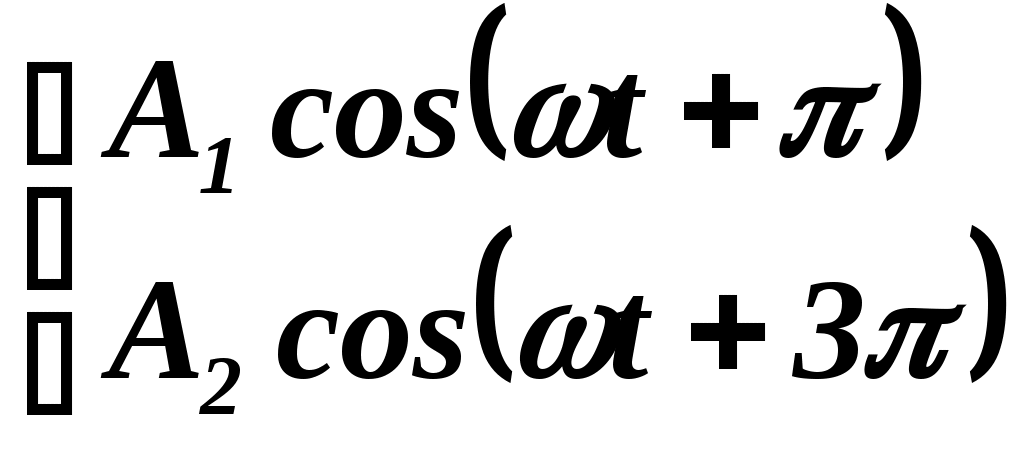 .
.-
Чему равна интенсивность (I) света, полученного при сложении когерентных волн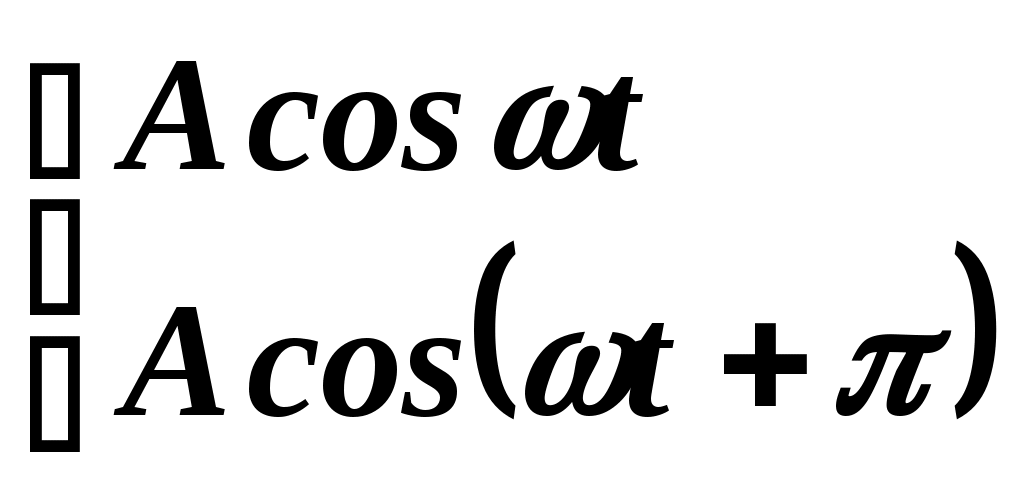 ?
?
а)
-
Чему равна интенсивность (I) света, полученного при сложении когерентных волн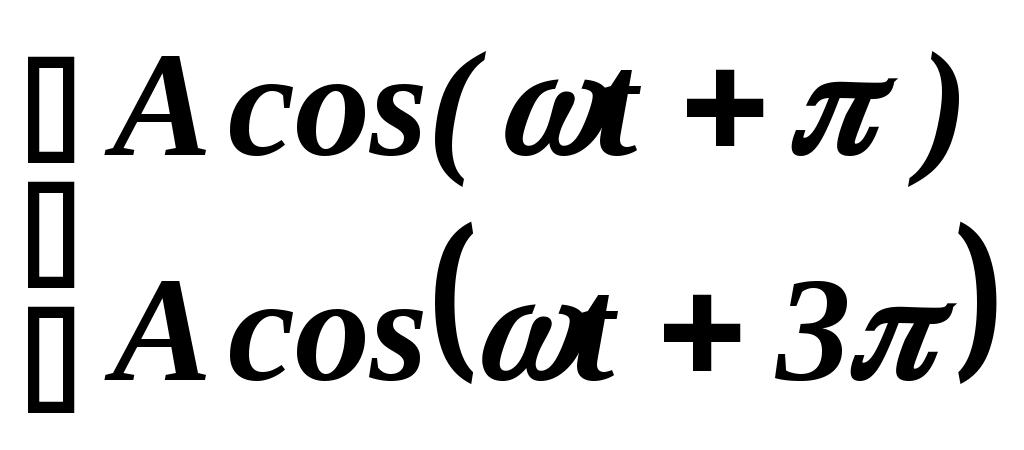 ?
?
а)
-
Какие из перечисленных источников являются когерентными?
а) Две раскаленные линии.
б) Лазерный луч.
в) Солнечные лучи, прошедшие через призму.
г) Лучи, полученные при прохождении через бипризму Френеля.
-
Как зависит ширина интерференционной зоны от преломляющего угла бипризмы?
а) Чем больше угол
б) Чем меньше угол
в) Ширина зон интерференции не зависит от величины угла
ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ С ПОМОЩЬЮ ЛАЗЕРА
(Лабораторная работа 78)
Цель работы: изучить явление дифракции света.
Явление дифракции света заключается в отклонении световых волн от прямолинейного пути при огибании светом малых препятствий в оптически однородной среде.
Дифракция характерна для волнового процесса. Выделяют два случая дифракции: дифракцию сферических световых волн (дифракцию Френеля), которая наблюдается при конечном расстоянии преграды от экрана; дифракцию в параллельных лучах (дифракцию Фраунгофера) для плоских световых волн. Во втором случае дифракция наблюдается только с помощью линзы, собирающей лучи в фокальной плоскости, или глазом, аккомодированным на бесконечность.
В
 основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны.
основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны. Принцип Гюйгенса-Френеля рассматривает интенсивность результирующей волны как результат интерференции вторичных волн.
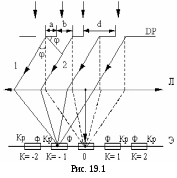
Рассмотрим дифракцию света при прохождении через дифракционную решетку (рис. 19.1).
Простейшая дифракционная решётка представляет собой стеклянную пластинку, на которую нанесены параллельные друг другу царапины, а между ними оставлены узкие неповрежденные полоски, то есть дифракционная решетка – это система одинаковых щелей.
Сумма размеров прозрачной (
Свет, проходя через узкие щели решетки, испытывает дифракцию, то есть отклоняется от первоначального направления. Дифрагирующие лучи от отдельных щелей налагаются друг на друга в фокальной плоскости линзы и интерферируют между собой. Если число щелей равно
Пусть свет с длиной волны
I и 2
Если
где
Условие (19.1) определяет положение главных максимумов.
Положение минимумов определяется условием:
где
Причем эти минимумы получаются там же, где были минимумы от одной щели.
Добавочные минимумы определяются соотношением:
где
М
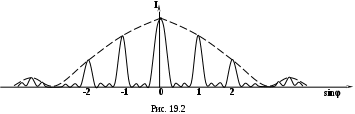
ежду двумя главными максимумами располагается