ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Содержание
1. Основные типы соединений…………………………………………………..3
2. Правила преобразования структурных схем линейных систем…………….7
3. Вычисление передаточной функции одноконтурной системы…………….10
4. Вычисление передаточной функции многоконтурной системы…………...13
Список литературы………………………………………………………………14
1. Основные типы соединений
Структурная схема – это графическое представление математической модели системы в виде соединений звеньев, условно обозначаемых в виде прямоугольника с указанием входной и выходной величин и передаточных функций. Обозначение передаточной функции записывают, как правило, внутри прямоугольника.
Суммирующие звенья изображаются в виде круга, разделенного на секторы. Сектор, на который подается величина с обратным (отрицательным) знаком, затемняют или перед соответствующим входом ставят знак минус.
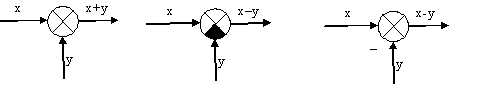
а б в
Рисунок 1 – Схемы суммирующих звеньев
Звено – это устройство любого физического вида и конструктивного оформления, но описанное определенным дифференциальным уравнением. Звено – математическая модель любой части САУ.
Математическая модель – это описание каких-либо явлений, процессов с помощью математической символики.
Математическое моделирование – изучение явлений с помощью математических моделей процессов.
При математическом описании систему обычно изображают в виде функциональной схемы. Для каждого блока составляют уравнение, которым описываются процессы. Затем строится структурная схема. Преобразования, необходимые для получения уравнений и передаточных функций системы, проще и нагляднее производить по структурным схемам. Звено структурной схемы необязательно изображает модель какого–либо элемента. Оно может быть моделью элемента, соединения элементов или вообще любой частью системы.
Основные типы соединений:
-
Последовательное соединение звеньев – это соединение, при котором выходная величина предшествующего звена является входной величиной последующего звена. -
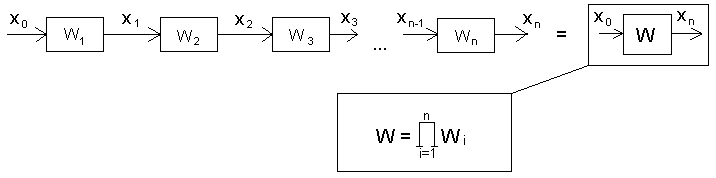
Рисунок 2 – Последовательное соединение звеньев
При преобразовании цепочку из последовательно соединенных звеньев, заменяют одним звеном с передаточной функцией равной произведению передаточных функций отдельных звеньев.
2)Параллельное соединение звеньев – это соединение, при котором на вход всех звеньев подается одно и то же воздействие, а выходные величины складываются.
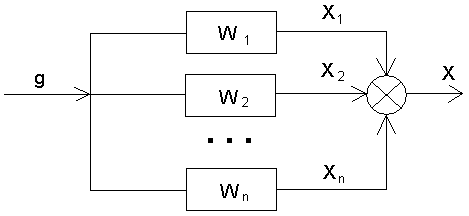
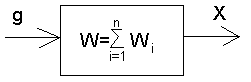
Рисунок 3 – Параллельное соединение звеньев
Цепь из параллельно соединенных звеньев можно заменить одним звеном с передаточной функцией, равной сумме передаточных функций входящих в нее звеньев.
3) Обратное соединение звеньев – это соединение, при котором звено охвачено обратной связью, а именно, выходной сигнал одного звена через какое-либо другое звено подается на вход первого.
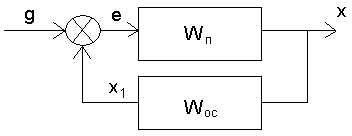
Рисунок 4 – Обратное соединение звеньев
Участок цепи от точки приложения входного воздействия g до точки съёма выходного сигнала
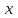(в направлении распределения сигнала) называется прямой цепью.Участок цепи от точки съема выходного сигнала
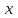до сумматора 
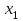называется обратной связью.
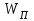– передаточная функция прямой цепи.
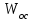- передаточная функция обратной связи (ОС).Если сигнал обратной связи
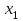вычитается из входного воздействия 
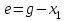, то обратная связь называется отрицательной обратной связью.Если сигнал обратной связи
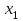складывается со входным воздействием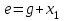 
, то обратная связь называется положительной обратной связью.
Если передаточная функция обратной связи
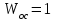, то обратная связь называется единичной, и структурную схему изображают так, как показано на рис. 5.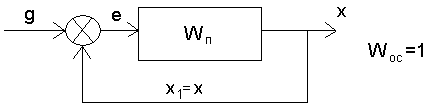 
Рисунок 5 – Обратное соединение звеньев с единичной отрицательной обратной связью
При размыкании замкнутой цепи сразу после сумматора получается цепь из 2-х последовательно соединенных звеньев.
Ее передаточная функция, равная
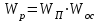называется передаточной функцией разомкнутой цепи (системы).Передаточная функция звена, охваченного обратной связью, равна передаточной функции
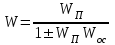, где плюс в знаменателе правой части берется при отрицательной обратной связи, минус – при положительной.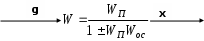
2. Правила преобразования структурных схем линейных систем
При преобразовании структурных схем возникает необходимость переноса сумматоров и узлов схем.
1. Перенос сумматора.
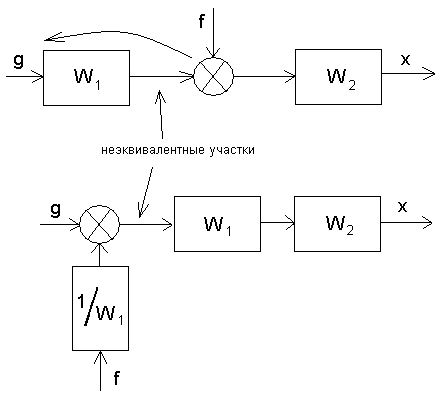
1.1. При переносе сумматора по ходу сигнала добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор.
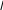
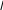
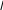
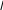
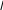
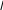
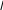
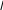
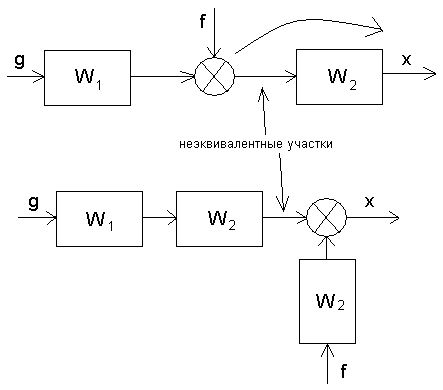
1.2. При переносе сумматора против хода сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор.
1.3. При переносе сумматора возникают неэквивалентные участки цепи, поэтому нельзя переносить сумматор через точку съема сигнала.
2. Перенос узла.
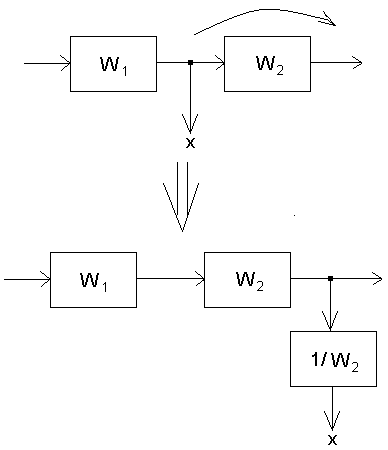
2.1. При переносе узла по ходу сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел.
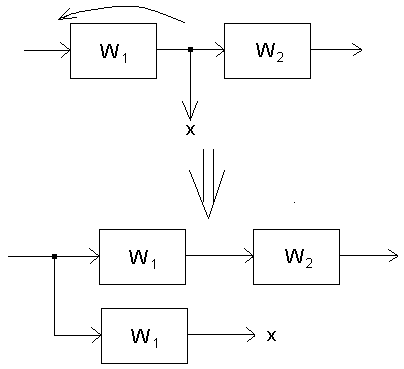
2.2. При переносе узла против хода сигнала добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел.
3. Перестановка узлов. Узлы можно переставлять местами
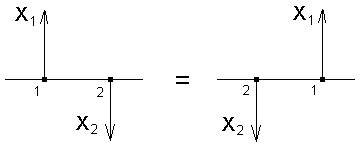
4.Перестановка сумматоров. Сумматоры можно менять местами, но при этом участки между сумматорами не являются эквивалентными.
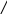
5. При переносе узла через сумматор добавляется сравнивающее звено.
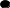
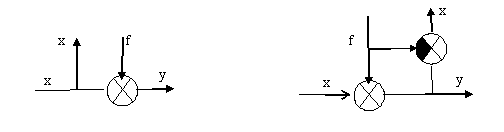
6. При переносе сумматора через узел добавляется суммирующее звено.
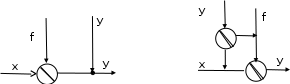
3. Вычисление передаточной функции одноконтурной системы
Замкнутая система называется одноконтурной, если при ее размыкании (сразу после сумматора) получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных соединений и обратных связей.
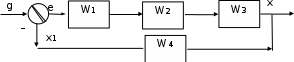
Рисунок 6 – Пример одноконтурной системы
Прямая цепь – участок по ходу сигнала от точки приложения входного воздействия до точки съема выходного сигнала.
Разомкнутая цепь – цепь из последовательно соединенных звеньев, входящих в замкнутый контур.
Для одноконтурной системы справедливо правило:
Передаточная функция одноконтурной системы с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи деленной на единицу плюс (минус) передаточная функция разомкнутой системы.
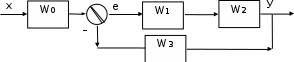
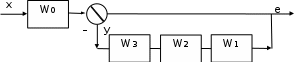
Пример: Определить передаточную функцию системы по входу
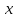и выходу 
– 
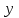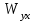; по входу 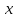и выходу 
– 
.
;
; 
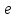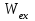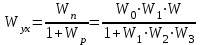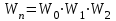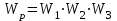
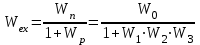
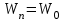
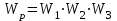
4. Вычисление передаточной функции многоконтурной системы
Замкнутая система называется многоконтурной если при ее размыкании получается цепь, содержащая параллельные и обратные связи, или иначе если она кроме главной обратной вязи содержит параллельные или местные обратные связи.
Многоконтурная система имеет перекрещивающиеся связи, если контур обратной или параллельной связи охватывает участок цепи, содержащий только начало или конец другой цепи обратной или параллельной связи.
