Файл: Задача Методом изоклин построить интегральные уравнения.docx
Добавлен: 10.01.2024
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
МАТЕМАТИКА
Группа Ср22ГУ171в
Студент
Белоусова Д.А.
МОСКВА 2023
Ответы на задания по практической работе.
Задача 1.
Методом изоклин построить интегральные уравнения.
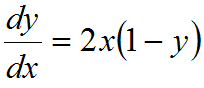
Если принять y’=k, то уравнение изоклины для заданного уравнения: k=2x(1-y) или
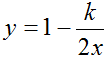уравнение гипербол. Для примера ограничимся значениями: k1=1 k2=1 k3=10 Чертеж с интегральными кривыми:
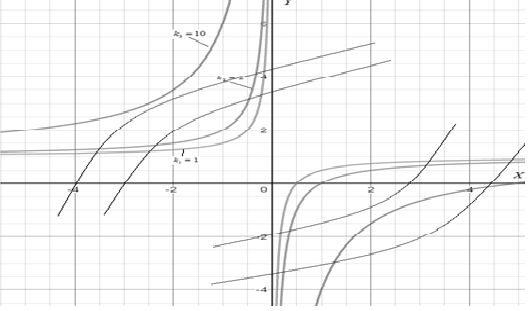
Задача 2.
Решить уравнения, допускающие понижение порядка
x^2 y^''=y^'2.Замена y^'=z(x),y^''=z'
x^2 z^'=z^2
Поделим на z≠0. Если z=0,то y=C-решение
Поделим на x≠0.x=0-не решение.
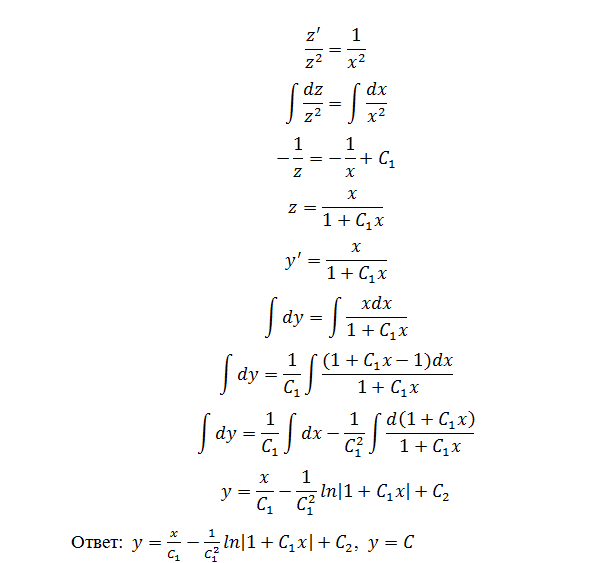
Задача № 3
Решить систему уравнений
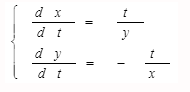
Решение:
Решаем методом подстановки:
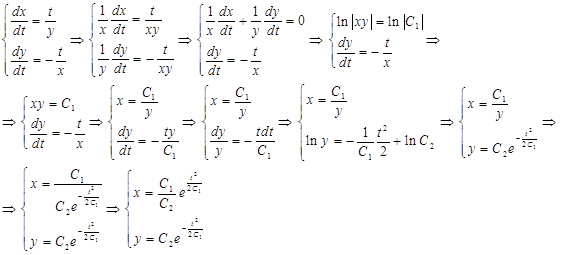
Ответ:
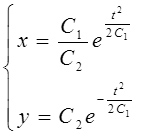
Задача 4.
Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?
Решение
Если производится n независимых испытаний, при каждом из которых вероятность осуществления события A постоянна и равна p. а вероятность противоположного события равна q=1-p, то число успехов м0, при котором достигается наибольшая из возможных вероятностей, определяется как целое число на промежутке по формуле:
n∙p-q≤m_0≤n∙p+p
Для данного случая
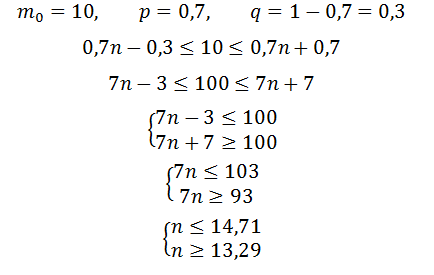
так как n – целое число, то n = 14
Ответ:n = 14