7. Вероятностные и статистические характеристики случайных величин.Генеральная совокупность - все возможные значения воображаемых наблюдений случайной величены, которые можно было бы сделать. 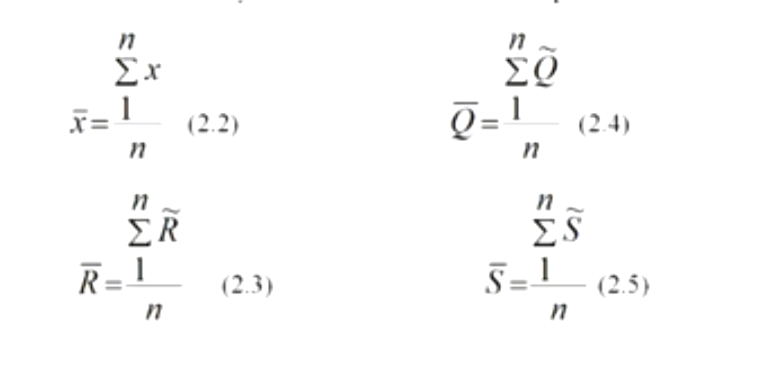На практике не возможно получить всю генеральную совокупность в следствие ее большого обьема.Выборка объема n – часть генеральной совокупности, включающая n наблюдения значений случайной величины.Математическое ожидание – среднее алгебраическое всех n наблюдаемых значений случайных величин в выборке объемом n:(тут можно прост одну формулу привести, это все примеры)Вероятность события – численная мера степени, объективной возможности этого события. А – событие; Р(А) – вероятность события ,,А” Пусть Х – конкретное значение случайно величины. Допускаем, нас будет интересовать событие заключается в том, в скольких случаях из всех n наблюдений, если n достаточно большое, будет обеспечиваться событие:Число которые с каким-то приближением тогда будет обозначать вероятность этого событияСобытие А заключается в том что конкретное значение случайны величины Х больше любого случайного значения.Функция распределения случайной величины F(x) F(x) – представляет собой вероятность события Х(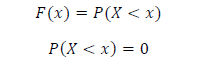вывод есть 45-ая минута 2-ой лекции)Плотность распределения случайной величины – первая производная функции распределения по х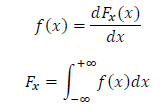Свойства:

1. 
   Плотность распределения – число всегда неотрицательное.
   
2. 
   
   

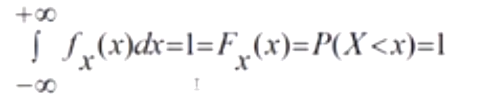
Для симметричной области измерения х всегда допустимо выражение:

---

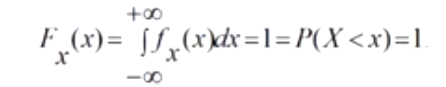
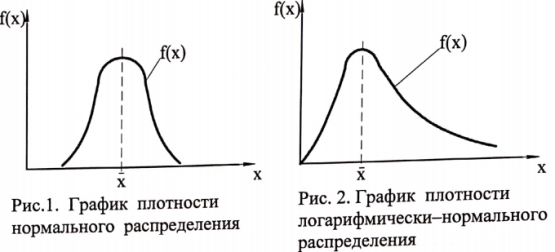
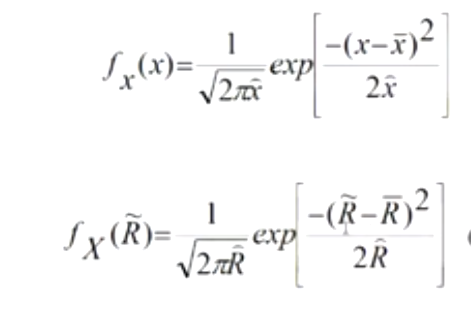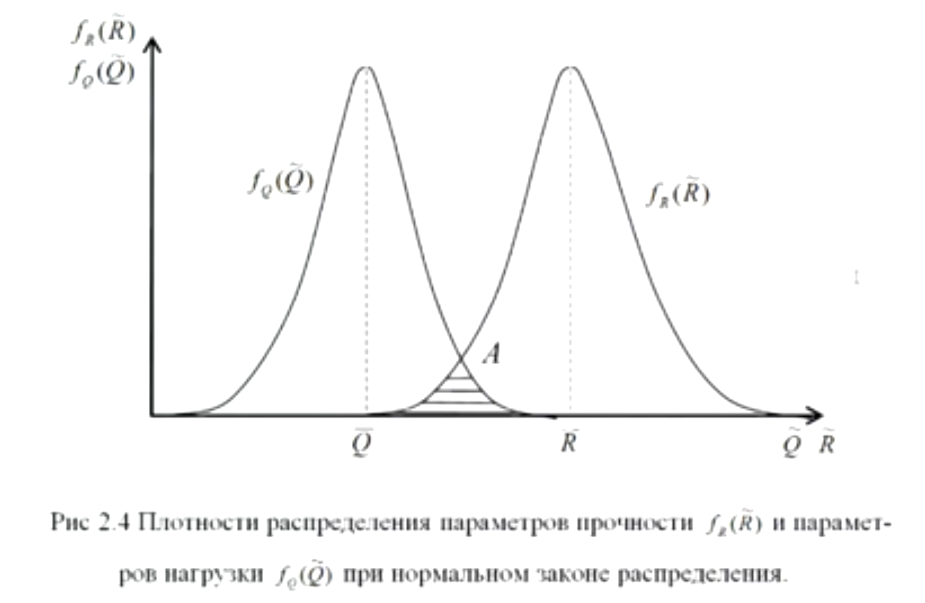
Если случайная величина может принимать любое значение от - ꝏ до + ꝏ, то всегда найдется случайное ее значение х, которое больше данного конкретного значения.Дополнительно расписано 1:04 2-ой лекцииПлотность распределения при нормальном законе распределения хˆ-дисперсия случайной величиныДисперсия случайной величины характеризует среднеквадратичное отклонение разброса значений случайных величины из выборки n относительно математическое ожидание 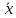при , 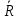или 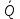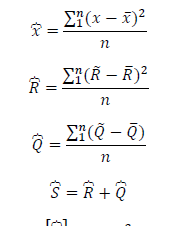Стандарт отклонения случайной величины ( стандартное отклонение случайной величины от математического ожидания)(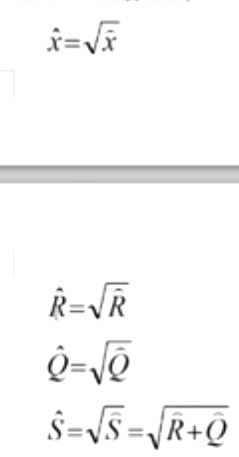Подробнее 1:24)Механический смысл плотности распределения – закон распределения проявления конкретных значений случайной величины8. Законы распределения случайных величин.Закон распред СВ – функция, описывающая поведение частоты проявления конкретных значений в области изменения СВ. Бывает для дискретной СВ и для непрерывной СВ. Для непрерывной СВ з-н распред-я это и есть та функция, которая получается после первой производной f(x)=dF(x)/dx. При нормальном з-не распред-я, з-н распр-я и плотность распред-я описываются з-ном Пуассона: 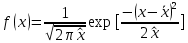. Логарифмичеки-нормальный з-н распред-я: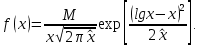

---

M – коэф-т перехода от десятич лгфм к натуральным. Также сущ-т з-ны Стьюдента и Гаусса.





9. Безотказность магистральных трубопроводов, определение вероятности отказа

Безотказное функционирование ТП, резервуаров и оборудования заключается в способности данной конструкции противостоять отказу в виде потери прочности или местные потери устойчивости оболочки в заданных условиях функции.

Оценка безотказность сводится к определению характеристики, количественное возможность разрушения или местные потери устойчивости с учетом изменчивости и случайного характера нагрузок и воздействий.

Таким образом, основное средство оценки безотказности – определение вероятности отказа или вероятности безотказности работы

Безотказность стенки трубы или резервуара, как конструкции, гарантируется на стадии проектирования расчетами на прочность устойчивость и по деформациям, которые задают необходимые соотношния между параметрами прочности и параметров нагрузки. Эти соотношения представляют неравенства, ограничивающие область безопасных состояний конструкции.

Вероятность отказа. Обозначают V

Это вероятность невыполнения неравенства .

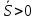Если выполняется- отказа не произойдет, если не выполняется- произойдёт.

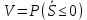– вер-ть отказа.

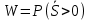- вер-ть безотказной работы.

Если V=0, то разрушение не произойдет ни при каких условиях. (на практике очень сложно достигнуть, только за счет больших экономических затрат)

В общем случае , при любом законе распределения случайных велечин, вероятность отказа:



при нормальном з-не распред-я:

Ф(γ) – интеграл вер-ти Гаусса. γ – хар-ка безотказности.

---

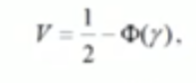
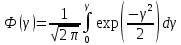
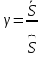
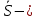мат ожидание запаса прочности 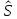- стандарт отклонения запаса прочности, как случайной велечины.Определение вероятности отказаВероятность отказа определяюи на стадии проектирования и на стадии эксплуатацииПолагаем, что G̃_прN >0;( G̃_iкц; G̃_iпр)

Порядок расчета

1. 
   Вычисляются мат ожидания параметров прочности, нагрузки и запаса прочности
   

2. 
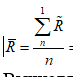
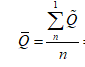
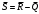
   Дисперсия параметров прочности и нагрузки
   

3. 
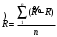
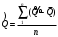
   Стандарт отклонения резерва прочности
   

4. 
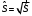
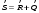
   Параметр безотказности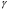
   

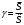
5. 
   Значение интеграла гаусса (по табл)
   

6. 
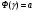
   Вероятность отказа
   

7. 
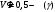
   Проверяется условие
   

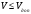
10. Регулирование вероятности отказа





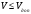
(формула 3.11 это )



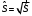Варианты- увеличить толщину стенки, уменьшить давление, использовать более прочную сталь, более однородную.


(было у прошлых годов хз что это)

11. Концентрация напряжений, теоретические коэффициенты концентраций напряжений на дефектах.

Эффект концентрации напряжений – в сечении с дефектом мех. напряжения скачком возрастают в сравнении с номинальным напряжением в бездефектном сварном шве. Причина - уменьшение рабочей площади поп. сечения и изменение геом. формы сварного шва. (не уверена что то, взято у прошлых лет)
Практически все сварные швы создают концентрацию напряжений вследствие несоответствия геометрических размеров шва, смещения кромок, овальности трубы, её угловатости, подрезов и т.д. Инженерная оценка напряженного состояния сварных соединений производится в рамках допустимости принципа суперпозиции, согласно которому общий коэффициент концентрации напряжений представляется в виде произведения коэффициента формы шва, геометрического отклонения, а также коэффициента, учитывающего наличие подреза (при наличии такового):


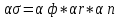
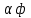– к-т формы шва, зависит от размеров шва

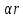– к-т, учитывающий геом. отклонения св. шва от нормы

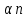– к-т подреза, учит. все внутренние размеры внут. дефектов и подрезов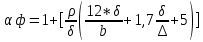



где 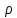– радиус перехода от металла шва к осн. металлу

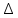- высота усиления св. шва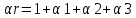





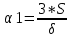
где S – поперечное смещение



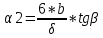
бетта – угловое смещение



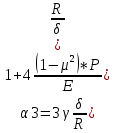
мю – к-т пуассона

R – радиус трубы

гамма – параметр овальности

P –раб давление

E – модуль упругости



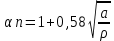
a – глубина подреза

ро – радиус в вершине подреза

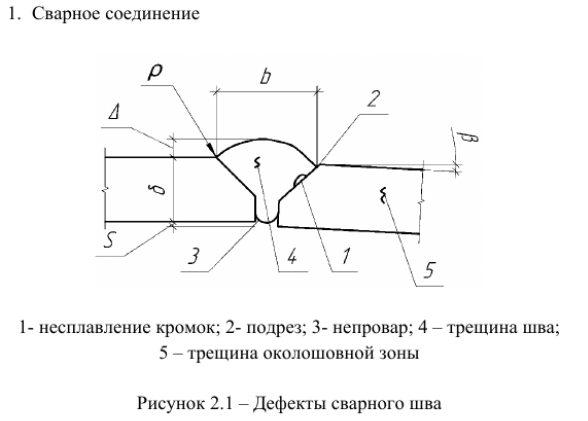
12. Дефекты сварных соединений, теоретические коэффициенты концентраций напряжений.

Группы дефектов:

1) геометрические отклонения при сборке сварного стыка

2) дефекты формы и размеров сварного шва;

3) внутренние дефекты сварного шва и околошовной зоны

(взято у прошлого года)


Практически все сварные швы создают концентрацию напряжений вследствие несоответствия геометрических размеров шва, смещения кромок, овальности трубы, её угловатости, подрезов и т.д. Инженерная оценка напряженного состояния сварных соединений производится в рамках допустимости принципа суперпозиции, согласно которому общий коэффициент концентрации напряжений представляется в виде произведения коэффициента формы шва, геометрического отклонения, а также коэффициента, учитывающего наличие подреза (при наличии такового):


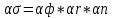
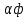– к-т формы шва, зависит от размеров шва

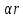– к-т, учитывающий геом. отклонения св. шва от нормы

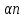– к-т подреза, учит. все внутренние размеры внут. дефектов и подрезов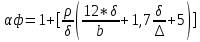



где 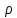– радиус перехода от металла шва к осн. металлу

- высота усиления св. шва





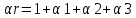
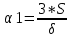
где S – поперечное смещение



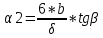
бетта – угловое смещение



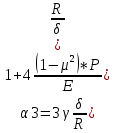
мю – к-т пуассона

R – радиус трубы

гамма – параметр овальности

P –раб давление

E – модуль упругости



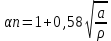
a – глубина подреза

ро – радиус в вершине подреза

---

Смотрите также файлы

• Урок 12 общее учение о болезни.docx

• Характеристика на ученика 5 класса Кабальникова Рустама.odt

• Главное управление Федеральной службы судебных приставов по Свердловской области осп кировского района г. Екатеринбурга.docx

• Статья 42. Порядок привлечения прокуроров к уголовной и административной ответственности.docx

• Изложите свою точку зрения, подкрепите примерами.docx