Файл: Курсовая работа по дисциплине Гидрогазодинамика Проверил Устинов Н. В.docx
Добавлен: 10.01.2024
Просмотров: 59
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
плотность жидкости; v – скорость движения потока до его остановки; с – скорость распространения ударной волны; Т – фаза ударной волны; 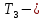 время закрывания задвижки.
время закрывания задвижки.
Максимально допустимое давление для данного трубопровода определяется с учетом допустимого напряжения стенок на разрыв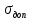 .
.
Разрывающее усилие, испытываемое стенками трубопровода под влиянием давления p, определяется по формуле
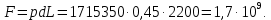
Это усилие воспринимается площадью сечения стенок трубопровода
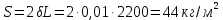
А растягивающее напряжение
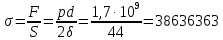
Отсюда искомое максимально допустимое давление для заданного трубопровода определяется по формуле
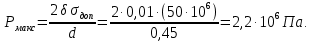
Минимально допустимое время закрывания задвижки определяем по формуле
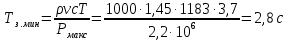
Задача № 2
Задание 2.1 Выполнить газодинамический расчет сопла Лаваля.
Провести газодинамический расчет сопла Лаваля (рис 5), обеспечиваюшего в расчетном режиме массовый расход кислорода G = 10 кг/с. параметры торможения: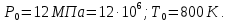 Скорость входа газа
Скорость входа газа 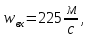 показатель адиабаты k = 1.41. Углы раствора сопла: дозвуковой части
показатель адиабаты k = 1.41. Углы раствора сопла: дозвуковой части 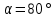 ; сверхзвуковой части
; сверхзвуковой части 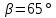 . Давление на срезе сопла
. Давление на срезе сопла 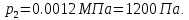
Требуется:
Определить, параметры газа в основных (входного, критического и выходного) и дополнительных сечениях 1,2, 3, 4 и построить графики зависимости P-?, T-?, W-?,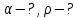 по длине сопла.
по длине сопла.
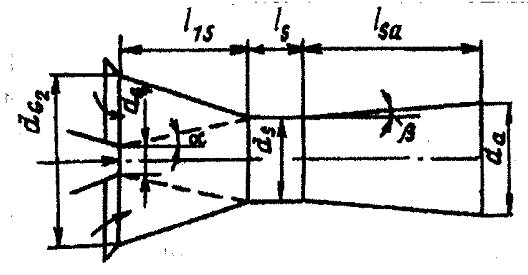
Рисунок 5
По мере движения газа по соплу (рис 5), его абсолютная температура Т и давление р снижаются, а скорость w возрастет (рис 6).
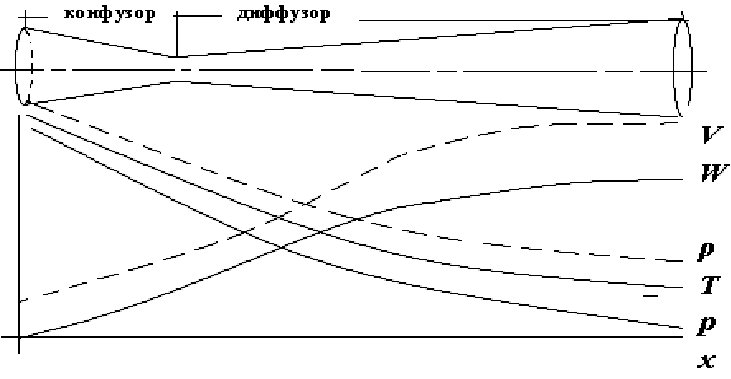
Рисунок 6
Решение
Газовая постоянная для кислорода R= 260 Дж/кг*К,
Из уравнения Менделеева – Клапейрона находим плотность газа при полной остановке:
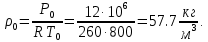
Находим скорость звука при полной остановке газа:
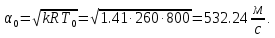
Где k – показатель адиабаты, равный 1,41 для двухатомного газа.
Определим скорость звука в критическом сечении:
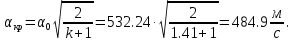
Максимальную скорость газового потока находим по формуле
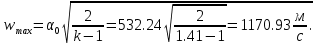
В критическом сечении коэффициент скорости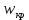 число Маха
число Маха 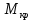 равны единице:
равны единице:
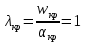 , откуда находим скорость газового потока в критическом сечении:
, откуда находим скорость газового потока в критическом сечении:
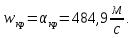
Используя газодинамическую функцию, находим температуру газа в критическом сечении:
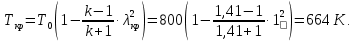
Рассчитаем давление газа в критическом сечении, используя газодинамическую функцию:
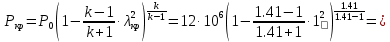
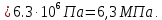
Найдем плотность газа в критическом сечении, используя газодинамическую функцию:
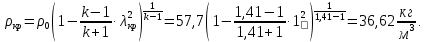
Из уравнения неразрывности потока находим площадь критического сечения:
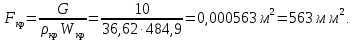
Находим диаметр критического сечения
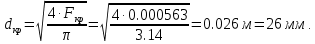
Находим коэффициент скорости во входном сечении
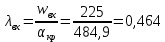
Используя газодинамическую функцию, находим температуру газа во входном сечении:
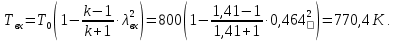
Рассчитаем давление газа в входном сечении, используя газодинамическую функцию:
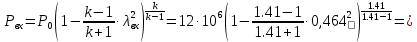
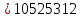 Па
Па
Найдем плотность газа в входном сечении, используя газодинамическую функцию:
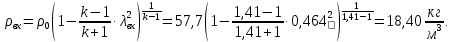
Из уравнения неразрывности потока находим площадь входного сечения:
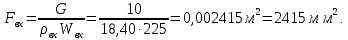
Находим диаметр входного сечения
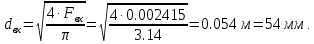
Вычисляем скорость звука во входном сечении:
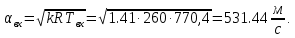
Определяем число Маха во входном сечении:
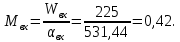
Используя газодинамическую функцию, находим коэффициент скорости в выходном сечении:
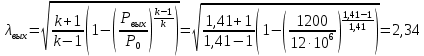
Где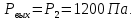
Используя газодинамическую функцию, находим температуру газа в выходном сечении:
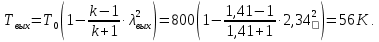
Рассчитаем давление газа в выходном сечении, используя газодинамическую функцию:
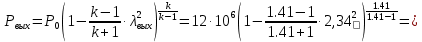
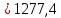 Па
Па
Найдем плотность газа в входном сечении, используя газодинамическую функцию:
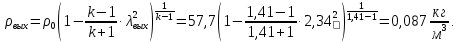
Определим скорость газового потока в выходном сечении:
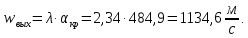
Из уравнения неразрывности потока находим площадь входного сечения:
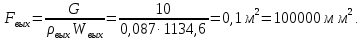
Находим диаметр выходного сечения
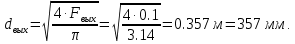
Вычисляем скорость звука во выходном сечении:
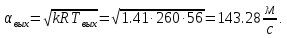
Определяем число Маха во выходном сечении:
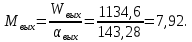
Определим длину суживающейся (дозвуковой) части сопла:
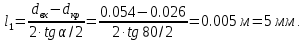
Находим длину расширяющейся (сверхзвуковой) части сопла:
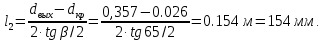
Вычисляем общую длину сопла:
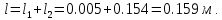
Задание 2.2 Определить параметры потока после прямого скачка уплотнения при течении воздуха по трубе.
Дано:
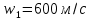 .
.
 .
.
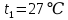 .
.
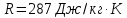 .
.
К = 1,41.
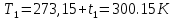 .
.
Прямой скачок уплотнения возникает только в сверхзвуковом потоке (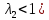 . Изменение параметров газа при переходе через скачок имеет вид:
. Изменение параметров газа при переходе через скачок имеет вид:
Изменения параметров газа при переходе через скачок имеют вид:
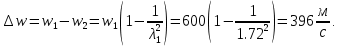
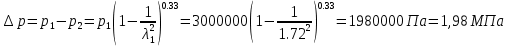
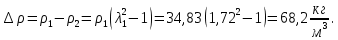
Где
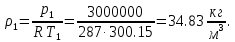
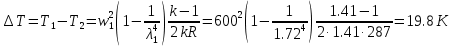
Где
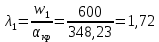
Критическая скорость звука может быть определена из отношения
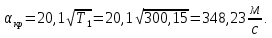
Параметры заторможенного потока находим, используя зависимости:
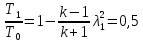
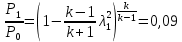
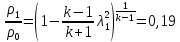
Где
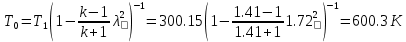
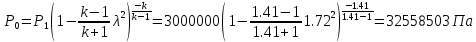
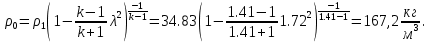
Список используемой литературы
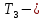 время закрывания задвижки.
время закрывания задвижки.Максимально допустимое давление для данного трубопровода определяется с учетом допустимого напряжения стенок на разрыв
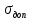 .
.Разрывающее усилие, испытываемое стенками трубопровода под влиянием давления p, определяется по формуле
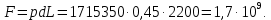
Это усилие воспринимается площадью сечения стенок трубопровода
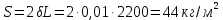
А растягивающее напряжение
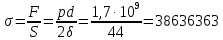
Отсюда искомое максимально допустимое давление для заданного трубопровода определяется по формуле
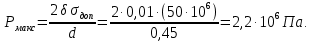
Минимально допустимое время закрывания задвижки определяем по формуле
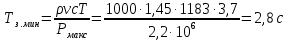
Задача № 2
Задание 2.1 Выполнить газодинамический расчет сопла Лаваля.
Провести газодинамический расчет сопла Лаваля (рис 5), обеспечиваюшего в расчетном режиме массовый расход кислорода G = 10 кг/с. параметры торможения:
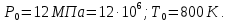 Скорость входа газа
Скорость входа газа 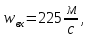 показатель адиабаты k = 1.41. Углы раствора сопла: дозвуковой части
показатель адиабаты k = 1.41. Углы раствора сопла: дозвуковой части 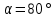 ; сверхзвуковой части
; сверхзвуковой части 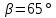 . Давление на срезе сопла
. Давление на срезе сопла 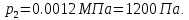
Требуется:
Определить, параметры газа в основных (входного, критического и выходного) и дополнительных сечениях 1,2, 3, 4 и построить графики зависимости P-?, T-?, W-?,
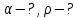 по длине сопла.
по длине сопла.
Рисунок 5
По мере движения газа по соплу (рис 5), его абсолютная температура Т и давление р снижаются, а скорость w возрастет (рис 6).

Рисунок 6
Решение
-
Расчет параметров газа в критическом сечении.
Газовая постоянная для кислорода R= 260 Дж/кг*К,
Из уравнения Менделеева – Клапейрона находим плотность газа при полной остановке:
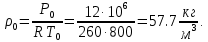
Находим скорость звука при полной остановке газа:
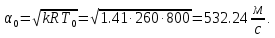
Где k – показатель адиабаты, равный 1,41 для двухатомного газа.
Определим скорость звука в критическом сечении:
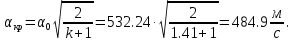
Максимальную скорость газового потока находим по формуле
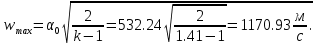
В критическом сечении коэффициент скорости
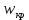 число Маха
число Маха 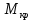 равны единице:
равны единице: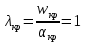 , откуда находим скорость газового потока в критическом сечении:
, откуда находим скорость газового потока в критическом сечении: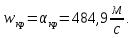
Используя газодинамическую функцию, находим температуру газа в критическом сечении:
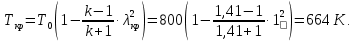
Рассчитаем давление газа в критическом сечении, используя газодинамическую функцию:
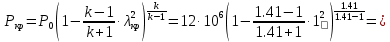
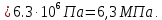
Найдем плотность газа в критическом сечении, используя газодинамическую функцию:
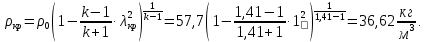
Из уравнения неразрывности потока находим площадь критического сечения:
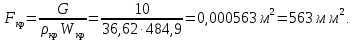
Находим диаметр критического сечения
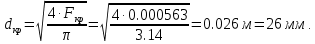
-
Расчет параметров газа во входном сечении.
Находим коэффициент скорости во входном сечении
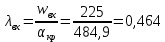
Используя газодинамическую функцию, находим температуру газа во входном сечении:
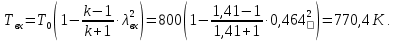
Рассчитаем давление газа в входном сечении, используя газодинамическую функцию:
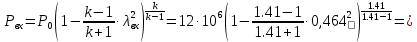
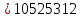 Па
ПаНайдем плотность газа в входном сечении, используя газодинамическую функцию:
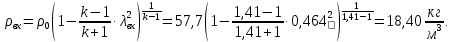
Из уравнения неразрывности потока находим площадь входного сечения:
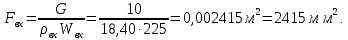
Находим диаметр входного сечения
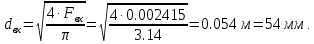
Вычисляем скорость звука во входном сечении:
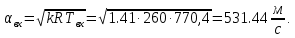
Определяем число Маха во входном сечении:
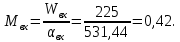
-
Расчет параметров газа в выходном сечении.
Используя газодинамическую функцию, находим коэффициент скорости в выходном сечении:
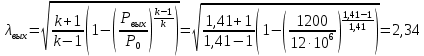
Где
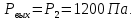
Используя газодинамическую функцию, находим температуру газа в выходном сечении:
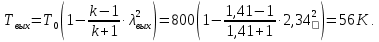
Рассчитаем давление газа в выходном сечении, используя газодинамическую функцию:
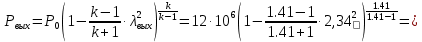
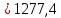 Па
ПаНайдем плотность газа в входном сечении, используя газодинамическую функцию:
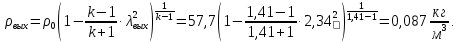
Определим скорость газового потока в выходном сечении:
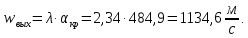
Из уравнения неразрывности потока находим площадь входного сечения:
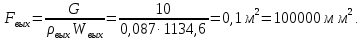
Находим диаметр выходного сечения
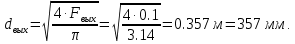
Вычисляем скорость звука во выходном сечении:
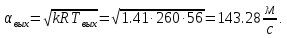
Определяем число Маха во выходном сечении:
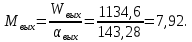
-
Геометрический профиль сопла.
Определим длину суживающейся (дозвуковой) части сопла:
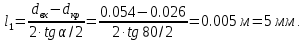
Находим длину расширяющейся (сверхзвуковой) части сопла:
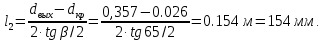
Вычисляем общую длину сопла:
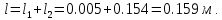
Задание 2.2 Определить параметры потока после прямого скачка уплотнения при течении воздуха по трубе.
Дано:
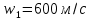 .
. .
.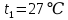 .
.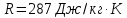 .
.К = 1,41.
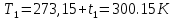 .
.-
Определить скорость потока после прямого скачка уплотнения. -
Определить параметры заторможенного потока.
Прямой скачок уплотнения возникает только в сверхзвуковом потоке (
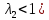 . Изменение параметров газа при переходе через скачок имеет вид:
. Изменение параметров газа при переходе через скачок имеет вид:Изменения параметров газа при переходе через скачок имеют вид:
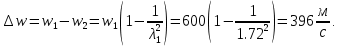
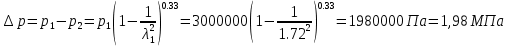
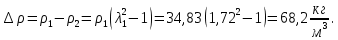
Где
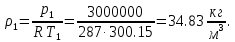
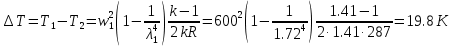
Где
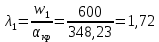
Критическая скорость звука может быть определена из отношения
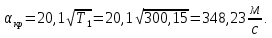
Параметры заторможенного потока находим, используя зависимости:
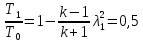
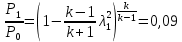
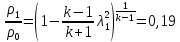
Где
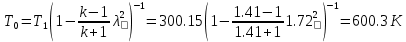
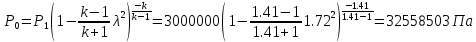
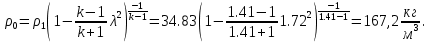




Список используемой литературы
-
Штеренлихт А.Б, Гидравлика. Учебник, - М.: Колосс, 2009. -
Кузьминский Р.С. Гидрогазодинамика. Учебное пособие. – М.: МИИТ, 2011. -
Давидсон В.Е. Основы гидрогазодинамики в примерах и задачах. Учебное пособие. – М.: Издательский центр «Академия», 2008. -
Бекнев В.С. и др. Сборник задач и упражнений по газовой динамике. – М.: Машиностроение, 1992.