ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тверской государственный технический университет»
(ТвГТУ)
Факультет информационных технологий
Кафедра «Информационные системы»
Контрольная работа
ПРЕДМЕТ: ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Выполнил(-а):
Студент 2 курса
Группа Б.ИСТ.РВС.21.52
Направление подготовки
бакалавров: Информационные системы и технологии
Проверил: к.т.н., доцент Ветров А.Н.
Тверь, 2023
5. Брошены две игральные кости. Найти вероятности следующих событий:
а) сумма выпавших очков равна семи;
б) сумма выпавших очков равна восьми, а разность — четырем;
в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем;
г) сумма выпавших очков равна пяти, а произведение — четырем
Общее число возможных элементарных исходов испытания равно 6*6 = 36.
а) сумма выпавших очков равна семи;
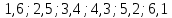
m= 6, n=36
Вероятность равна 6/36 = 1/6
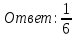
б) сумма выпавших очков равна восьми, а разность — четырем;
x – первый кубик, y- второй кубик
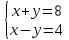
x = 8 – y
8 –y –y = 4
1. y = 2;
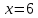
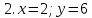
Вероятность равна 2/36 = 1/18
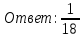
в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем;
Событие С = {сумма выпавших очков равна 8, если известно, что их разность равна 4}
Событие A = {сумма выпавших очков равна 8}
Событие B = {разность выпавших очков равна 4}
По формуле условной вероятности: P(A|B) = P(A·B) / P(B), то есть:
P(B): m = {(1, 5); (2, 6); (5, 1); (6, 2)} ⇒ P(B) = 4/36 = 1/9
P(A·B) = {сумма выпавших очков равна 8 и их разность равна 4}: {(2, 6); (6, 2)} ⇒ P(A·B) = 2/36 = 1/18
Тогда: P(D) = P(A·B) / P(B) = (1/18) · 9 = 0,5
Ответ: 0,5
г) сумма выпавших очков равна пяти, а произведение — четырем
x – первый кубик, y- второй кубик
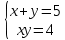
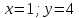
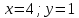
Вероятность равна 2/36 = 1/18
7. Монета брошена два раза. Найти вероятность того, что, хотя бы один раз появится «герб».
Г - герб, Р – решка. Возможные исходы: ГГ, ГР, РГ, РР. 4 элементарных исхода. Те, где присутствует герб 3. m=3, n=4
P=m/n=3/4.
Ответ: 3/4
12. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Количество всех возможных исходов равно:
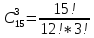= 455Количество благоприятных исходов равно:
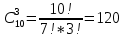
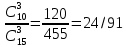
Ответ: 24/91
18. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
Количество всех возможных исходов равно:
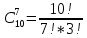= 455Количество благоприятных исходов равно:
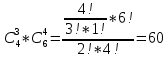
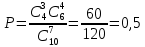
Ответ: 0,5
51. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго—0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
В событии 2 случая:
1. Попадает первый стрелок, а второй стрелок промахивается. По правилу умножения вероятностей (первый и второй стрелок независимы) получаем, 0,7*(1-0,8)=0,14.
2. Попадает второй стрелок, а первый стрелок промахивается. По правилу умножения вероятностей получаем (1-0,7)*0,8=0,24.
Тогда вероятность искомого события равна сумме вероятностей этих двух случаев 0,14+0,24=0,38.
Ответ: 0,38
52. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.
Пусть вероятность попасть из первого орудия - p1, вероятность промаха - q1.
Вероятность попасть в цель для второго орудия равна p2 = 0,8;
Вероятность промаха для второго орудия:
q2 = 1 - p2 = 1 - 0,8 = 0,2;
Вероятность, что будет одна пробоина, равна сумме вероятностей того, что попало первое орудие, а второе промахнулось или что попало второе, а первое сделало промах.
P = p1 · q2 + p2 · q1;
0,38 = p1 · 0,2 + 0,8 · (1 - p1);
0,38 = 0,8 - 0,6 · p1;
0,6 · p1 = 0,42;
p1 = 0,7;
Ответ: Вероятность поражения цели одним выстрелом из первого орудия p1 = 0,7.
59. Брошены три игральные кости. Найти вероятности следующих событий:
а) на двух выпавших гранях появится одно очко, а на третьей грани—другое число очков;
б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани—другое число очков;
в) на всех выпавших гранях появится разное число очков.
а)
Выбрать 2 кости (кубика) из трех можно
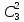= 3!/(2!*1!) = 3 способами.Вероятность выпадения одного очка равна 1/6, а выпадение не "1" равна 5/6.
По формуле Бернулли: Р= 3*(1/6)2*(5/6) = 3*1/36 *5/6 = 5/72
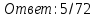
б)
Вероятность выпадения двух двоек или двух троек и т.д. такая же,
как и вероятность выпадения двух единиц. Таких вариантов 6.
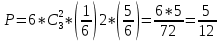
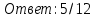
в) Поскольку бросается 3 кости, то всего возможно 6*6*6 = 216 различных комбинаций их выпадения. Число очков на каждой кости может быть от 1 до 6, всего 6 вариантов. Поскольку все три числа очков разные, то воспользуемся формулой для размещения без повторений:
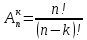, n=6, k=3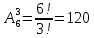
P = 120/216 = 5/9
Ответ: 5/9
81. Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Вероятности отказов для каждого из приборов:
p1 = 0,05;
p2 = 0,08;
Вероятности безотказной работы приборов:
q1 = 1 - p1 = 1 - 0,05 = 0,95.
q2 = 1 - p2 = 1 - 0,08 = 0,92.
Вероятность, что оба прибора будут работать безотказно:
P = q1 · q2 = 0,95 · 0,92 = 0,874.
Вероятность противоположного события такого, что откажет хотя бы один прибор:
P` = 1 - P = 1 - 0,874 = 0,126.
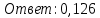
90. В урну, содержащую n шаров, опущен белый шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Пусть в урне первоначально m белых шаров. После того, как в урну положили еще один белый шар, то вероятность достать белый шар стала (m+1)/(n+1).
Вероятность того, что в урне m белых шаров, равна 1/(n+1). (от 0 до n, всего n+1 вариант).
Тогда по формуле полной вероятности получаем, что искомая вероятность равна:
P(A) =
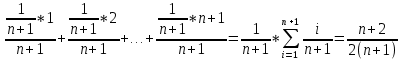
Ответ:
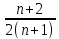
94. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
Пусть:
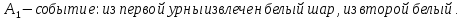
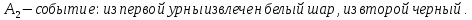
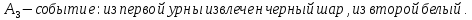
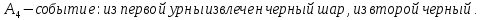
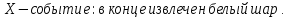
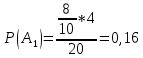
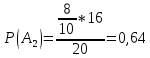
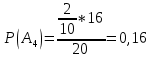
Вероятность события X находим по формуле полной вероятности
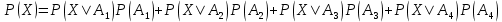
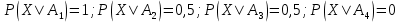
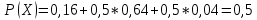
Ответ: 0,5
98. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
Пусть
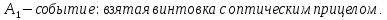
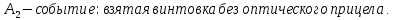
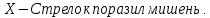
Находим вероятность того, что винтовка взята с оптическим прицелом.
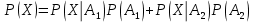
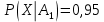
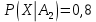
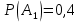
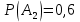
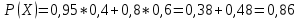
Далее применяем формулу Байеса.
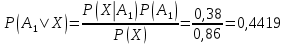
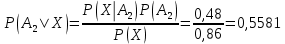
Ответ: Вероятнее, что стрелок стрелял из винтовки без оптического прицела.
112. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет:
а) менее двух раз;
б) не менее двух раз.
Используем формулу Бернулли.
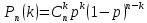
а)
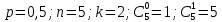
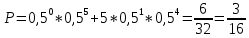
Ответ:
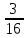
б) Данное событие является обратным к событию пункта а)
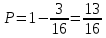
Ответ:
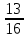
167. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
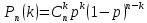
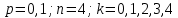
| k | 0 | 1 | 2 | 3 | 4 |
| P(X = k) | 0,6561 | 0,0729 | 0,0081 | 0,0009 | 0,0001 |